
解:摩擦力的元功 d4=fcosadx=-(1+x)dx 从x=0到x=L摩擦力共做功 d=M=小+ -x+26=-40+2
解: 摩擦力的元功 d cos d (1 )d A f x x x = = − + α =π 从 x x L = = 0到 摩擦力共做功 0 (1 )d L L A dA x x = = − + 2 0 1 ( ) (1 ) 2 2 x L = − + = − + x L L

功的计算 ()分析质点受力情况,确定力随位置变化的关系; (2)写出元功的表达式,选定积分变量; (3)确定积分限进行积分,求出总功。 F-Fi+Fj A=∫F.+∫F, dr dxi +dyj 例1.设作用在质量为2kg的物体上的力F=6t(N)。如果物体由静 止出发沿直线运动,问在头2s时间内,这个力对物体所作的功。 解:按功的定义式计算功,必须首先求出力和位移的关系式。 根据牛顿第二定律F=m可知物体的加速度为a=Fm=6t/2=3t 所以 dv=adt=3tdt dx vdt 1.5t'dt dw=「3tdt=1.5t2 0 力所作的功为A∫F=∫61,5dh=j9rh=36J
•功的计算 (1)分析质点受力情况,确定力随位置变化的关系; (2)写出元功的表达式,选定积分变量; (3)确定积分限进行积分,求出总功。 dr dxi dyj F F i F j x y = + = + A F dx + F dy = x y 例1.设作用在质量为2kg的物体上的力F =6t(N)。如果物体由静 止出发沿直线运动,问在头2s时间内,这个力对物体所作的功。 解:按功的定义式计算功,必须首先求出力和位移的关系式。 根据牛顿第二定律F=ma可知物体的加速度为 a=F/m=6t/2=3t 所以 dv=adt=3tdt 2 0 0 dv 3tdt 1.5t v t = = dx vdt t dt 2 = = 1.5 A Fdx 6t 1.5t dt 9t dt 36J 2 0 2 3 = = = = 力所作的功为
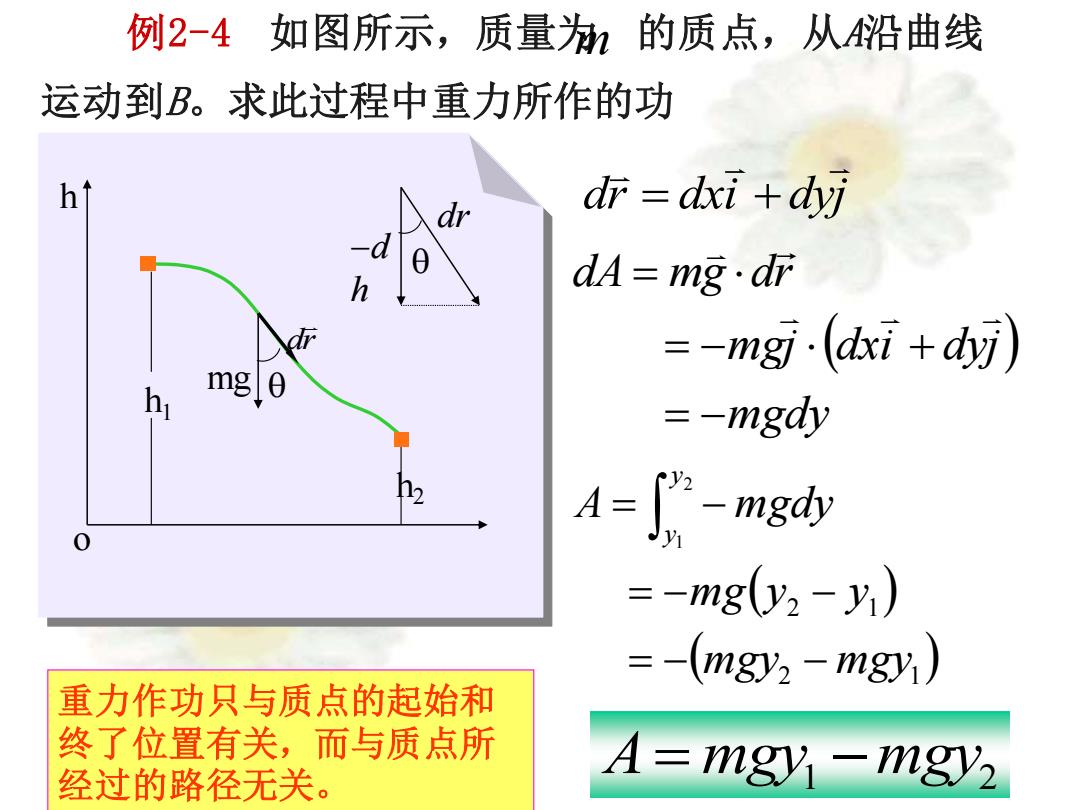
例2-4如图所示,质量为机的质点,从沿曲线 运动到B。求此过程中重力所作的功 h dr dr dxi +dyj h dA mg.dr =-mg·(aki+dj) mg 0 --mgdy A=-mgdy =-mg(y2-y) =-(mgy2-mg) 重力作功只与质点的起始和 终了位置有关,而与质点所 经过的路径无关。 A-mgy-mgy2
dr dxi dyj = + ( ) mgdy mgj dxi dyj dA mg dr = − = − + = ( ) ( ) 2 1 2 1 2 1 mgy mgy mg y y A mgdy y y = − − = − − = − A= mgy1 −mgy2 重力作功只与质点的起始和 终了位置有关,而与质点所 经过的路径无关。 o h h1 h2 dr mg q −d h dr q 例2-4 如图所示,质量为 的质点,从A沿曲线 运动到B。求此过程中重力所作的功 m

例2-5弹簧一端固定于墙上,另一端系一物体。 取弹簧无形变时物体所在位置为原点,弹簧伸长方向为 Ox轴的正方向,如图所示。拉伸或压缩弹簧时,作用于 物体的弹力为 f=-kx 在上式中,飞是弹簧的劲度系数,x是物体位置 的坐标。负号表示作用于物体的弹性力恒指向平衡位置 (原点)。计算物体从x,移动到X2过程中弹力所作的 功。 WWAM m x x+dx
例2-5 弹簧一端固定于墙上,另一端系一物体。 取弹簧无形变时物体所在位置为原点,弹簧伸长方向为 Ox轴的正方向,如图所示。拉伸或压缩弹簧时,作用于 物体的弹力为 f = −kx 在上式中, 是弹簧的劲度系数, 是物体位置 的坐标。负号表示作用于物体的弹性力恒指向平衡位置 (原点)。计算物体从 移动到 过程中弹力所作的 功。 k x o m f x x+dx k 2 x x 1 x
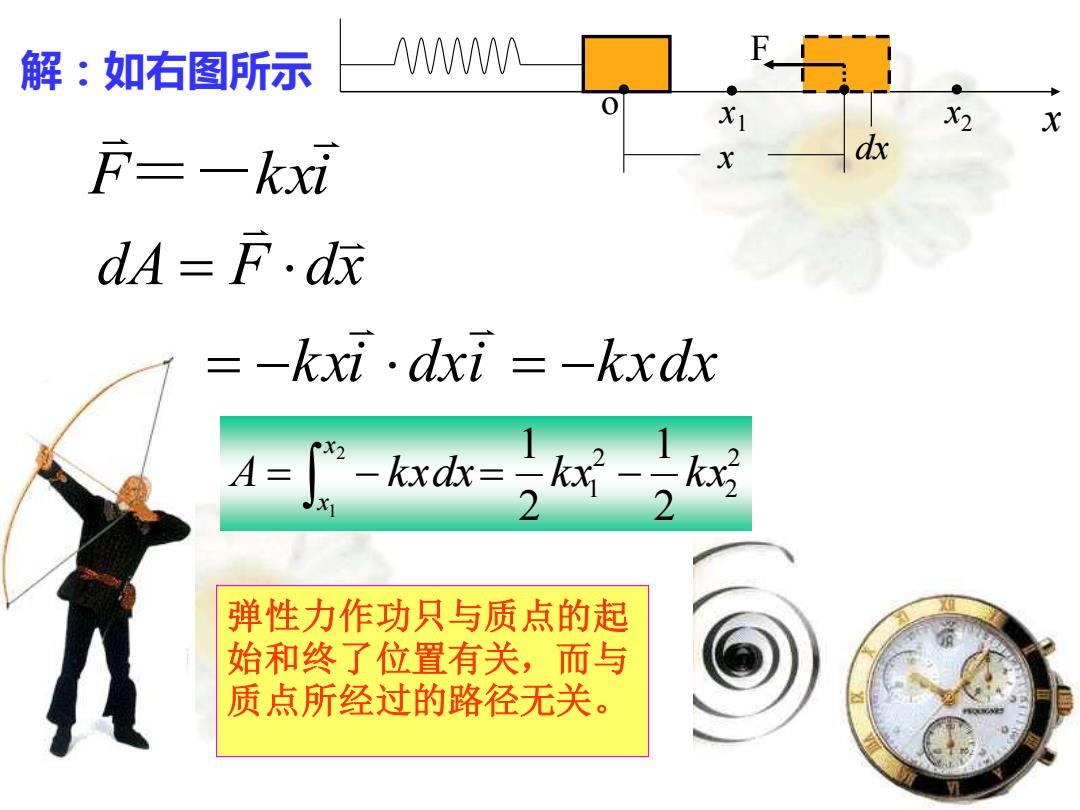
解:如右图所示 M X2 X F=-kxi dx dA=F.dx =-kxi·dxi=-kxdx A=小-k=然- 2 弹性力作功只与质点的起 始和终了位置有关,而与 质点所经过的路径无关
解:如右图所示 F k xi =- k xi dxi kxdx dA F dx = − = − = 2 2 2 1 2 1 2 2 1 1 A kxdx k x k x x x = − = − 弹性力作功只与质点的起 始和终了位置有关,而与 质点所经过的路径无关。 o x x1 dx F x2 x