
·32· 电力系统分析题解 号Ba=号A号=0.01852×器=0,01235 K=X号=0.4854×品-0.2541 号Ba=Ba号=0.01852×1 70 =0.0108 (2)计算各支路导纳。 0=x=-j0.23-j4.3478 1 1 =x2-j0.28-j3.7514 w-k=-j0.105=-j9.524 w一成。=-6a=-4762 1 1 为1=x=-j0.43554=-2.296 s=x2-j0.2904=-j3.44 x。-j0.25和=-3.936 yw=j2Ba+j2Be=j(0.01852+0.01235)=j0.03087 yo=j(2Ba+号Ba)=j0.01852+0.0108)=j0.02932 =j(B+2Ba)=j(0.01235+0.0108)=j0.02315 (3)计算导纳矩阵元素 (a)对角元 Y-yo+y1a=-j4.3478-j9.524=-j13.872 Ya=ym十3y24=-j3.5714-j4.762=-j8.333 Y3=y0+y31+y4十y35

1 第四章电力网络的数学模型 ·33· =j0.03087-j9.524-j2.296-j3.444=-j15.233 Y4=yo十y42十y43+y4s =j0.02932-j4.762-j2.296-j3.936=-10.965 Y5=3ys0十3+y5 =j0.02315-j3.444-j3.936=-j7.357 (b)非对角元 Y2=Y21=0.0,Y3=Y1=-y1s=j9.524 Y14=Y41=0.0,Ys=Y61=0.0 Y4=Y2=-y4=j4.762 Y4=Y4a=一4=j2.296,Y6=Y38=一3y%s=j3.444 Y45=Y4=一y4s=j3.936 导纳矩阵如下 -j13.8720.0j9.524 0.0 0.0 0.0 -j8.3330.0 j4.762 0.0 Y=j9.524 0.0 -j15.233j2.296 j3.444 0.0 j4.762j2.296 -j10.965 j3.936 10.0 0.0 3.444 j3.936 -j7.357 42对于题图4-1所示电力系统,试就下列两种情况分别修 改节点导纳矩阵:(1)节点5发生三相短路,(2)线路L3中点发生 三相短路。 解(1)因为在节点5发生三相短路,相当于节点5电位为 零,因此将原Y矩阵划去第5行和第5列,矩阵降为4阶,其余元 素不变。 (2)把线路L3分成两半,作成两个Ⅱ型等值电路,线路电抗 减少一半,其支路导纳增大一倍,线路并联电纳则减小一半,并且 分别成为节点4、5的对地导纳支路,因而节点4、5之间已无直接 联系。节点导纳矩阵的阶数不变,应修改的元素为 Y'w=Yu十y4-iBa

·34· 电力系统分析题解 =-j10.965-j3.936-j0.0108=-j14.906 Y'5=Y5十y45-j之Ba =-j7.357-j3.936-j0.0108=-j11.298 Y”46=Y'4=0.0 其余元素不变。 43在题图43的网络图中,已给出支路阻抗的标么值和节 点编号,试用支路追加法求节点阻抗矩阵。 3> 1 1+3 02 -j10 题图434节点网络 解先追加树支。 (1)追加0-1支路:Z1=1o=j10。 (2)追加1-2支路,矩阵增加一阶,为二阶矩阵,其元素为 Z1=-j10,Z2=Z2a=-j10 Z2=Z,+12=-j10+1+j3=1-j7 (3)追加1-3支路,矩阵增加一阶为三阶矩阵,原二阶矩阵各 元素不变,新增元素为 Z13=231=Z11=-j10,Z23=Z32=Z1=-j10 Z33=Z1+x1w=j10十j1=一j9 (4)追加1-4支路,矩阵又增加一阶,为四阶矩阵,原三阶矩阵 元素不变,新增元素为

第四章电力网络的数学模型 ·35· Z14=Z41=Z1=-j10 Z24-Z42=Z1=-j10 Z34=Z4=Z1=-j10 24=Z11十z14-j10+j2=-j8 (5)追加连支3-4支路,矩阵阶数不变。根据网络的结构特 点,单独在节点1(或节点2)上注入电流时,连支3-4的接入不会 改变网络中原有的电流和电压分布。因此,阻抗矩阵中的第1、2 行和第1、2列的全部元素都不必修改。需要修改的只是第3、4行 与第3、4列交叉处的4个元素,其修改如下 (23-Z4)(Z一Z43 Z=Z332n +Zu-2Zx+zm =-j9-二i8+i026i9ti192-j9.167 -j9-j8+2×j10+j3 ZM=Z4-0-2)(34-2u Z33+Z44一2Z34+之34 =-j8-二0828+i设=-j8.67 -j9-j8+2×j10+j3 (Z3-Z4)(Z4-Z4) 2=Zw=Z-Z0+Z4-2Z+4 =-j10-二i8±i028+i82-j9.67 -j9-j8+2×j10+j3 用支路追加法求得的节点阻抗矩阵如下 -10 -j10 -j10 -j10 1-j7 一j10 -j10 Z= -10 -j10 -j9.167 -j9.667 -j0 -j10 -j9.667 -j8.667 4-43节点网络如题图4-4所示,各支路阻抗标么值已在图 中注明。试根据节点导纳矩阵和节点阻抗矩阵元素的物理意义计 算各矩阵元素。 解(1)求各支路导纳
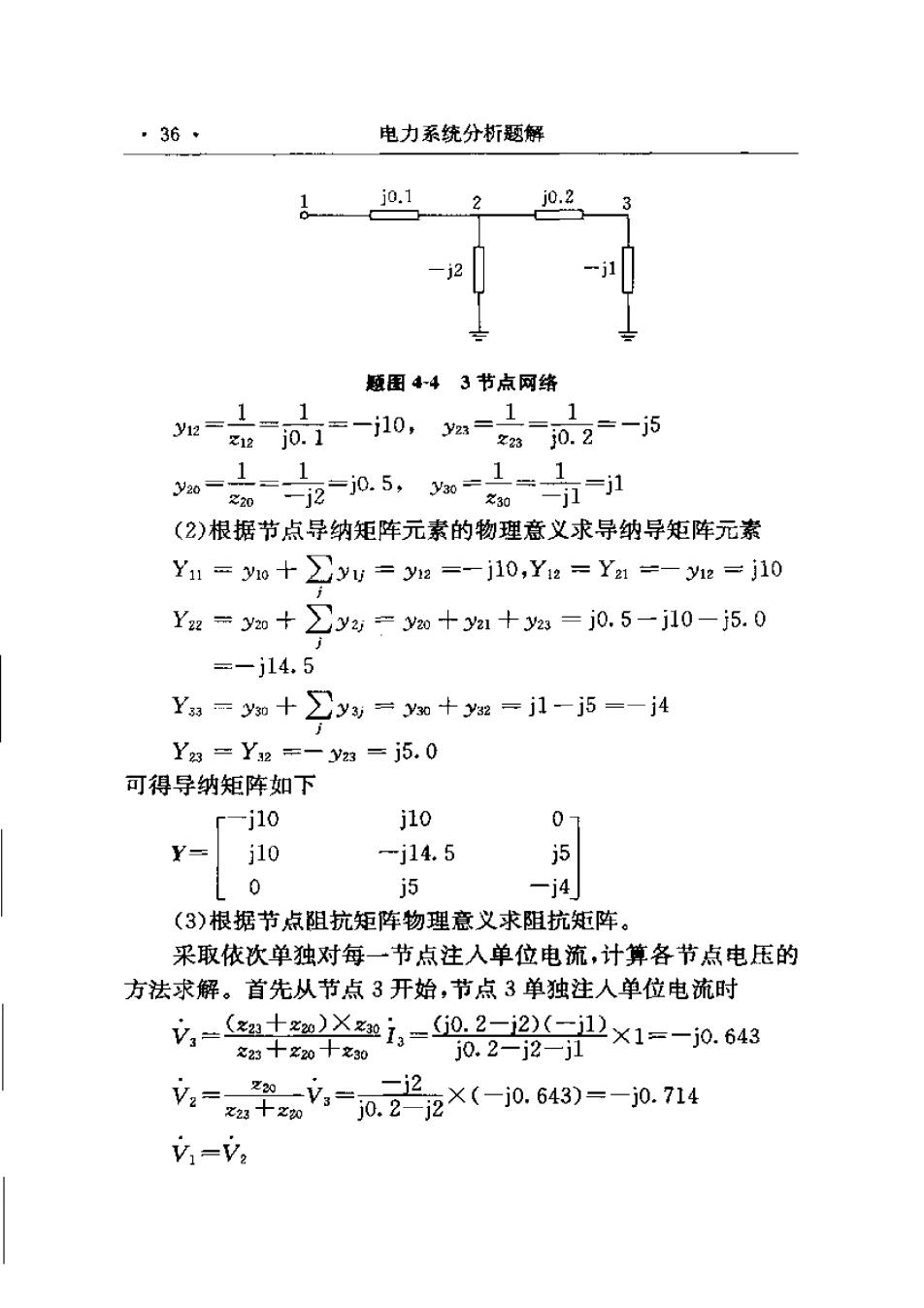
·36· 电力系统分析题解 c01 2 j0.2 -2 题围图443节点网络 1 1 y12=1 1 (2)根据节点导纳矩阵元素的物理意义求导纳导矩阵元素 Y1=o十∑yy=ya=-j10,Y2=Ya=-1e=j10 Y2=ym+∑y2=y0+y1+y23=j0.5-j10-j5.0 =-j14.5 Ya=y知+∑y=y知+y知=j1-j5=-j4 Y3=Y2=-y3=j5.0 可得导纳矩阵如下 「-j10 j10 07 Y=j10 -j14.5 5 0 j5 -j4 (3)根据节点阻抗矩阵物理意义求阻抗矩阵。 采取依次单独对每一节点注人单位电流,计算各节点电压的 方法求解。首先从节点3开始,节点3单独注人单位电流时 ,-ga十i。-0222卫×1=-j0.643 228十2g0十30 j0.2-j2-j1 -j2 7a竿z,=0,22×(-j0.643)=-0.714 V1=V2