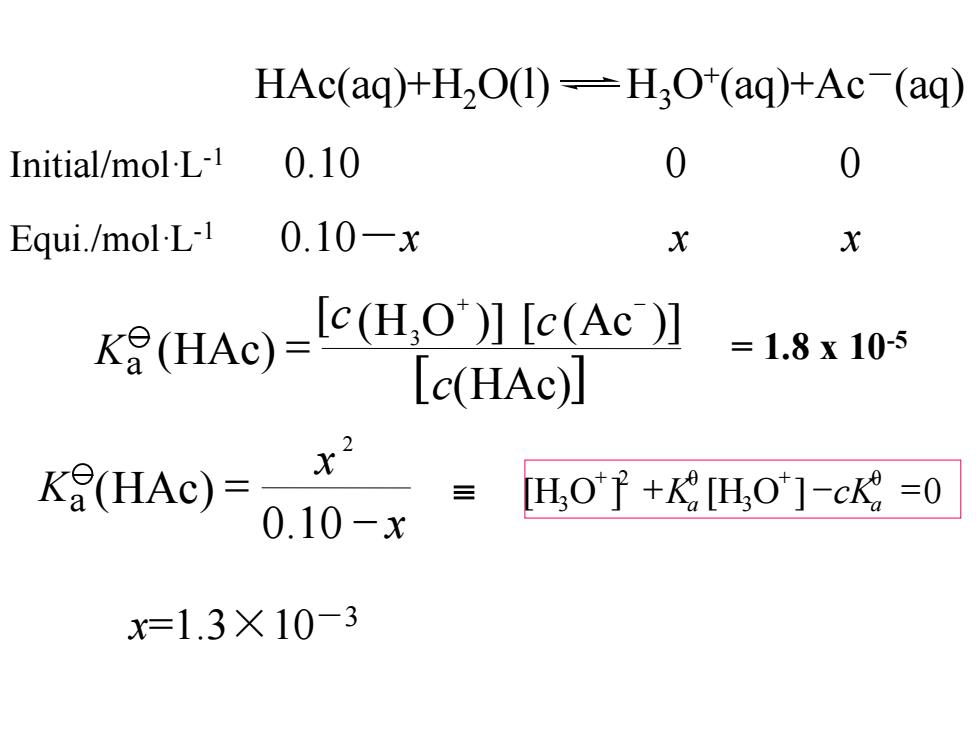
HAc(aq)+H2O(1)-H3O(aq)+Ac (aq) Initial/mol-L-1 0.10 Equi./mol-L-1 0.10-x x X kAe-cuQl6Ac升 =1.8x105 Lc(HAc)] K(HAc)= x .10-x H,O子+H,O]-ck=0 x=1.3×10-3
Initial/mol·L-1 0.10 0 0 Equi./mol·L-1 0.10-x x x x=1.3×10-3 HAc(aq)+H2O(l) H3O+ (aq)+Ac-(aq) [ (HAc)] (H O )] (Ac )] (HAc) 3 c [c [c + - K = a 0.10 x x (HAc) 2 - K = a = 1.8 x 10-5 + - = + + [H O ] [H O ] 0 θ 3 2 θ 3 a a K cK

cH30+)=c(Ac-)=1.3X10-3molL1 c(HAc)=(0.10-1.3×10-3)molL≈0.10molL1 K=c{(H3O)}{c(OH-)} c(0H-)=7.7×10-12molL1 pH=-lgc(H,O)}=2.89 percent ionizaton(a解离度 ionized concentration = x100%=c0-cgx100% original concentration Co 1.3×103 a(HAc)= ×100%=1.3% 0.10
percent ionizaton (a) 解离度 c(H3O+ ) = c(Ac-) = 1.3×10-3 mol·L-1 c(HAc)=(0.10-1.3×10-3 )mol·L-1≈0.10mol·L-1 c(OH-) =7.7×10-12 mol·L-1 pH = -lg{ (H3O )}= 2.89 + c =c{(H3O+ KW )}{c(OH-)} 100% 1.3% 0.10 1.3 10 3 = = - 醋酸的解离度 (HAc)α ionized concentration original concentration = x 100% = c0 - ceq c0 x 100%

The relationship between K,pH and a: If we ignore ionization of H2O,pH can be calculated simply when the value of a of an acid is given, HA(aq)=H(aq)+A(aq) Initial C 0 Equi. c-ca ca ca2 1-0x a<1021-a≈1 KHA) K(HA)=ca2 a=c) Dilution law(稀释定律):K,is a constant at a specified temperature,and a value increases when the solution of a weak electrolyte is diluted
The relationship between Ka , pH and α: HA(aq) H+ (aq) + A-(aq) Equi. c– cα cα cα Initial c 0 0 Dilution law(稀释定律):Ka is a constant at a specified temperature, and α value increases when the solution of a weak electrolyte is diluted.。 1 0 1 1 2 - - - = 1 2 a c K 当 a (HA) 1 0-4 时, c K { } 2 Ka (HA)= c {c} Ka (HA) = If we ignore ionization of H2O, pH can be calculated simply when the value of of an acid is given, ? when

2.Equilibrium of ionization for monoprotic bases: (1)calculation of pH of weak monoprotic bases with a given percent ionizaton (a) e.g.:A 0.200mol-L-1 solution of ammonia is ionized at 25C with a=0.95%.Calculate c(OH),the pH and ionization constant of the ammonia solution (ignore H,O's ionization) Answer:NH,(aq)+H,O(1)-NH;(aq)+OH(aq) Co 0.200 0 0 Ceq 0.200(1-0.95%) 0.200×0.95%0.200×0.95 c(0H)=0.200×0.95%=1.9×103 pH=14-p0H=14-(-lg1.9×10)=11.27
c0 0.200 0 0 3 pH 14 pOH 14 ( lg1.9 10 ) 11.27 - = - = - - × = 3 (OH ) 0.200 0.95% 1.9 10 - - c = × = × 2. Equilibrium of ionization for monoprotic bases: (1) calculation of pH of weak monoprotic bases with a given percent ionizaton (a) NH (aq) H O(l) NH (aq) OH (aq) 3 2 4 + - Answer: + + ceq 0.200(1– 0.95%) 0.200×0.95% 0.200×0.95% e.g.:A 0.200mol·L-1 solution of ammonia is ionized at 25℃ with a = 0.95%. Calculate c(OH-), the pH and ionization constant of the ammonia solution (ignore H2O’s ionization)

(NH)=(NH:)C(OH)_ (1.9×103)2 =1.8×10 c(NH,) 0.200-1.9X103 (2)calculation of pH of weak monoprotic bases B(aq)+H2O(1)=BH(aq)+OH-(aq) [BH+JOH-] K(B)=- [B] (NH3 +H2O=NH+OH)
(2) calculation of pH of weak monoprotic bases B(aq) + H2O(l) BH+ (aq) + OH- (aq) Kb (B) = [BH+ ][OH- ] [B] (NH3 + H2O NH4 + + OH- ) 5 1.8 10- 3 = × 3 2 3 4 3 0.200 1.9 10 (1.9 10 ) (NH ) (NH ) (OH ) (NH ) - + - - - × × = = c c c Kb