
正态分布 正态分布(normal distribution)也叫高斯分布 (Gaussian distribution),是最常见、最重要的一 种连续型分布。 一、正态分布的数学形式 二、标准正态分布 三、曲线下面积 四、正态性检验 五、正态分布的应用 6
正态分布(normal distribution)也叫高斯分布 (Gaussian distribution),是最常见、最重要的一 种连续型分布。 一、正态分布的数学形式 二、标准正态分布 三、曲线下面积 四、正态性检验 五、正态分布的应用 正态分布 6

一,正态分布的数学形式 1 -(x-0)2 f(x)= (22) gN2π ©)=随机变量X的频数, 称为概率密度函数 f() (probability density function) σ2=总体方差,4=总体均值 © X-N4σ2) 以X为横坐标,f)为纵坐标, 心 绘制的曲线就是正态曲线(normal curve) -00<X<十00 7
x f (x) µ -¥ < < + x ¥ 一 .正态分布的数学形式 ☺ f(X) = 随机变量 X 的频数 , 称为概率密度函数 (probability density function) ☺ s2 = 总体方差, µ = 总体均值 ☺ X~N(µ, s2) ☺ 以X为横坐标, f(X)为纵坐标, 绘制的曲线就是 正态曲线(normal curve) 7
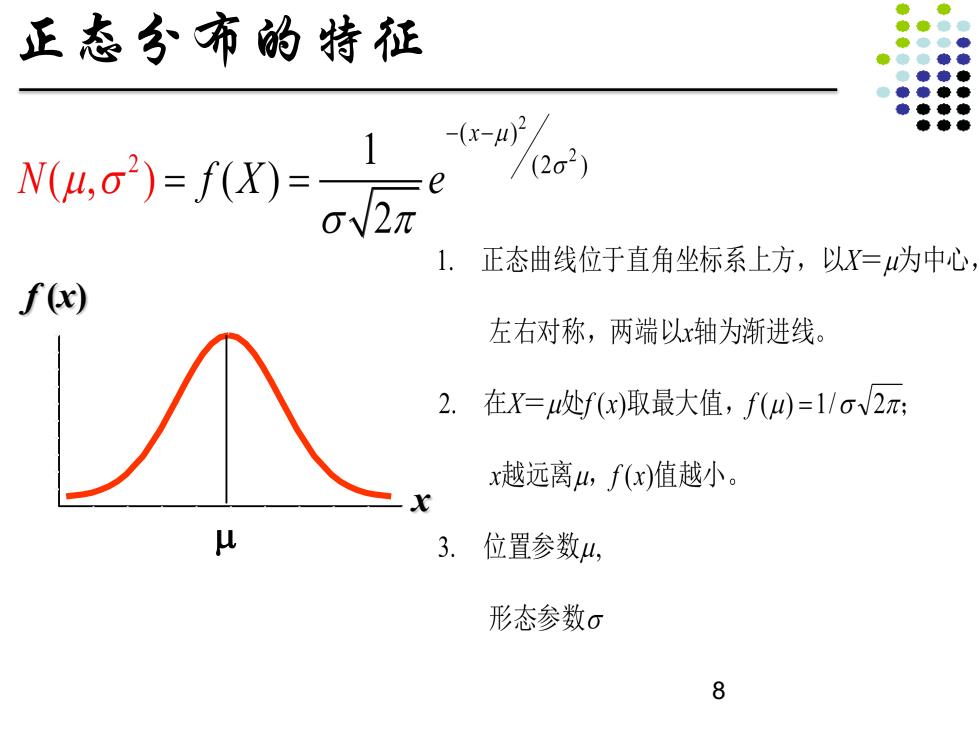
正态分布的特征 ● uoi=f=-人e" /22) 0√2元 1. 正态曲线位于直角坐标系上方,以X=为中心 f(x) 左右对称,两端以x轴为渐进线。 2.在X=处f(x)取最大值,f()=1/o2π: x越远离山,f(x)值越小。 3. 位置参数山, 形态参数o 8
正态分布的特征 x f (x) µ 8
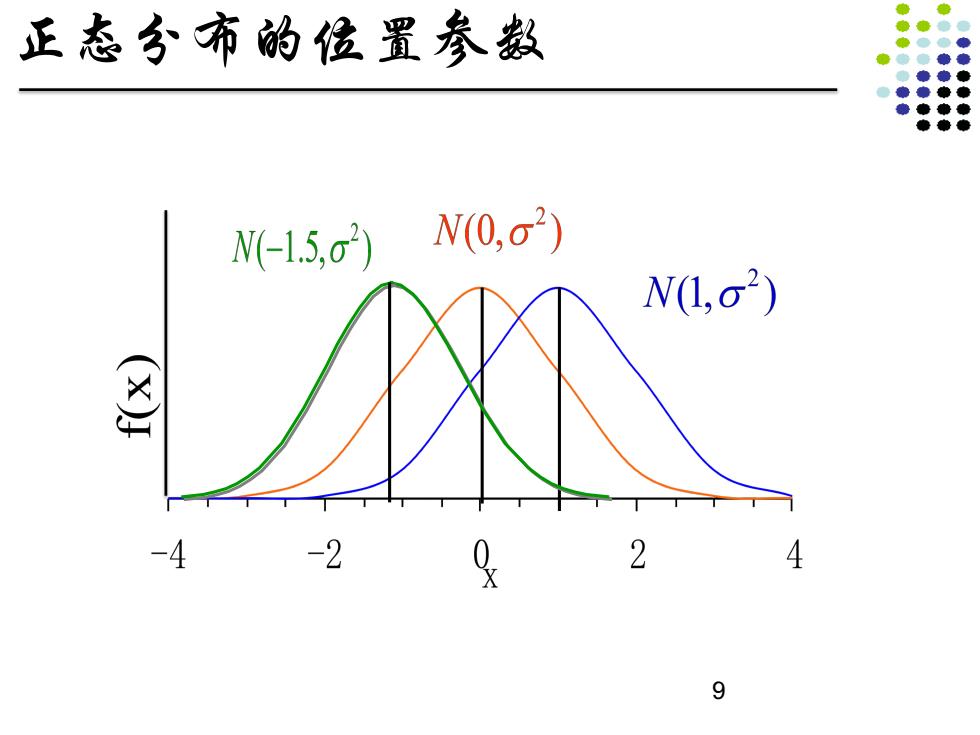
正态分布的位置参数 N-1.5G3) N(0,o2) N(I,o2) 多 -4 -2 2 4 9
Standard Curve Location Parameter (µ) 9 正态分布的位置参数