
2-1-1非负矩阵基本性质 引理设矩阵A,B,C,D∈Rnxn,向量x∈Rn. (1)若0≤A≤B,0≤C≤D,则0≤AC≤BD. (2)若0≤A≤B,则0≤A≤B*,k=1,2,. (3)若A>0且x≥0,则Ax>0. (4)若A≥0,x>0且Ax=0,则A=0. (留作课外自习) http://math.ecnu.edu.cn/-jypan 7/65
211 非负矩阵基本性质 引理 设矩阵 A, B, C, D ∈ R n×n , 向量 x ∈ R n . (1) 若 0 ≤ A ≤ B, 0 ≤ C ≤ D, 则 0 ≤ AC ≤ BD. (2) 若 0 ≤ A ≤ B, 则 0 ≤ Ak ≤ B k , k = 1, 2, . . .. (3) 若 A > 0 且 x ⪈ 0, 则 Ax > 0. (4) 若 A ≥ 0, x > 0 且 Ax = 0, 则 A = 0. (留作课外自习) http://math.ecnu.edu.cn/~jypan 7/65

基本性质 定理(基本性质)设A∈Cnxm,B∈Rnxn.如果A≤B,则p(A)≤p(A)≤p(B) (板书,利用性质:p(A)=im4/) 推论设A,B∈Rxn,若0≤A≤B,则p(A)≤p(B) 推论设A=[a∈Rmxn非负,Ak是A的k阶主子矩阵,其中1≤k≤n,则 p(A)≤p(A): 特别地,我们有 axaa≤p(A). 1≤达n http://math.ecmu.edu.cn/-jypan 8/65
基本性质 定理 (基本性质) 设 A ∈ C n×n , B ∈ R n×n . 如果 |A| ≤ B, 则 ρ(A) ≤ ρ(|A|) ≤ ρ(B). (板书, 利用性质: ρ(A) = lim k→∞ ∥Ak∥ 1/k F ) 推论 设 A, B ∈ R n×n , 若 0 ≤ A ≤ B, 则 ρ(A) ≤ ρ(B). 推论 设 A = [aij] ∈ R n×n 非负, Ak 是 A 的 k 阶主子矩阵, 其中 1 ≤ k ≤ n, 则 ρ(Ak) ≤ ρ(A). 特别地, 我们有 max 1≤i≤n aii ≤ ρ(A). http://math.ecnu.edu.cn/~jypan 8/65

非负矩阵的谱半径与矩阵行和及列和之间的关系 特殊情形 引理设A∈Rnxn非负. (1)如果A的行和是常数(即所有行和都相等),则p(A)=‖Al: (2)如果A的列和是常数(即所有列和都相等),则p(A)=‖Al1. (板书)】 http://math.ecmu.edu.cn/-jypan 9/65
非负矩阵的谱半径与矩阵行和及列和之间的关系 特殊情形 引理 设 A ∈ R n×n 非负. (1) 如果 A 的行和是常数 (即所有行和都相等), 则 ρ(A) = ∥A∥∞. (2) 如果 A 的列和是常数 (即所有列和都相等), 则 ρ(A) = ∥A∥1. (板书) http://math.ecnu.edu.cn/~jypan 9/65
非负矩阵的谱半径与矩阵行和及列和之间的关系(Cot.) 般情形 定理设A=[a∈Rnxn非负,则 min a≤p(A)≤ max 1这n1 1≤sn 且 min 1≤j於n a≤p(A)≤ max ≤n 1 (板书) http://math.ecmu.edu.cn/-jypan 10/65
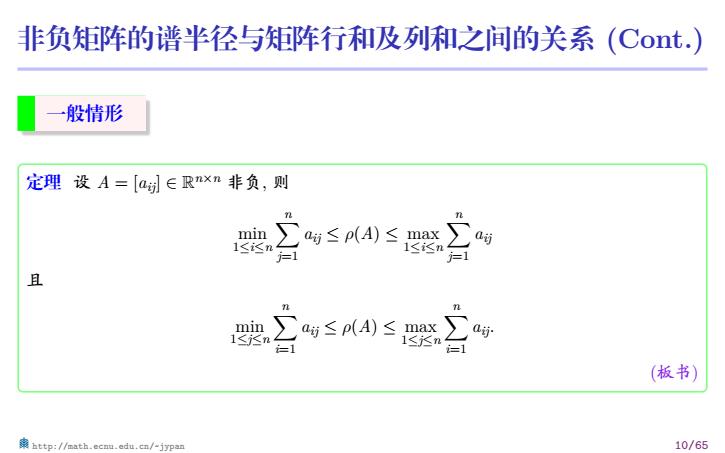
非负矩阵的谱半径与矩阵行和及列和之间的关系 (Cont.) 一般情形 定理 设 A = [aij] ∈ R n×n 非负, 则 min 1≤i≤n ∑n j=1 aij ≤ ρ(A) ≤ max 1≤i≤n ∑n j=1 aij 且 min 1≤j≤n ∑n i=1 aij ≤ ρ(A) ≤ max 1≤j≤n ∑n i=1 aij. (板书) http://math.ecnu.edu.cn/~jypan 10/65
两个推论 推论设A∈Rmxn非负.如果A的某一行或某一列的元素都是正的,则p(A)>0.特别 地,如果A>0则p(A)>0. 推论设A=[a∈Rxm非负.则对任意正向量x=[国,2,xT∈R”,都有 min l≤达nE a 和 1≤区n =1 -1 (考虑X-1AX即可,其中X=dig(,2,.,x)非奇异】 http://math.ecmu.edu.cn/-jypan 11/65
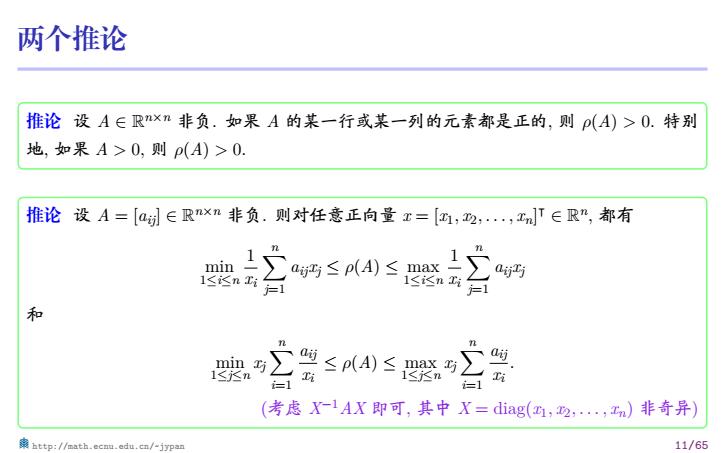
两个推论 推论 设 A ∈ R n×n 非负. 如果 A 的某一行或某一列的元素都是正的, 则 ρ(A) > 0. 特别 地, 如果 A > 0, 则 ρ(A) > 0. 推论 设 A = [aij] ∈ R n×n 非负. 则对任意正向量 x = [x1, x2, . . . , xn] ⊺ ∈ R n , 都有 min 1≤i≤n 1 xi ∑n j=1 aijxj ≤ ρ(A) ≤ max 1≤i≤n 1 xi ∑n j=1 aijxj 和 min 1≤j≤n xj ∑n i=1 aij xi ≤ ρ(A) ≤ max 1≤j≤n xj ∑n i=1 aij xi . (考虑 X−1AX 即可, 其中 X = diag(x1, x2, . . . , xn) 非奇异) http://math.ecnu.edu.cn/~jypan 11/65