中国地质大学：《机械设计》课程教学资源（PPT课件）第03章 机械零件的强度

当循环应力参数（om,g。)落在OAGC以内 时，表示不会发生疲劳破坏。 当应力点落在OA'GC以外 时，一定会发生疲劳破坏。 而正好落在A'GYC折线上 时，表示应力状况达到疲 劳破坏的极限值。 公式o1=o+W。om中的参数y为试件受循环弯曲应力 时的材料常数，其值由试验及下式决定 20-1- 60 00 对于碳钢，40.10.2，对于合金钢， y0.20.3

潘存云教授研制 σa σm σS 45˚ σ-1 G’ σ0 /2 C σ0 /2 45˚ D’ C G’ A’ O 而正好落在A’G’C折线上 时，表示应力状况达到疲 劳破坏的极限值。 0 2 1 0      − = − 对于碳钢，σ≈0.1~0.2，对于合金钢，σ≈0.2~0.3。 公式 中的参数σ为试件受循环弯曲应力 时的材料常数，其值由试验及下式决定  1  a   m =  +  − 当应力点落在OA’G’C以外 时，一定会发生疲劳破坏。 当循环应力参数（ σm，σa ）落在OA’G’C以内 时，表示不会发生疲劳破坏

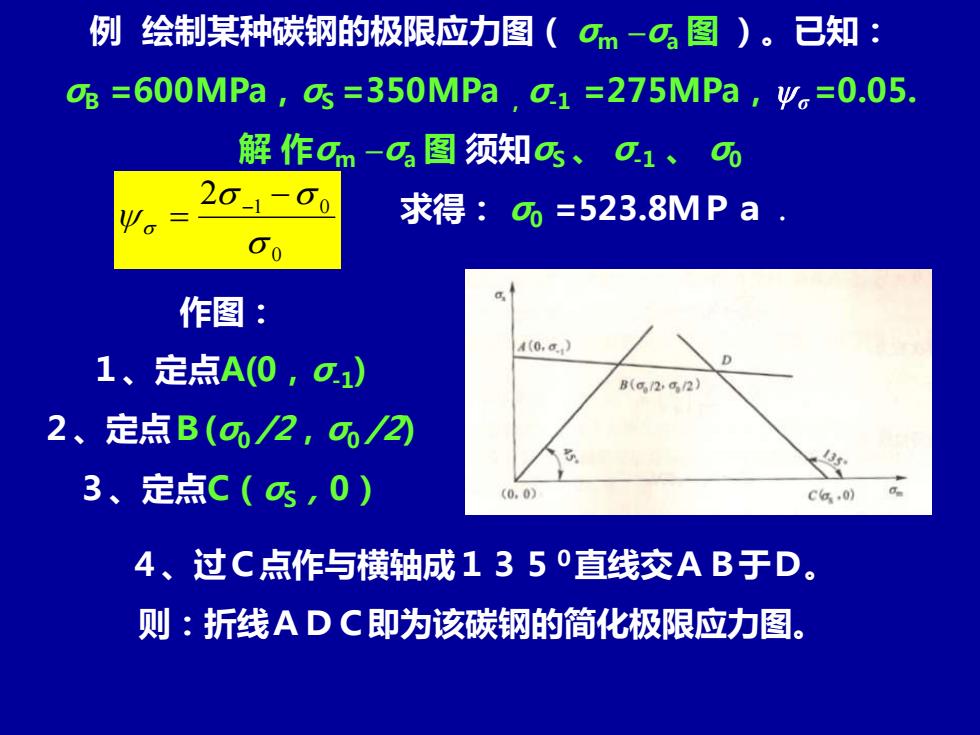
例绘制某种碳钢的极限应力图（σm-¤图）。已知： c%=600MPa,c=350MPa,g.1=275MPa,y。=0.05. 解作可m-可图须知s、g1、6 201-00 求得：©%=523.8MPa. 60 a. 作图： A(0,a,】 1、定点A(0,o1) B(g2,g2) 2、定点B(c/2,a02 3、定点C(匹，0) (0,0) Cg,0) 4、过C点作与横轴成1350直线交AB于D。 则：折线ADC即为该碳钢的简化极限应力图

例 绘制某种碳钢的极限应力图（ σm –σa 图 ）。已知： σB =600MPa，σS =350MPa ，σ-1 =275MPa，σ=0.05. 解 作σm –σa 图 须知σS 、 σ-1 、 σ0 由 求得： σ0 =523.8ＭＰａ． 0 2 1 0      − = − 作图： １、定点A(0，σ-1 ) ２、定点Ｂ(σ0 /2，σ0 /2) ３、定点C（σS，0） ４、过Ｃ点作与横轴成１３５０直线交ＡＢ于Ｄ。 则：折线ＡＤＣ即为该碳钢的简化极限应力图

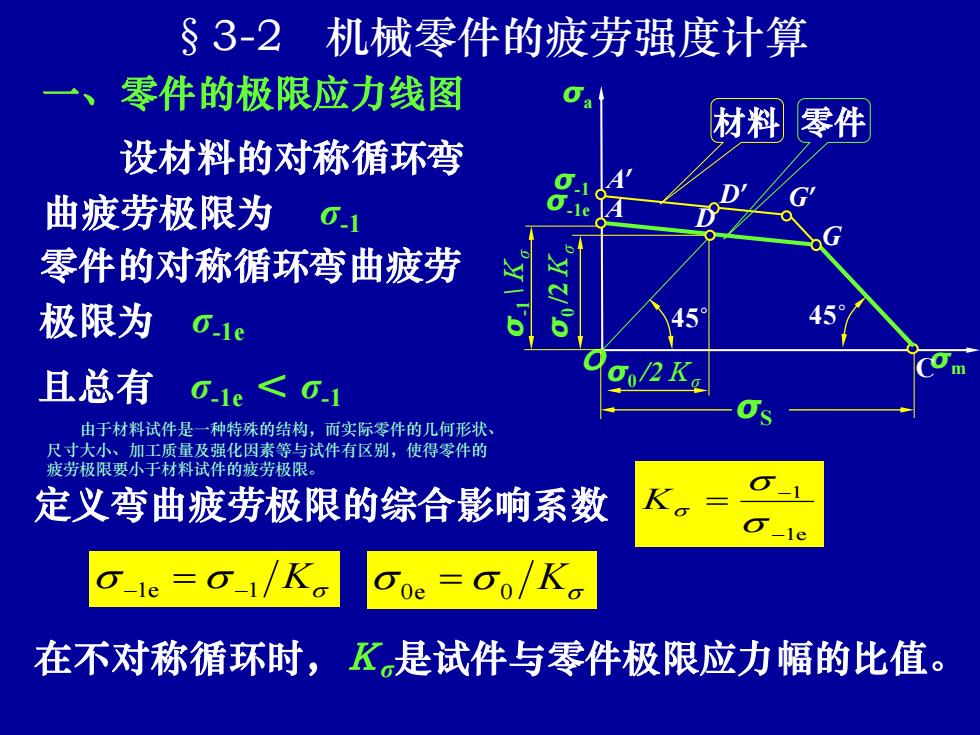
§3-2 机械零件的疲劳强度计算 、零件的极限应力线图 可a 厚件 设材料的对称循环弯 曲疲劳极限为ō1 零件的对称循环弯曲疲劳 极限为o.1e 且总有01e<01 80/2 由于材料试件是一种特殊的结构，而实际零件的几何形状 尺寸大小、加工质量及强化因素等与试件有区别，使得零件的 疲劳极限要小于材料试件的疲劳极限。 定义弯曲疲劳极限的综合影响系数 G-le =_1/Ko Goe=o/Ka 在不对称循环时，K是试件与零件极限应力幅的比值

σa Ｏ σm 潘存云教授研制 材料 σS σ-1 D’ A’ G’ C §3-2 机械零件的疲劳强度计算 一、零件的极限应力线图 由于材料试件是一种特殊的结构，而实际零件的几何形状、 尺寸大小、加工质量及强化因素等与试件有区别，使得零件的 疲劳极限要小于材料试件的疲劳极限。 定义弯曲疲劳极限的综合影响系数 1e 1 − − =   K 在不对称循环时，Ｋσ是试件与零件极限应力幅的比值。 σ-1 \Ｋσ σ0 /2Ｋσ σ0 /2 Ｋσ 零件的对称循环弯曲疲劳 极限为 σ-1e 设材料的对称循环弯 曲疲劳极限为 σ-1  −1e = −1 K  0e = 0 K 45˚ D A G 45˚ σ-1e 零件 且总有 σ-1e ＜ σ-1

直线AG的方程为 me =KoOpe+WaOme 或 直线CG的方程为 ae me ae 零件所受极限应力幅； me 零件所受极限平均应力； 零件受弯曲的材料特性； 弯曲疲劳极限的综合影响系数K。反映了应力集中、 尺寸因素、表面加工质量及强化等因素的综合影响结果。 其计算公式如下 其中：k。 有效应力集中系数；8。—尺寸系数； 表面质量系数； 强化系数

潘存云教授研制 σa Ｏ σm σS σ-1 D’ A’ G’ C σ-1 \Ｋσ A G 45˚ σ-1e 45˚ D ae me 1 1        = =  +  − − e e K  ae  me = s  +   1   ae   me =  +  或 − K 直线AＧ的方程为 直线CＧ的方程为 σ’ ae ——零件所受极限应力幅； σ’ me ——零件所受极限平均应力； σ e ——零件受弯曲的材料特性； 弯曲疲劳极限的综合影响系数Ｋσ 反映了应力集中、 尺寸因素、表面加工质量及强化等因素的综合影响结果。 其计算公式如下 其中：kσ ——有效应力集中系数； q k K       1 1 1       = + − βσ ——表面质量系数； εσ ——尺寸系数； βq ——强化系数。 C G

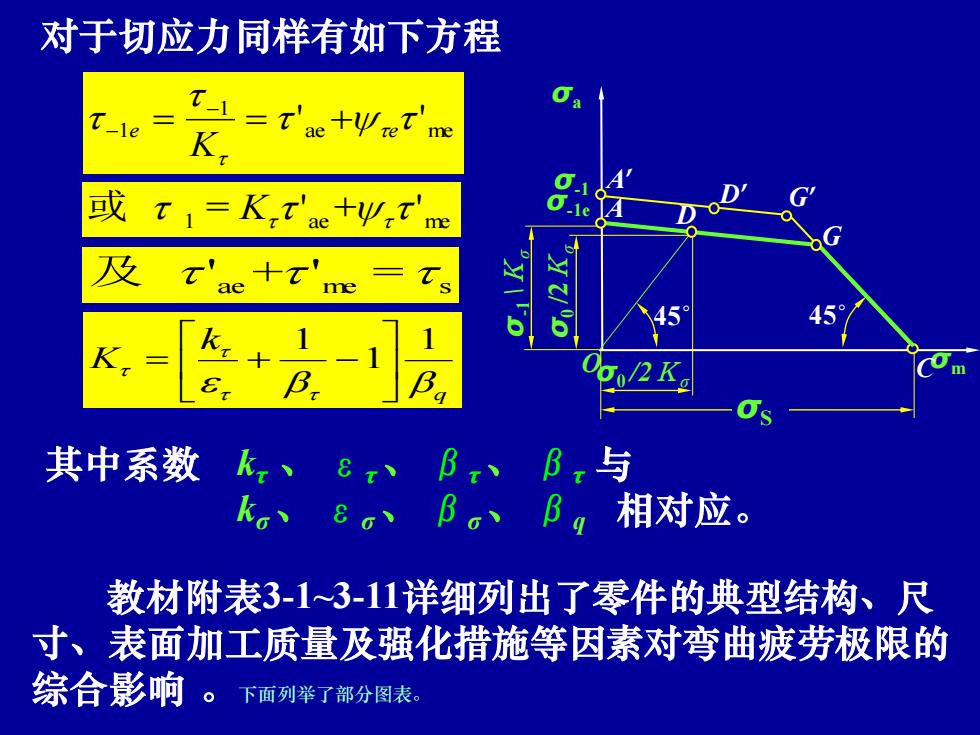
对于切应力同样有如下方程 _1e K 或t1=K,t'ae十yW,t'm 及 x'+' ae me -Ts K k+ 其中系数 、Bx、Bx与 ka、e、B。、Bg相对应。 教材附表3-13-11详细列出了零件的典型结构、尺 寸、表面加工质量及强化措施等因素对弯曲疲劳极限的 综合影响。下面列举了部分图表

潘存云教授研制 ae me 1 1  '   '     e e K = = + − − ae me = s 及  ' + '  1 ae me  =  ' +  ' 或 K  对于切应力同样有如下方程 其中系数 kτ 、 ετ、 βτ、 βτ 与 kσ 、 εσ 、 βσ 、 βq 相对应。 q k K      1 1 1       = + − 教材附表3-1~3-11详细列出了零件的典型结构、尺 寸、表面加工质量及强化措施等因素对弯曲疲劳极限的 综合影响 。下面列举了部分图表。 σa O σm σS σ-1 D’ A’ G’ C σ-1 \Ｋσ σ0 /2Ｋσ σ0 /2 Ｋσ 45˚ A D G 45˚ σ-1e