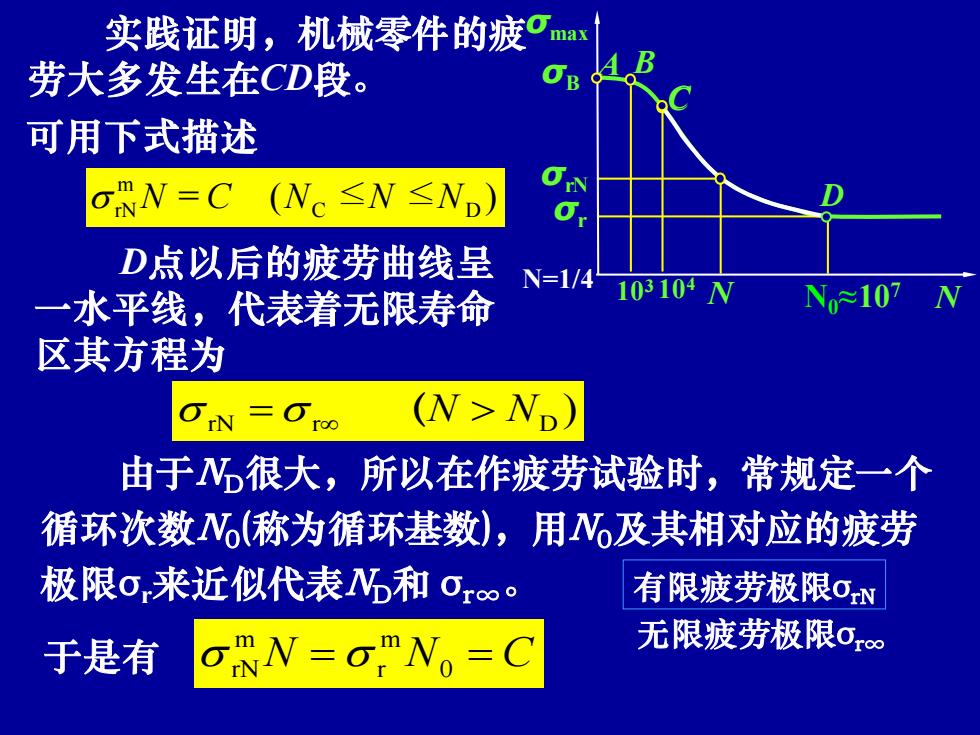
实践证明,机械零件的疲Cmax 劳大多发生在CD段。 可用下式描述 oRN=C(Nc≤N≤No) D点以后的疲劳曲线呈 N=1/4 一水平线,代表着无限寿命 103104N N≈107 区其方程为 (N>Np) 由于很大,所以在作疲劳试验时,常规定一个 循环次数W(称为循环基数),用Wo及其相对应的疲劳 极限o,来近似代表Nb和Or∞。 有限疲劳极限oN 于是有 7=O 无限疲劳极限·
潘存云教授研制 ) rN = r (N ND 由于ND很大,所以在作疲劳试验时,常规定一个 循环次数N0 (称为循环基数),用N0及其相对应的疲劳 极限σr来近似代表ND和 σr∞。 σmax N σr N0≈107 C D σrN N σB A N=1/4 D点以后的疲劳曲线呈 一水平线,代表着无限寿命 区其方程为 实践证明,机械零件的疲 劳大多发生在CD段。 = ( ≤ ≤ ) C D m rN N C N N N 可用下式描述 于是有 N = N0 = C m r m rN 104 C B 103 无限疲劳极限σr∞ 有限疲劳极限σrN
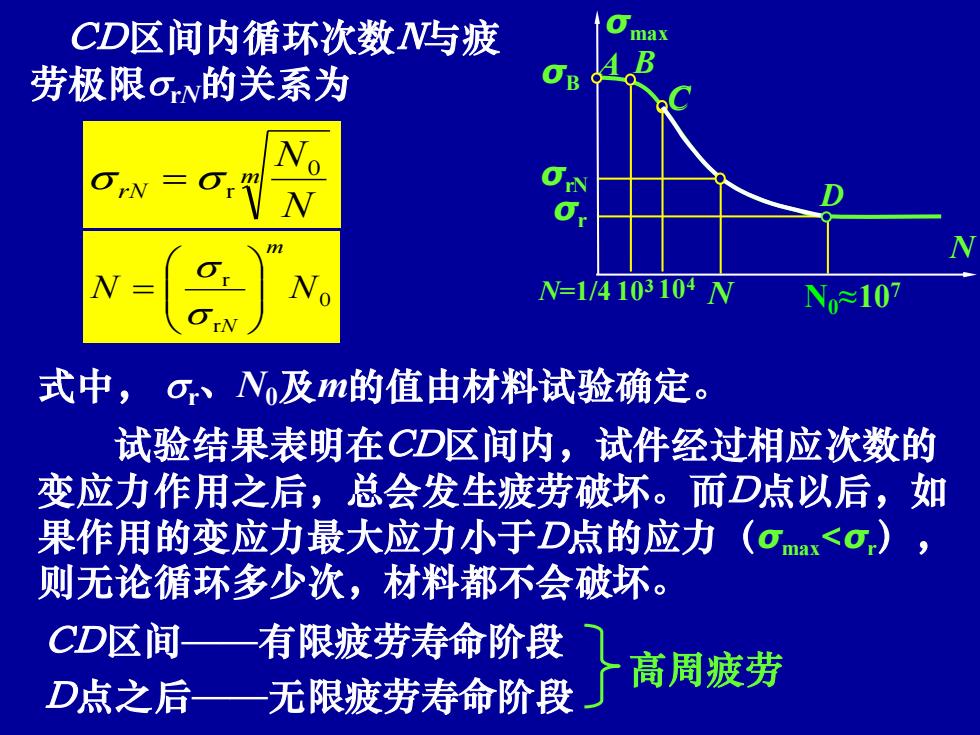
CD区间内循环次数N与疲 max 劳极限oN的关系为 N=1/4103104N N107 式中,o、N及m的值由材料试验确定。 试验结果表明在CD区间内,试件经过相应次数的 变应力作用之后,总会发生疲劳破坏。而D点以后,如 果作用的变应力最大应力小于D点的应力(口m<·,) 则无论循环多少次,材料都不会破坏。 CD区间—有限疲劳寿命阶段 无限疲劳寿命阶段 高周疲劳 D点之后
CD区间内循环次数N与疲 劳极限rN的关系为 式中, r、N0及m的值由材料试验确定。 m rN N N0 = r 0 r r N N m N = 试验结果表明在CD区间内,试件经过相应次数的 变应力作用之后,总会发生疲劳破坏。而D点以后,如 果作用的变应力最大应力小于D点的应力(σmax<σr), 则无论循环多少次,材料都不会破坏。 CD区间——有限疲劳寿命阶段 D点之后——无限疲劳寿命阶段 高周疲劳 潘存云教授研制 σmax N σr N0≈107 C σB A N=1/4 104 C B 103 D σrN N

例某材料的对称循环疲劳弯曲极限σ1=180MPa,取循环基数 N0=5*106,m=9,试求循环次数分别为7000、25000、62000 次时的有限弯曲疲劳极限。 解:由omN=o,mN0=C 得 "N 当循环次数N=7000时,0N=aNN =180× 5×106 7000 =373.57MPa "No 当循环次数N=25000时,0N=0N =180×N 5×10 25000 =324.30MPao "No 当循环次数N=620000时,0N=0√N =180× 5×10的 620000 =226.99MPa
例 某材料的对称循环疲劳弯曲极限σ-1=180MPa,取循环基数 N0=5*106 ,m=9,试求循环次数分别为7000、25000、62000 次时的有限弯曲疲劳极限。 解 :由 rN m• N= r m• N0=C 得
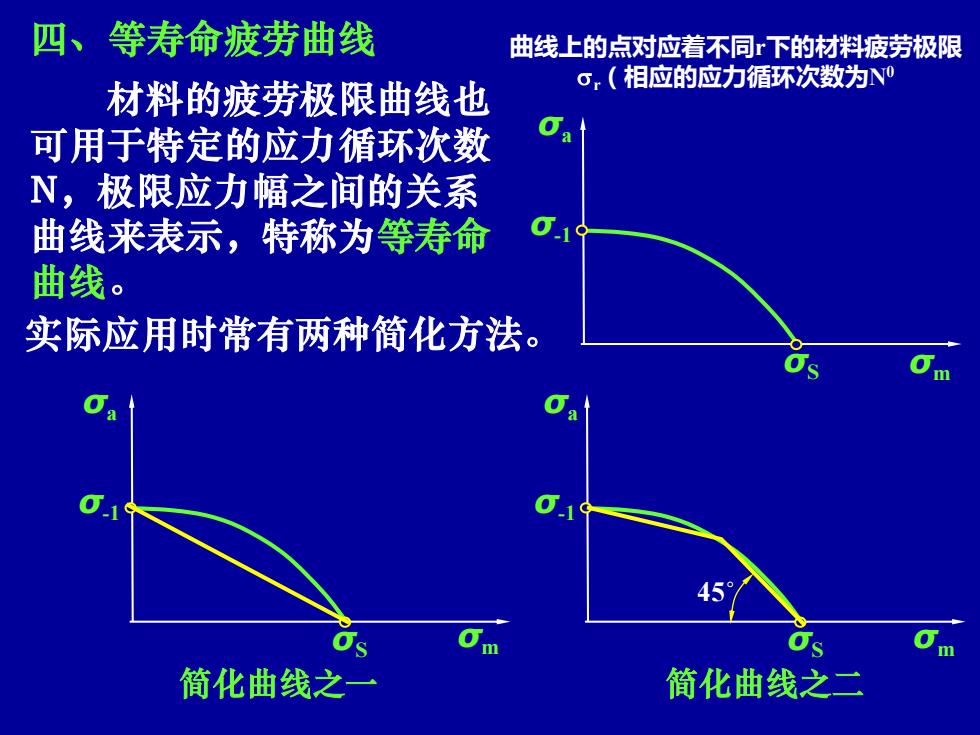
四、等寿命疲劳曲线 曲线上的点对应着不同下的材料疲劳极限 σ,(相应的应力循环次数为N0 材料的疲劳极限曲线也 可用于特定的应力循环次数 N,极限应力幅之间的关系 曲线来表示,特称为等寿命 曲线。 实际应用时常有两种简化方法。 简化曲线之一 简化曲线之二
σa σm 潘存云教授研制 σa σS σm σ-1 潘存云教授研制 σa σS σm σ-1 材料的疲劳极限曲线也 可用于特定的应力循环次数 N,极限应力幅之间的关系 曲线来表示,特称为等寿命 曲线。 简化曲线之一 简化曲线之二 四、等寿命疲劳曲线 实际应用时常有两种简化方法。 σS σ-1 45˚ 曲线上的点对应着不同r下的材料疲劳极限 r(相应的应力循环次数为N0
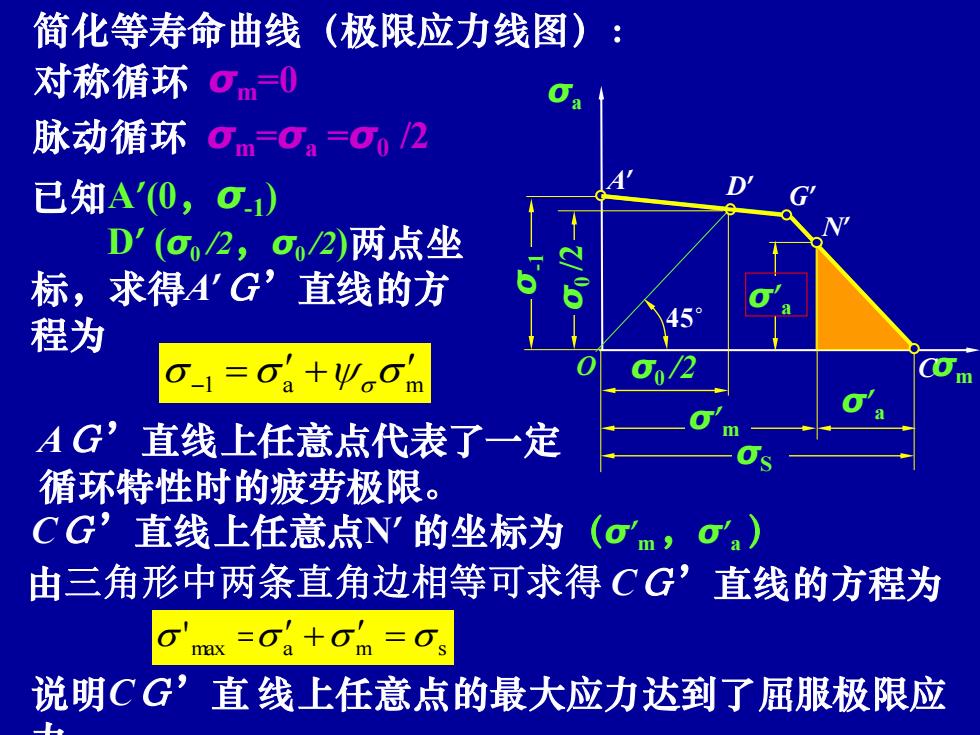
简化等寿命曲线 (极限应力线图) 对称循环0m=0 脉动循环gm=0。=02 已知A(0,g) D(g2,2)两点坐 标,求得A'G’直线的方 程为 C-=Og+VoOm m AG’直线上任意点代表了一定 循环特性时的疲劳极限。 CG’直线上任意点N'的坐标为(om,o.) 由三角形中两条直角边相等可求得CG’直线的方程为 G'mx =0a+Om =Os 说明CG’直线上任意点的最大应力达到了屈服极限应
σa σm σS 45˚ σ-1 O 潘存云教授研制 ' max = 简化等寿命曲线(极限应力线图): 已知A’(0,σ-1 ) D’ (σ0 /2,σ0 /2)两点坐 标,求得A’G’直线的方 程为 1 a m = + − a m = s + AG’直线上任意点代表了一定 循环特性时的疲劳极限。 对称循环 σm=0 A’ 脉动循环 σm =σa =σ0 /2 说明CG’直 线上任意点的最大应力达到了屈服极限应 力。 σ0 /2 σ0 /2 45˚ D’ σ’ m σ’ a CG’直线上任意点N’ 的坐标为(σ’ m ,σ’ a ) 由三角形中两条直角边相等可求得 CG’直线的方程为 σ’ a G’ C N’