
第3章 机械零件的强度 §3-1 材料的疲劳特性 §3-2 机械零件的疲劳强度计算 §3-3 机械零件的抗断裂强度 §3-4 机械零件的接触强度 HIGHER EDUCATION PRESS
第3章 机械零件的强度 §3-1 材料的疲劳特性 §3-2 机械零件的疲劳强度计算 §3-3 机械零件的抗断裂强度 §3-4 机械零件的接触强度

§3-1 材料的疲劳特性 一、应力的种类 静应力:0=常数 应力的大小和方向不随时间而变化或变化缓慢的应力。 零件相应的失效形式为塑性变形或断裂。 关于静应力状态下机械零件的强度计算, 《材料力学》已有详细介绍。 变应力:o随时间变化 零件相应的失效形式为疲劳破坏。 (大多数机械零、部件都是处于变应力状态下工作)
§3-1 材料的疲劳特性 一、应力的种类 静应力: σ=常数 应力的大小和方向不随时间而变化或变化缓慢的应力。 零件相应的失效形式为塑性变形或断裂。 关于静应力状态下机械零件的强度计算, 《材料力学》已有详细介绍。 变应力: σ随时间变化 零件相应的失效形式为疲劳破坏。 (大多数机械零、部件都是处于变应力状态下工作)
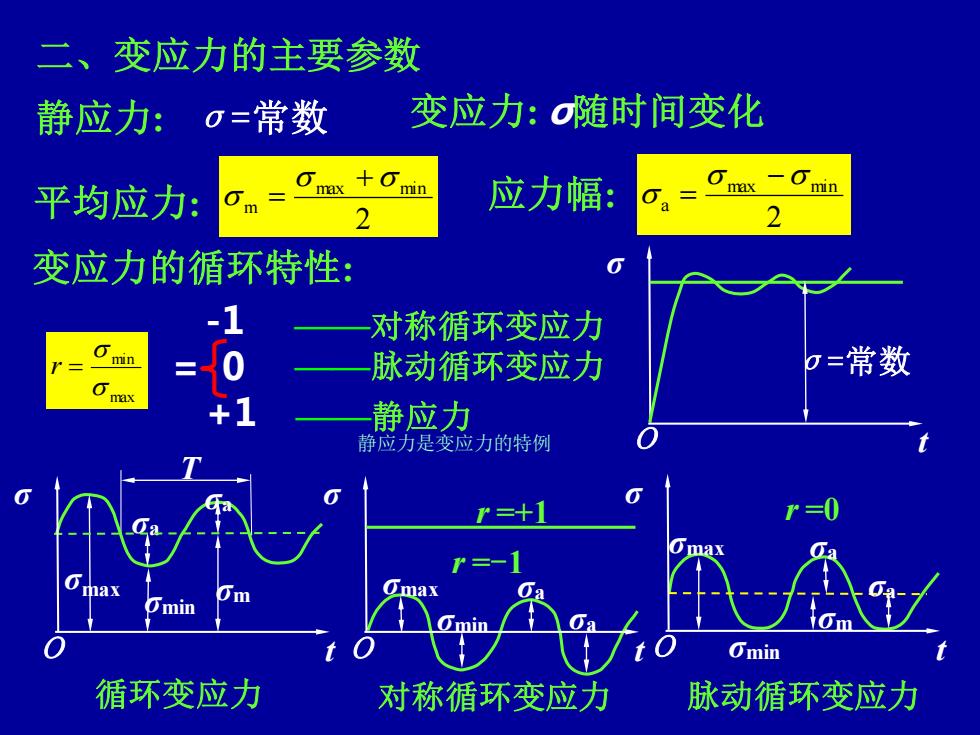
二、变应力的主要参数 静应力:o=常数 变应力:随时间变化 平均应力: 应力幅: Oma一Omin 2 变应力的循环特性: 对称循环变应力 脉动循环变应力 b=常数 静应力 静应力是变应力的特例 max min Omin 循环变应力 对称循环变应力 脉动循环变应力
潘存云教授研制 潘存云教授研制 潘存云教授研制 潘存云教授研制 二、变应力的主要参数 O t σ σ=常数 脉动循环变应力 r =0 静应力: σ=常数 变应力: σ随时间变化 2 max min m + 平均应力 = : 2 max min a − 应力幅: = 循环变应力 变应力的循环特性: max min r = 对称循环变应力 r =-1 ——脉动循环变应力 -1 ——对称循环变应力 = 0 +1 ——静应力 σmax σm T σmax σmin σa σa σm O t σ σmax σmin σa σa O t σ O t σ σa σa σmin r =+1 静应力是变应力的特例

变应力下,零件的损坏形式是疲劳断裂。 表面光滑 疲劳断裂过程: ▲零件表层产生微小裂纹 ▲随着循环次数增加,微裂 纹逐渐扩展 ▲当剩余材料不足以承受载 荷时,突然脆性断裂 表面粗糙 疲劳断裂是与应力循环次数(即使用寿命)有关的断裂。 疲劳断裂具有以下特征: ▲疲劳断裂的最大应力远比静应力下材料的强度极限 低,甚至比屈服极限低 不管脆性材料或塑性材料 疲劳断口均表现为无明显塑性变形的脆性突然断裂 ▲疲劳断裂是微观损伤积累到一定程度的结果 断裂面累积损伤处表面光滑,而折断区表面粗糙
潘存云教授研制 变应力下,零件的损坏形式是疲劳断裂。 ▲ 疲劳断裂的最大应力远比静应力下材料的强度极限 低,甚至比屈服极限低 ▲ 疲劳断口均表现为无明显塑性变形的脆性突然断裂 ▲ 疲劳断裂是微观损伤积累到一定程度的结果 不管脆性材料或塑性材料, ▲零件表层产生微小裂纹 疲劳断裂过程: ▲随着循环次数增加,微裂 纹逐渐扩展 ▲当剩余材料不足以承受载 荷时,突然脆性断裂 疲劳断裂是与应力循环次数(即使用寿命)有关的断裂。 疲劳断裂具有以下特征: ▲ 断裂面累积损伤处表面光滑,而折断区表面粗糙 表面光滑 表面粗糙
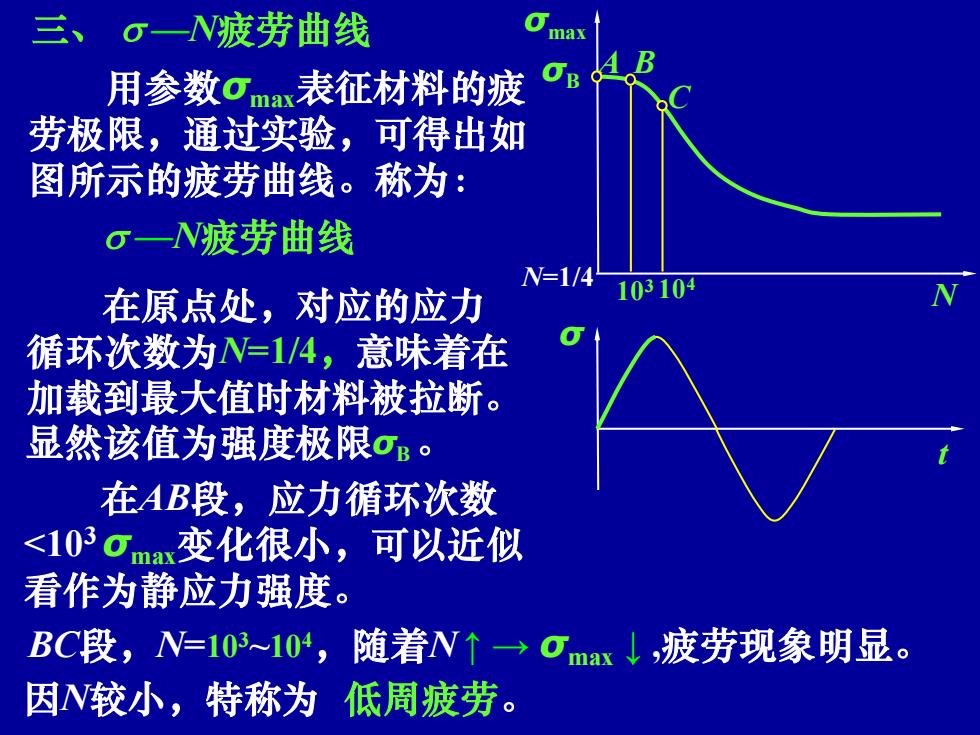
三、 σ一N疲劳曲线 max 用参数gma表征材料的疲 劳极限,通过实验,可得出如 图所示的疲劳曲线。称为: o一N疲劳曲线 N=1/4 在原点处,对应的应力 103104 循环次数为N=1/4,意味着在 加载到最大值时材料被拉断。 显然该值为强度极限σ。 在AB段,应力循环次数 <I03om变化很小,可以近似 看作为静应力强度。 BC段,N=10~10,随着N↑→Oms↓,疲劳现象明显。 因N较小,特称为低周疲劳
潘存云教授研制 潘存云教授研制 σmax N 三、 —N疲劳曲线 用参数σmax表征材料的疲 劳极限,通过实验,可得出如 图所示的疲劳曲线。称为: —N疲劳曲线 104 C 在原点处,对应的应力 循环次数为N=1/4,意味着在 加载到最大值时材料被拉断。 显然该值为强度极限σB 。 B 103 σ t σB A N=1/4 在AB段,应力循环次数 <103 σmax变化很小,可以近似 看作为静应力强度。 BC段,N=103~104,随着N ↑ → σmax ↓ ,疲劳现象明显。 因N较小,特称为 低周疲劳