
4,1电容元件 6、主要结论 (1)电容的伏安关系是微积分关系,因此电容元件是动态元件。而电阻 元件的伏安关系是代数关系,电阻是一个即时(瞬时)元件。 (2)由电容VAR的微分形式可知:①任意时刻,通过电容的电流与该时 安电子科技大学电路与系统 刻电压的变化率成正比。当电容电流i为有限值时,其d/dt也为有限 值,则电压山必定是连续函数,此时电容电压是不会跃变的。②当电容 电压为直流电压时,则电流=0,此时电容相当于开路,故电容有隔 直流的作用。 (3)由电容VAR的积分形式可知:在任意时刻t,电容电压u是此时刻以 前的电流作用的结果,它“记载”了以前电流的“全部历史”。即电 多媒体室制 容电压具有“记忆”电流的作用,故电容是一个记忆元件,而电阻是 无记忆元件。 (4)电容是一个储能元件,它从外部电路吸收的能量,以电场能量的形 式储存于自身的电场中。电容C在某一时刻的储能只与该时刻电容电 压有关。 41 回目
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 6、主要结论 第 4-11 页 前一页 下一页 返回本章目录 (1)电容的伏安关系是微积分关系,因此电容元件是动态元件。而电阻 元件的伏安关系是代数关系,电阻是一个即时(瞬时)元件。 (2)由电容VAR的微分形式可知:①任意时刻,通过电容的电流与该时 刻电压的变化率成正比。当电容电流i为有限值时,其du/dt也为有限 值,则电压u必定是连续函数,此时电容电压是不会跃变的。②当电容 电压为直流电压时,则电流i = 0,此时电容相当于开路,故电容有隔 直流的作用。 (3)由电容VAR的积分形式可知:在任意时刻t,电容电压u是此时刻以 前的电流作用的结果,它“记载”了以前电流的“全部历史”。即电 容电压具有“记忆”电流的作用,故电容是一个记忆元件,而电阻是 无记忆元件。 (4)电容是一个储能元件,它从外部电路吸收的能量,以电场能量的形 式储存于自身的电场中。电容C在某一时刻的储能只与该时刻t电容电 压有关
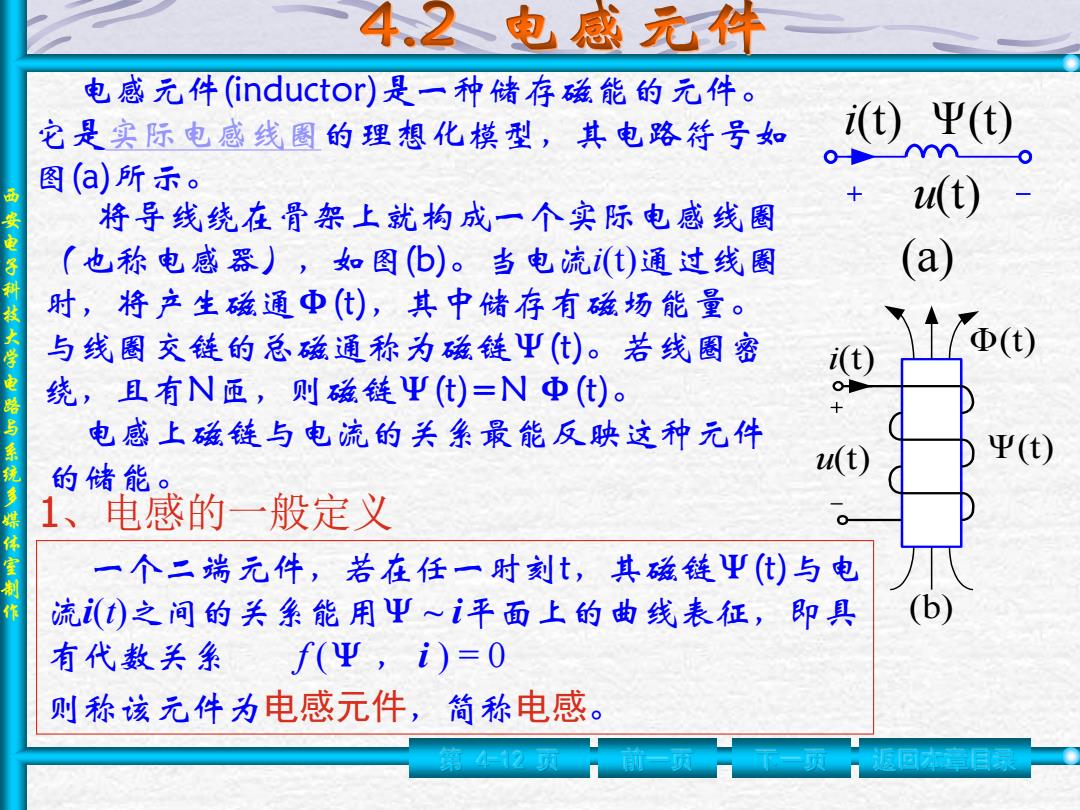
、电感元件 电感元件(inductor)是一种储存磁能的元件。 它是实际电感线圈的理想化模型,其电路待号如 (t)Ψ() 图(a)所示。 西 安电 将导线绕在骨架上就构成一个实际电感线圈 2u(t) (也称电感器),如图(b)。当电流()通过线圈 (a) 时,将产生磁通Φ(),其中储存有磁场能量。 大学 与线圈交链的总磁通称为磁链Ψ()。若线圈密 电 绕,且有N匝,则磁链Ψ(t)=NΦ(t)。 电感上磁链与电流的关系最能反映这种元件 系统 的储能。 u(t) 平(t) 多 1、电感的一般定义 体 室制 一个二端元件,若在任一时刻t,其磁链Ψ()与电 流()之间的关系能用Ψ~平面上的曲线表征,即具 有代数关象 f(Ψ,i)=0 则称该元件为电感元件,简称电感
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-12 页 前一页 下一页 返回本章目录 电感元件(inductor)是一种储存磁能的元件。 它是实际电感线圈的理想化模型,其电路符号如 图(a)所示。 (a) i(t) Ψ(t) u(t) 将导线绕在骨架上就构成一个实际电感线圈 (也称电感器),如图(b)。当电流i(t)通过线圈 时,将产生磁通Φ(t),其中储存有磁场能量。 与线圈交链的总磁通称为磁链Ψ(t)。若线圈密 绕,且有N匝,则磁链Ψ(t)=N Φ(t)。 i(t) u(t) Φ(t) Ψ(t) (b) 电感上磁链与电流的关系最能反映这种元件 的储能。 1、电感的一般定义 一个二端元件,若在任一时刻t,其磁链Ψ(t)与电 流i(t)之间的关系能用Ψ ~ i平面上的曲线表征,即具 有代数关系 f (Ψ , i ) = 0 则称该元件为电感元件,简称电感

4.2电感元件 电感也分:时变和时不变的,线性的和非线性的。 线性时不变电感的外特性(韦安特性)是Ψ平面上一条过原点的直线, 且其斜率L不随时间变化,如图()所示。其表达式可写为: 西 安电子科 Y(t)=Li(t) 其中L就是电感元件的值,单位为:亨[利](H)。磁链的单 大学电 位:韦[伯](Wb)。对于线性时不变电感,L为正实常数。 2、电感的VAR(或VCR) a) 路与 电感中,当电流变化时,磁链也发生变化,从而产生感应电压。在电流 系统 与电压参考方向关联时,若电压参考方向与磁通的方向待合右手法则,根据 多 法拉第电磁感应定律,感应电压()与磁链的变化率成正比,即: (t)= dΨ(t) 体 对线性电感,由于)=L(),故有 制 u(t)= (t) Ψ) 2(t) 称电感VAR的微分形式 6) 43
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 4-13 页 前一页 下一页 返回本章目录 (a) Ψ 0 i L 线性时不变电感的外特性(韦安特性)是Ψ~i平面上一条过原点的直线, 且其斜率L不随时间变化,如图(a)所示。其表达式可写为: Ψ(t) = L i(t) 其中L就是电感元件的值,单位为:亨[利](H)。磁链的单 位:韦[伯](Wb)。对于线性时不变电感,L为正实常数。 2、电感的VAR(或VCR) 电感中,当电流变化时,磁链也发生变化,从而产生感应电压。在电流 与电压参考方向关联时,若电压参考方向与磁通的方向符合右手法则,根据 法拉第电磁感应定律,感应电压u(t)与磁链的变化率成正比,即: t t u t d d ( ) ( ) = (b) i(t) Ψ(t) u(t) L 对线性电感,由于Ψ(t) = L i(t),故有 t i u t L d d ( ) = 称电感VAR的微分形式 电感也分:时变和时不变的,线性的和非线性的