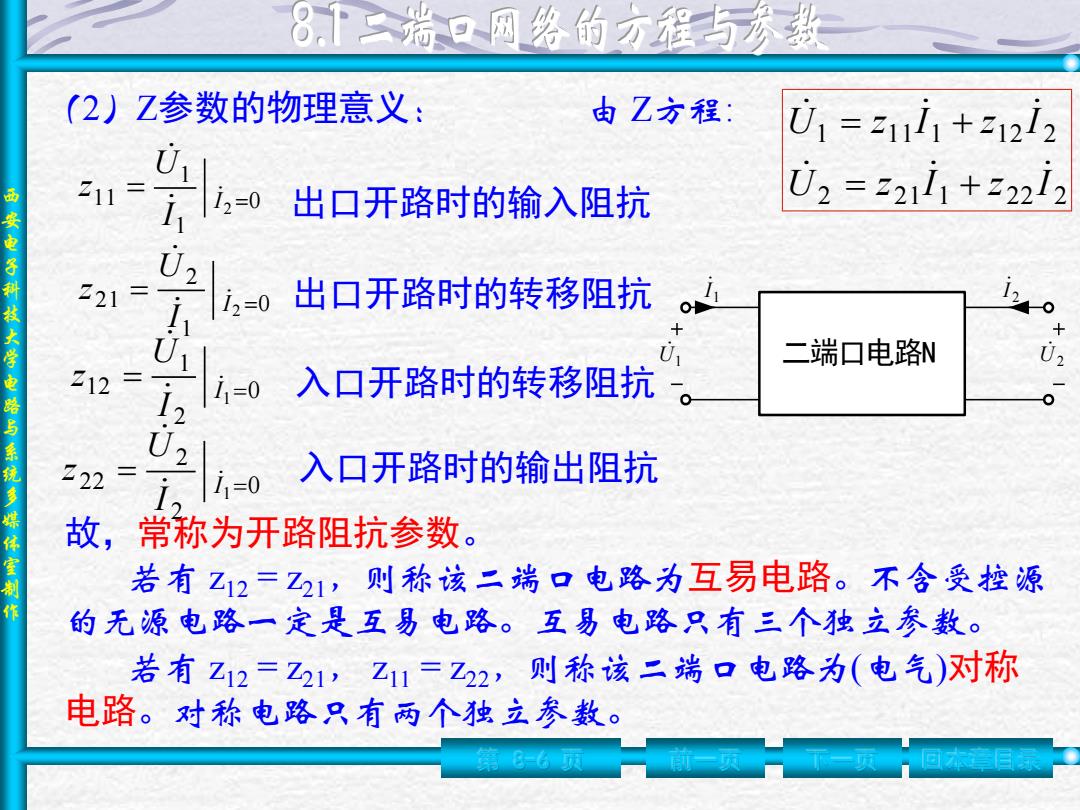
8「二瑞口网您的方程与秀数 (2)Z参数的物理意义: 由Z方程: 01=211i1+21212 U 西 211= i2=0 出口开路时的输入阻抗 02=321i1+z22i2 安电子科技大学电路与系统多媒体室制 02 221= i2=0 出口开路时的转移阻抗 U 二端口电路N 212 1-0 入口开路时的转移阻抗 U2 Z22 i=0 入口开路时的输出阻抗 故, 常称为开路阻抗参数。 若有乙12=Z21,则称该二端口电路为互易电路。不含受控源 的无源电路一定是互易电路。互易电路只有三个独立参数。 若有Z12=Z21,Z11=Z22,则称该二端口电路为(电气)对称 电路。对称电路只有两个独立参数
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-6 页 前一页 下一页 回本章目录 由 Z方程: 0 1 1 11 2 = = I I U z 出口开路时的输入阻抗 0 1 2 21 2 = = I I U z 出口开路时的转移阻抗 0 2 1 12 1 = = I I U z 入口开路时的转移阻抗 0 2 2 22 1 = = I I U z 入口开路时的输出阻抗 故,常称为开路阻抗参数。 (2)Z参数的物理意义: 2 21 1 22 2 1 11 1 12 2 U z I z I U z I z I = + = + 若有 z12 = z21,则称该二端口电路为互易电路。不含受控源 的无源电路一定是互易电路。互易电路只有三个独立参数。 若有 z12 = z21, z11 = z22,则称该二端口电路为(电气)对称 电路。对称电路只有两个独立参数。 U1 二端口电路N U2 1 I 2 I
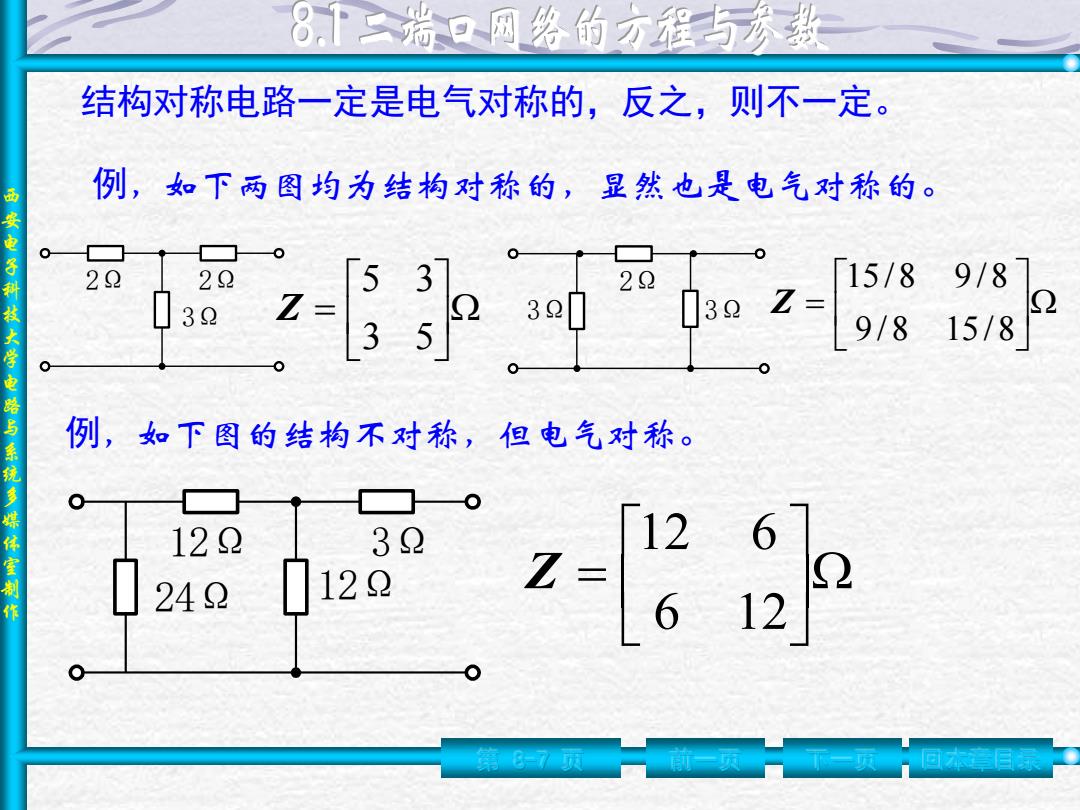
8「二瑞口网络的方程与参数 结构对称电路一定是电气对称的,反之,则不一定。 例,如下两图均为结构对称的,显然也是电气对称的。 一安电子科技大学电路与系统多媒体室制作 22 22 9/8 0 15/8 30 例,如下图的结构不对称,但电气对称。 ☐0 122 32 12 6 249 0129 Z= 6 12 87页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-7 页 前一页 下一页 回本章目录 结构对称电路一定是电气对称的,反之,则不一定。 例,如下两图均为结构对称的,显然也是电气对称的。 2Ω 2Ω 3Ω 2Ω 3Ω 3Ω = 3 5 5 3 Z = 9 /8 15/8 15/8 9 /8 Z 例,如下图的结构不对称,但电气对称。 12Ω 24Ω 12Ω 3Ω = 6 12 12 6 Z
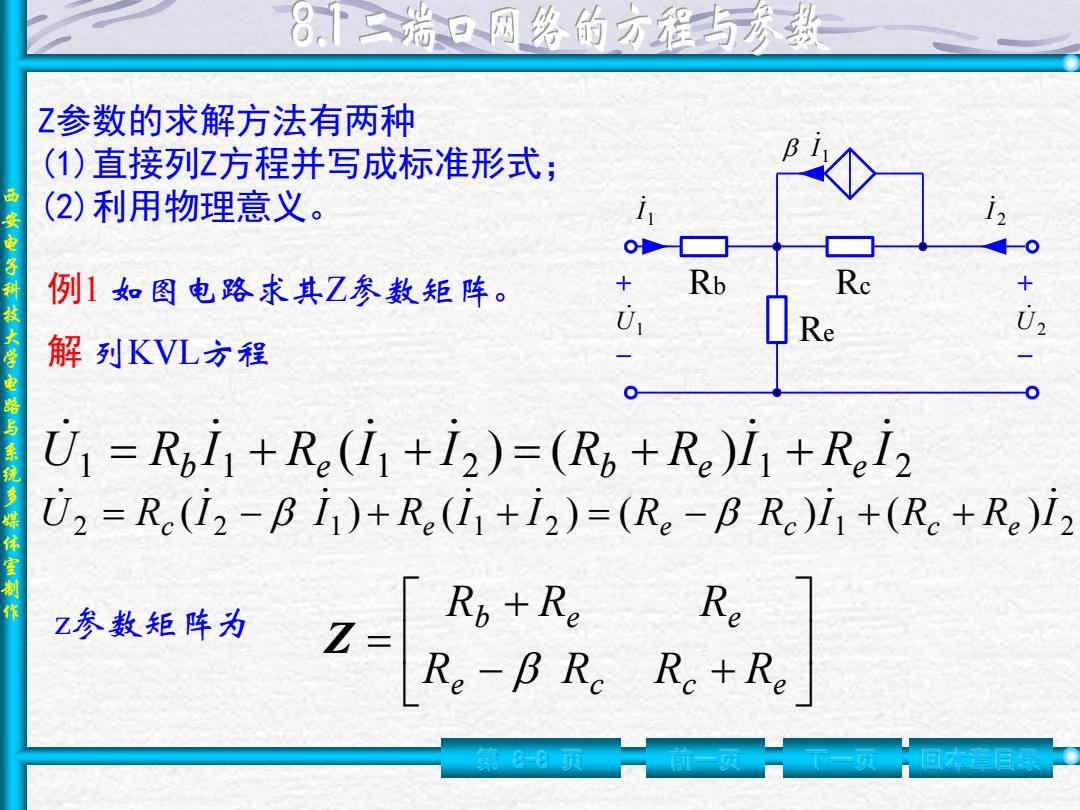
8下二瑞口网络的方程与秀数 Z参数的求解方法有两种 (1)直接列z方程并写成标准形式; (2)利用物理意义。 西安电子科技大学电路与系统多媒体室制作 例1如图电路求其Z参数矩阵。 Rb Re 01 Re 解列KVL方程 U=Rpi+Re(i+i2)=(Rp+Re)i+Rei2 U2=R(I2-BI1)+Re(I1+12)=(R。-BRc)I1+(R。+Re)I2 Z参数矩阵为 Ro+Re Re Z= Re-BR。Rc+Re 86页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-8 页 前一页 下一页 回本章目录 例1 如图电路求其Z参数矩阵。 U1 U2 1 I 2 I 1 I Rb Re Rc 解 列KVL方程 1 1 1 2 1 2 U R I R (I I ) (R R )I R I b e b e e = + + = + + 2 2 1 1 2 1 2 U R (I I ) R (I I ) (R R )I (R R )I c e e c c e = − + + = − + + z参数矩阵为 − + + = e c c e b e e R R R R R R R Z Z参数的求解方法有两种 (1)直接列Z方程并写成标准形式; (2)利用物理意义
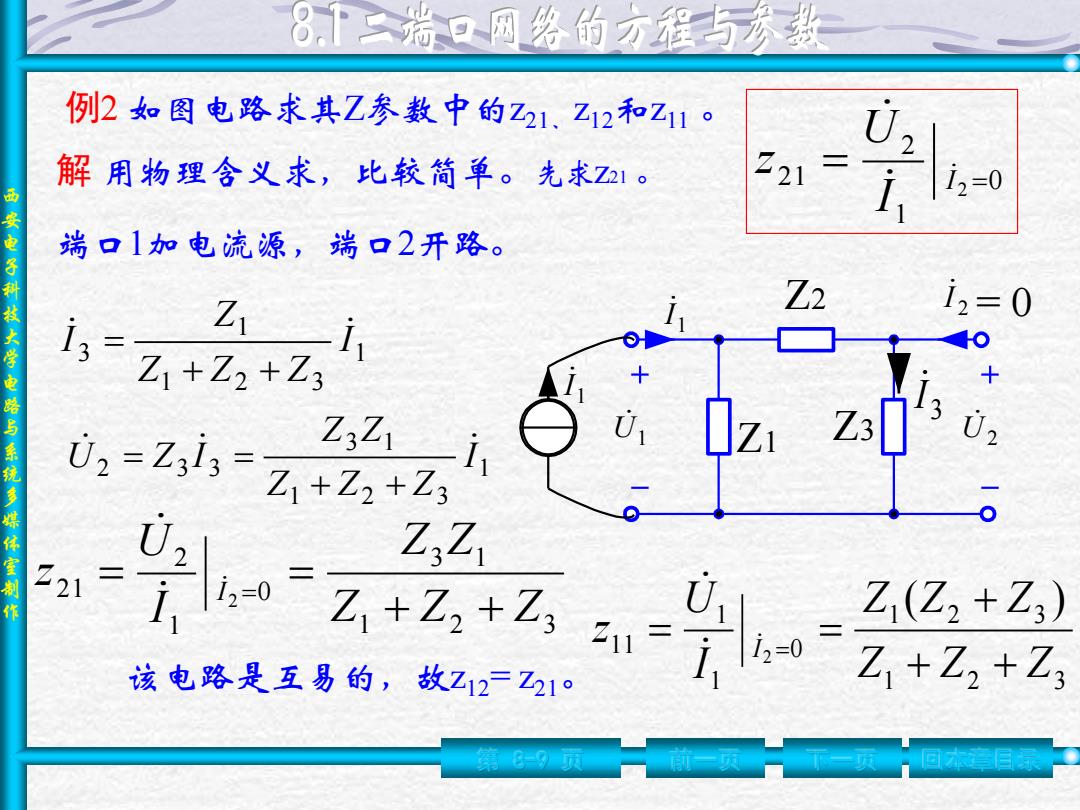
8「一瑞口网络的方程与秀数 例2如图电路求其Z参数中的Z21.Z12和Z11。 解用物理含义求,比较简单。先求Z21。 21 -0 端口1如电流源,端口2开路。 西安电子科技大学电路与系统多媒体室制 一i Z Z2 12=0 13 Z1+Z2+Z3 U2=Z3l3= Z3Z +2+石 I Z21 02 Z(Z2+Z3) 该电路是互易的,故Z12Z210 Z +Z,Z3 8-9页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-9 页 前一页 下一页 回本章目录 U1 U2 1 I 2 I Z1 Z2 Z3 1 I = 0 解 用物理含义求,比较简单。先求z21 。 端口1加电流源,端口2开路。 1 1 2 3 1 3 I Z Z Z Z I + + = 3 I 1 1 2 3 3 1 2 3 3 I Z Z Z Z Z U Z I + + = = 1 2 3 3 1 0 1 2 2 1 2 Z Z Z Z Z I U z I + + = = = 该电路是互易的,故z12= z21。 例2 如图电路求其Z参数中的z21、z12和z11 。 0 1 2 21 2 = = I I U z 1 2 3 1 2 3 0 1 1 1 1 ( ) 2 Z Z Z Z Z Z I U z I + + + = = =
8下二瑞口网络的方程与参数 例3如图电路, 己知Us=15V,Rs=22,N的z参数矩阵 73 Z= 2,若R=22,求U2及二端口电路吸收的功率。 34 解 列二端口电路的Z方程,得 Rs U1=7L1+3L2(1) 一安电子科技大学电路与系统多媒体室制作 U2=3L1+4L2(2) 列出输入口KVL方程,有 U U2 Us=2I1+U1(3) 对R,由欧姆定律得 U2=-212 (4) (1)代入(3)及(2)代入(4)并整理得 9L1+3L2=Us=15 3L1+6L2=0 解得I1=2A,I2=-1A代入(1)(4)得U1=11V,U2=2V PN=U1I1+U2I2=11×2+2×(-1)=20W
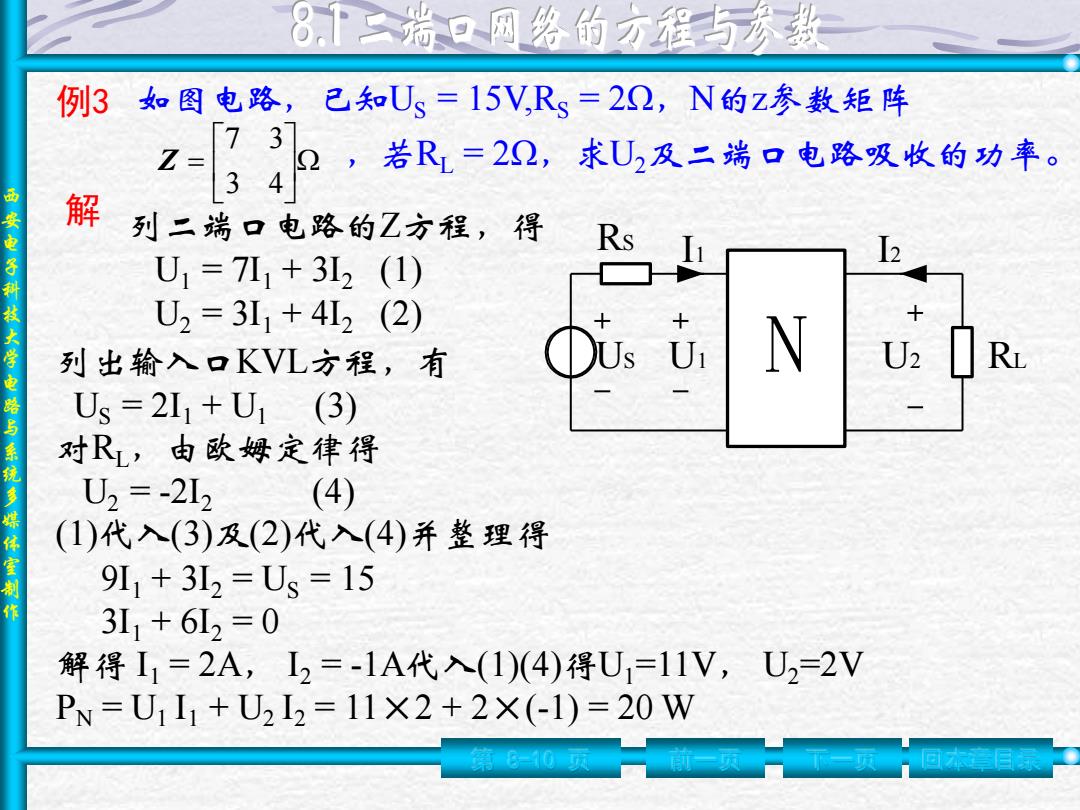
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-10 页 前一页 下一页 回本章目录 例3 如图电路,已知US = 15V,RS = 2Ω,N的z参数矩阵 = 3 4 7 3 Z ,若RL = 2Ω,求U2及二端口电路吸收的功率。 解 列二端口电路的Z方程,得 U1 = 7I1 + 3I2 (1) U2 = 3I1 + 4I2 (2) 列出输入口KVL方程,有 US = 2I1 + U1 (3) 对RL,由欧姆定律得 U2 = -2I2 (4) (1)代入(3)及(2)代入(4)并整理得 9I1 + 3I2 = US = 15 3I1 + 6I2 = 0 解得 I1 = 2A, I2 = -1A代入(1)(4)得U1=11V, U2=2V PN = U1 I1 + U2 I2 = 11×2 + 2×(-1) = 20 W US N RS U1 U2 I1 I2 RL