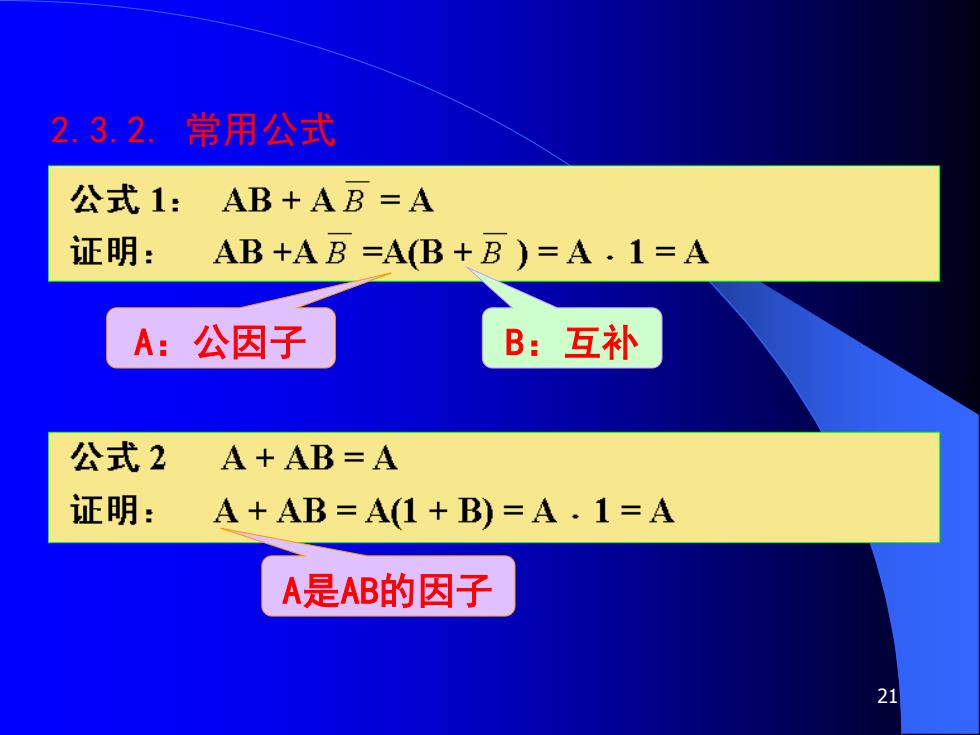
2.3.2.常用公式 公式1:AB+AB=A 证明: AB+AB=A(B+B)=A·1=A A:公因子 B:互补 公式2 A+AB=A 证明: A+AB=A(1+B)=A·1=A A是AB的因子 21
21 2.3.2. 常用公式 A:公因子 B:互补 A是AB的因子

公式3 A+4B=A+B 证明: A+4B=(A+4)(A+B)=1(A+B)=A+B A的反函数 是因子 与互补变量A相与的 添加项 B、C是第三项 公式4 AB+4C+BC=AB+4C 证明: AB+4C+BC=AB+4C+BC(A+4) =AB+4C+ABC+4 BC =AB(1+C)+AC(1+B) =AB+4C 推论: AB+4C+BCDE=AB+4C
22 A的反函数 是因子 与互补变量A相与的 添加项 B、C是第三项

常用公式 常用公式 证明 ① AB+AB=A AB+AB=A(B+B)=A·1=A ② A+AB=A A+AB=A(1+B)=A·1=A ③A+AB=A+B A+AB=(A+A)(A+B) =1·(A+B)=A+B ④AB+AC+BC=AB+AC 原式=AB+AC+BC(A+A) 推论: =AB+AC+ABC+ABC AB+4C+BCDE=AB+4C =AB(1+C)+AC(1+B) =AB+AC 需记忆 23
23 常用公式 需记忆

2.4.1代入定理 在任何一个包含A的逻辑式中,若以另外一个逻 辑式代入式中所有A的位置,则等式仍然成立。这就 是所谓的代入定理。 理论依据:任何一个逻辑函数也和任何一个逻辑 变量一样,只有逻辑0和逻辑1两种取值。因此,可将 逻辑函数作为一个逻辑变量对待 ABC =A+B+C 推广 ABC·=A+B+C+. 利用代入规则可以扩大公式的应用范围。 24
24 在任何一个包含A的逻辑式中,若以另外一个逻 辑式代入式中所有A的位置,则等式仍然成立。这就 是所谓的代入定理。 2. 4. 1 代入定理 推广 利用代入规则可以扩大公式的应用范围。 理论依据:任何一个逻辑函数也和任何一个逻辑 变量一样,只有逻辑0和逻辑1两种取值。因此,可将 逻辑函数作为一个逻辑变量对待

2.4.2反演定理 对任何一个逻辑表达式Y作反演变换,可得Y的 反函数V。这个规则叫做反演定理。 反演变换: Y=4+B+CD+0 46 7=AB.(C+D)1 c02→61 Y=A+B+C+D+E 原变量→反变量 Y=AB.C.D.E 反变量→原变量 7=A·(B+C+D+E) 运用反演定理时,要注意运算的优先顺序(先 括号、再相与,最后或) ,必要时可加或减扩号
25 2.4.2 反演定理 运用反演定理时,要注意运算的优先顺序(先 括号、再相与,最后或) ,必要时可加或减扩号。 ( ) 1 0 = + = + + + Y A B C D Y A B CD Y A (B C D E) Y A B C D E Y A B C D E = + + + = = + + + + 对任何一个逻辑表达式Y 作反演变换,可得Y 的 反函数 Y 。这个规则叫做反演定理。 反演变换: “﹒”→“﹢” “﹢”→“﹒” “0” → “1” “1” →“0” , 原变量→反变量 反变量→原变量