
2.4.3对偶定理 对任何一个逻辑表达式Y作对偶变换,可的对偶 式Y。 对偶变换: Y=AB+A(C+0) Y'=(A+B)(A+C.1) 0261 613→“0 运用对偶定理时,同样应注意运算的优先顺序, 必要时可加或减扩号。 26
26 对任何一个逻辑表达式Y 作对偶变换,可Y的对偶 式Yˊ 。 2.4.3 对偶定理 运用对偶定理时,同样应注意运算的优先顺序, 必要时可加或减扩号。 ( )( 1) ( 0) = + + = + + Y A B A C Y AB A C 对偶变换: “﹒”→“﹢” “﹢”→“﹒” “0” → “1” “1” →“0
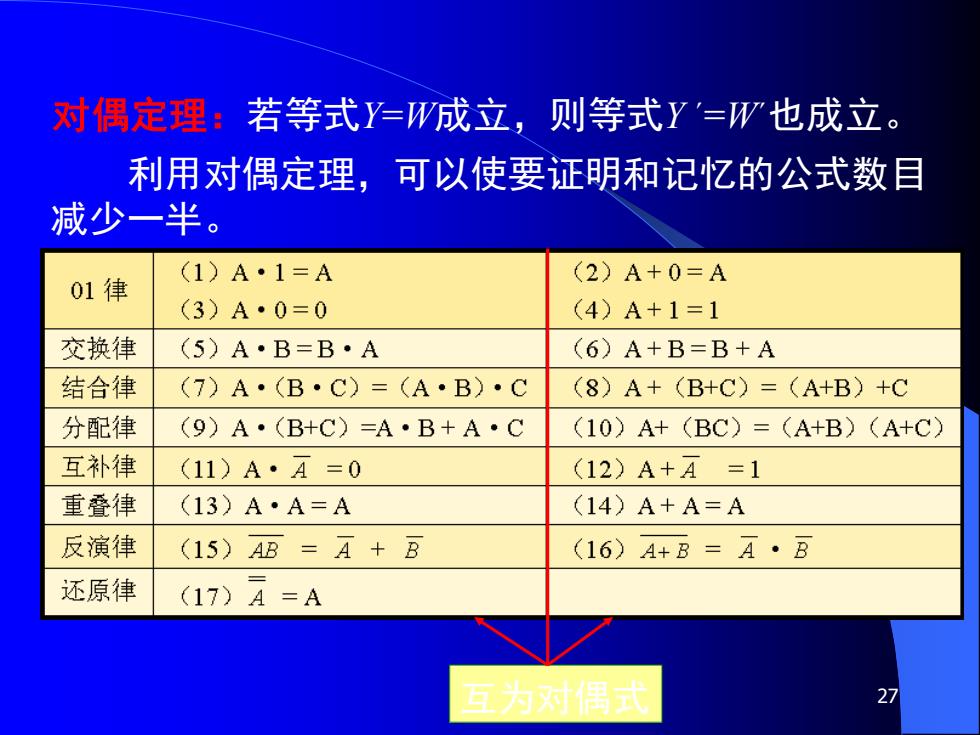
对偶定理:若等式Y=W成立,则等式Y'=W也成立。 利用对偶定理,可以使要证明和记忆的公式数目 减少一半。 (1)A·1=A (2)A+0=A 01律 (3)A·0=0 (4)A+1=1 交换律 (5)A·B=B·A (6)A+B=B+A 结合律 (7)A·(B·C)=(A·B)·C (8)A+(B+C)=(A+B)+C 分配律 (9)A·(B+C)=A·B+A·C (10)A+(BC)=(A+B)(A+C) 互补律 (11)A·A=0 (12)A+A=1 重叠律 (13)A·A=A (14)A+A=A 反演律 (15)AB=A+B (16)A+B=A·B 还原律 (17)A=A 互为对偶武 27
27 利用对偶定理,可以使要证明和记忆的公式数目 减少一半。 互为对偶式 对偶定理:若等式Y=W成立,则等式Y ˊ=Wˊ也成立
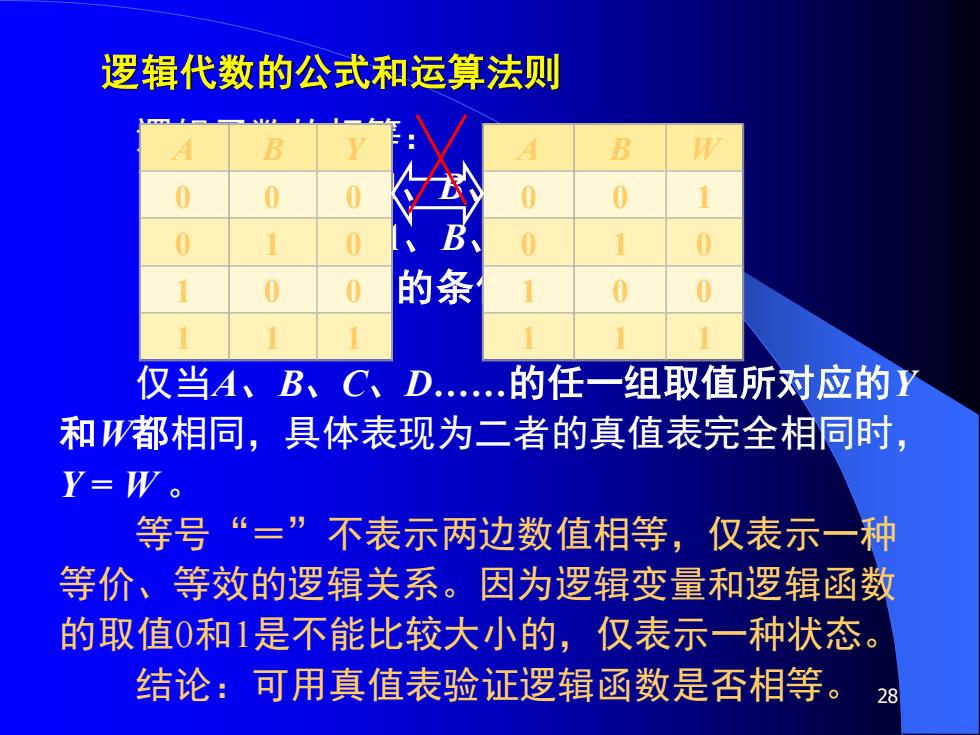
逻辑代数的公式和运算法则 B 0 0 0 B、 0 的条 0 0 1 仅当A、B、C、D.的任一组取值所对应的Y 和都相同,具体表现为二者的真值表完全相同时, Y=W。 等号“=”不表示两边数值相等,仅表示一种 等价、等效的逻辑关系。因为逻辑变量和逻辑函数 的取值0和1是不能比较大小的,仅表示一种状态。 结论:可用真值表验证逻辑函数是否相等。8
28 逻辑代数的公式和运算法则 逻辑函数的相等: 已知 Y = F1 (A、B、C、D.) W= F2 (A、B、C、D.) 问: Y = W 的条件? 仅当A、B、C、D.的任一组取值所对应的Y 和W都相同,具体表现为二者的真值表完全相同时, Y = W 。 等号“=”不表示两边数值相等,仅表示一种 等价、等效的逻辑关系。因为逻辑变量和逻辑函数 的取值0和1是不能比较大小的,仅表示一种状态。 结论:可用真值表验证逻辑函数是否相等。 A B Y 0 0 0 0 1 0 1 0 0 1 1 1 A B W 0 0 1 0 1 0 1 0 0 1 1 1

复习与思考 代入定理中对代入逻辑式的形式和复杂程度 有无限制? 。利用反演定理对逻辑式求反时,应如何处理变换的 优先顺序和式中所有的非运算符 29
29 复习与思考 ⚫ 代入定理中对代入逻辑式的形式和复杂程度 有无限制? ⚫ 利用反演定理对逻辑式求反时,应如何处理变换的 优先顺序和式中所有的非运算符

2.5逻辑函数及其表示方法 2.5.1逻辑函数 2.5.2逻辑函数及其表示方法 2.5.3逻辑函数的两种表示方法 30
30 2.5 逻辑函数及其表示方法 2.5.1 逻辑函数 2.5.2 逻辑函数及其表示方法 2.5.3 逻辑函数的两种表示方法