
2.3逻辑代数的基本公式和常用公式 2.3.1基本公式 2.3.2_若干常用公式 2.4逻辑代数的基本定律 241代入定理 242反演定理 243对偶定理 16
16 2.3 逻辑代数的基本公式和常用公式 2.3.1 基本公式 2.3.2 若干常用公式 2. 4 逻辑代数的基本定律 2. 4. 1 代入定理 2. 4. 2 反演定理 2. 4. 3 对偶定理
2,3.1基本公式 (1)常量之间的关系 这些常量之间的关 00=0 0+0=0 系,同时也体现了逻辑 0·1=0 0+1=1 代数中的基本运算规则, 也叫做公理,它是人为 10=0 1+0=1 规定的,这样规定,既 1·1= 与逻辑思维的推理一致, 0=1 =0 又与人们已经习惯了的 普通代数的运算规则相 清特别注意 似。 与普通代数 不同之处 17
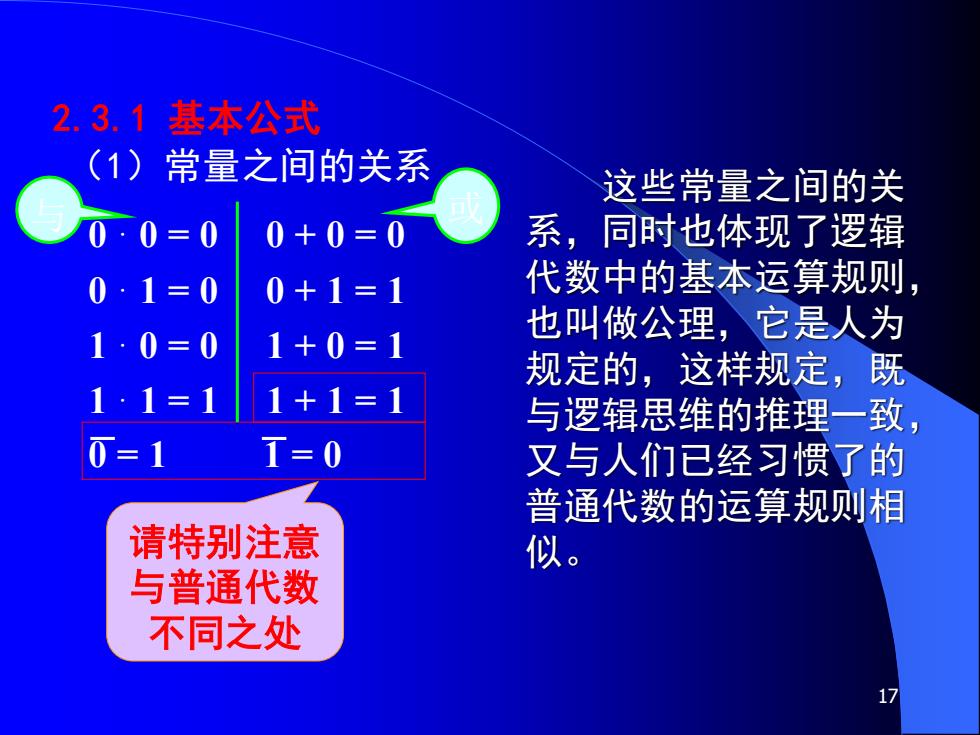
17 2.3.1 基本公式 (1)常量之间的关系 这些常量之间的关 系,同时也体现了逻辑 代数中的基本运算规则, 也叫做公理,它是人为 规定的,这样规定,既 与逻辑思维的推理一致, 又与人们已经习惯了的 普通代数的运算规则相 似。 0 ·0 = 0 0 + 0 = 0 0 ·1 = 0 0 + 1 = 1 1 ·0 = 0 1 + 0 = 1 1 ·1 = 1 1 + 1 = 1 0 = 1 1 = 0 请特别注意 与普通代数 不同之处 与 或
(2)常量与变量之间的关系 普通代数结 A+0=A A+1=1 果如何? 0-1律 A·0=0 A·1=A 同一律 A+A=AA·A=A 互补律 A+A=1 A·A=0 (3)与普通代数相似的定理 交换律 AB=BA A+B=B+A 结合律 A·(BC)=(AB) A+(B+C)=(A+B)+C 分配律 A·(B+C)=AB+AC A+(BC)=(A+B)(A+C) 18
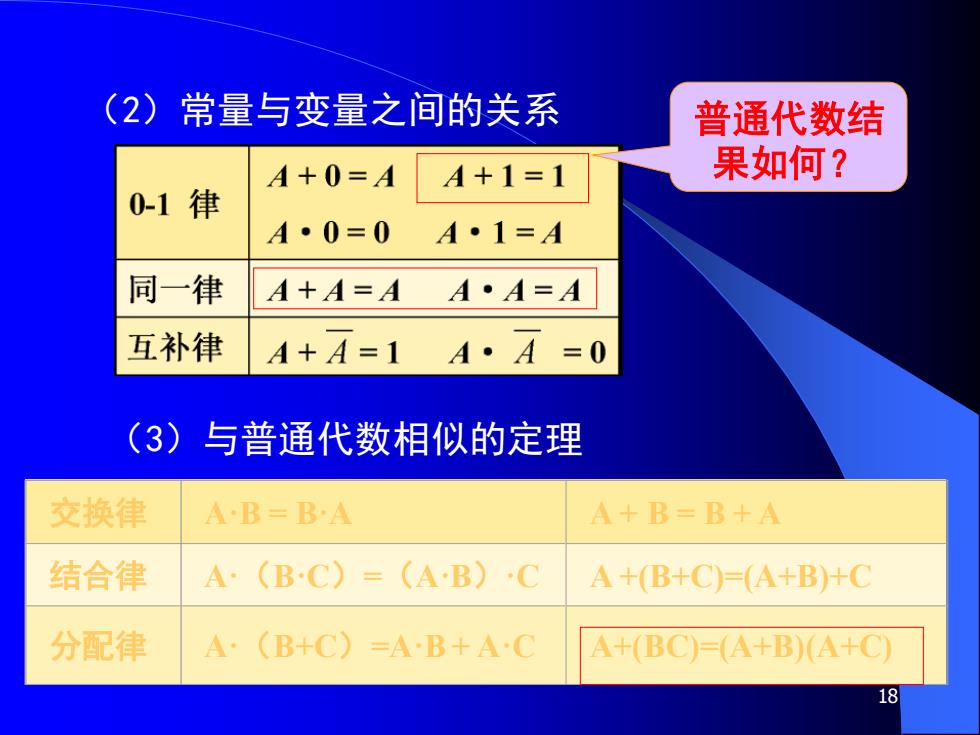
18 (2)常量与变量之间的关系 普通代数结 果如何? (3)与普通代数相似的定理 交换律 A·B = B·A A + B = B + A 结合律 A·(B·C)=(A·B)·C A +(B+C)=(A+B)+C 分配律 A·(B+C)=A·B + A·C A+(BC)=(A+B)(A+C)
(4)特殊的定理 De·mor gen AB =4+B 定理 反演律 A+B=4 B 还原律 A-A 表2-16反演律(摩根定理)真值表 A B A B AB A十B 0 0 1 1 0 0 1 1 0 0 0 0 19
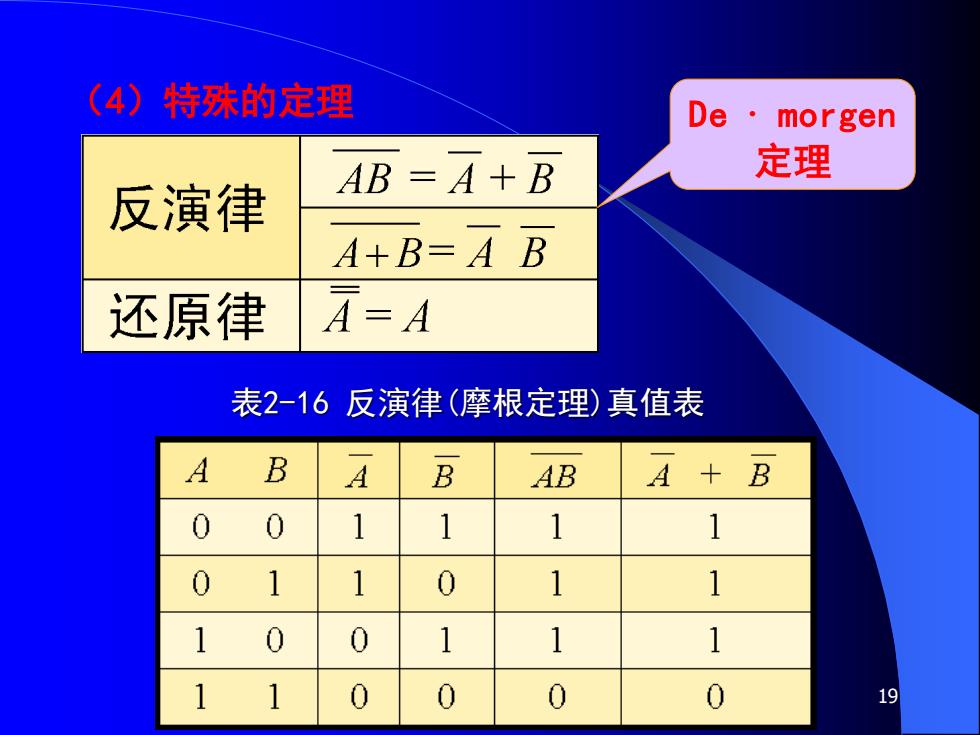
19 (4)特殊的定理 De ·morgen 定理 表2-16 反演律(摩根定理)真值表
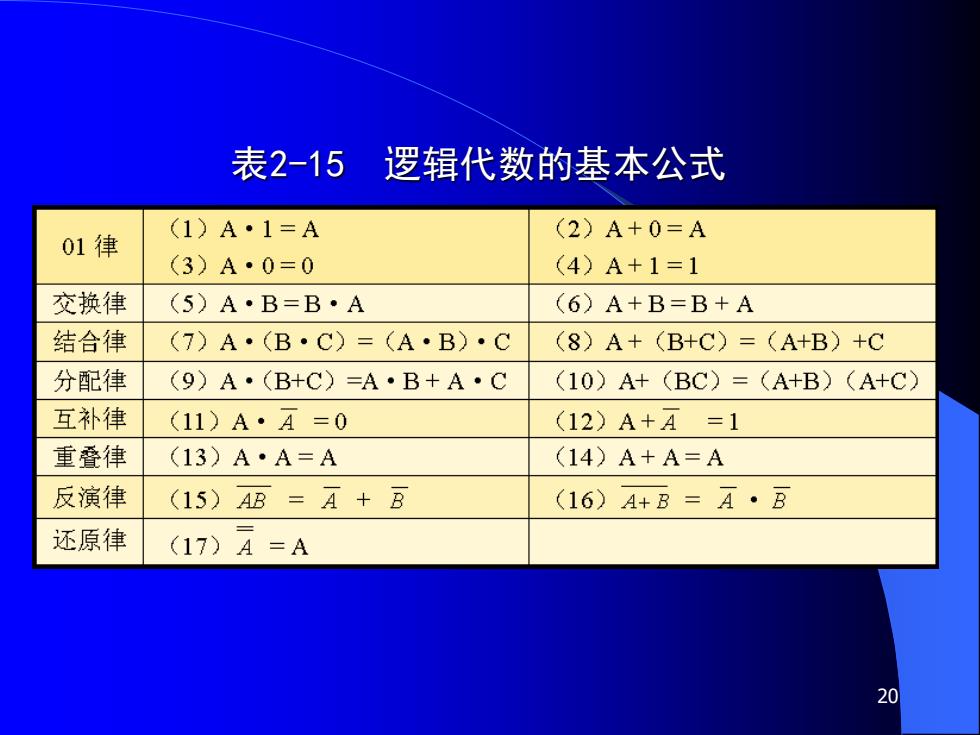
表2-15逻辑代数的基本公式 (1)A·1=A (2)A+0=A 01律 (3)A·0=0 (4)A+1=1 交换律 (5)A·B=B·A (6)A+B=B+A 结合律 (7)A·(B·C)=(A·B)·C (8)A+(B+C)=(A+B)+C 分配律 (9)A·(B+C)=A·B+A·C (10)A+(BC)=(A+B)(A+C) 互补律 (11)A·A=0 (12)A+A=1 重叠律 (13)A·A=A (14)A+A=A 反演律 (15)AB=A+B (16)A+B=A·B 还原律 (17)A=A 20
20 表2-15 逻辑代数的基本公式