
1.计算概率在假设H,为正确的条件下,根据的抽样分布算出 获得v=330kg的概率,或者说算得出现随机误差)4,=30kg) 的概率:在此,根据u测验公式可算得: 7-430-30-2 15 因为假设是新品种产量有大于或小于当地品种产量的可能 性,所以需用两尾测验。 查附表3,当u=2时,P(概率)界于0.04和0.05之间,即这 一试验结果:4=30(kg),属于抽样误差的概率小于5%
1. 计算概率 在假设 为正确的条件下,根据的抽样分布算出 获得 =330kg的概率,或者说算得出现随机误差 =30(kg) 的概率:在此,根据u 测验公式可算得: H0 y − 0 y 因为假设是新品种产量有大于或小于当地品种产量的可能 性,所以需用两尾测验。 查附表3,当u=2时,P(概率)界于0.04和0.05之间,即这 一试验结果: y − 0 =30(kg),属于抽样误差的概率小于5%。 2 15 330 300 = − = − = y y u

2.计算接受区和否定区在假设H为正确的条件下,根据)的 抽样分布划出一个区间,如)在这一区间内则接受H,如厅在 这一区间外则否定H。如何确定这一区间呢? 根据上章所述)和“=一业的分布,可知 P{u-1.96o,<<4+196o,}=0.95 P'二“>1.96y-0025p-严<196)=0.025 .P{>(u+1.966)}=0.025P<(u-1.960,)}=0.025 因此,在的抽样分布中,落在u-196o+196o) 区间内的有95%,落在这一区间外的只有5%
2. 计算接受区和否定区 在假设H0为正确的条件下,根据 的 抽样分布划出一个区间,如 在这一区间内则接受H0,如 在 这一区间外则否定H0 。 如何确定这一区间呢? y y y y y y u − 根据上章所述 和 = 的分布,可知: P{ −1.96 y y +1.96 y } = 0.95 { 1.96} = 0.025 − y y P { 1.96} = 0.025 − y y P P{y ( +1.96 y )} = 0.025 P{y ( −1.96 y )} = 0.025 因此,在 的抽样分布中,落在( ) 区间内的有95%,落在这一区间外的只有5%。 y y 96 y −1.96 , +1

如果以5%概率作为接受或否定H,的界限,则上述区间 (u一196o,u+196o,)为接受假设的区域,简称接受区 (acceptanceregion);y≤u-1.96o,和y≥u+1.96o为否定 假设的区域,简称否定区(rejection region)。 同理,若以1%作为接受或否定H的界限,则 (1-2.58o,u+2.58o,)为接受区域,D≤u-2.58o,和 ≥1+2.58o,为否定区域。 所以在测验时需先计算1.96o或2.58o,然后从加 上和减去1.96o,或2.58。,即得两个否定区域的临界值
如果以5%概率作为接受或否定H0的界限,则上述区间 ( )为接受假设的区域,简称接受区 ( acceptance region ); 和 为否定 假设的区域,简称否定区( rejection region )。 y 96 y −1.96 , +1. y y −1.96 y y +1.96 同理,若以1%作为接受或否定H0的界限,则 ( )为接受区域, 和 为否定区域。 y 58 y − 2.58 , + 2. y y − 2.58 y y + 2.58 所以在测验时需先计算1.96 或2.58 ,然后从 加 上和减去1.96 或2.58 ,即得两个否定区域的临界值。 y y y y y
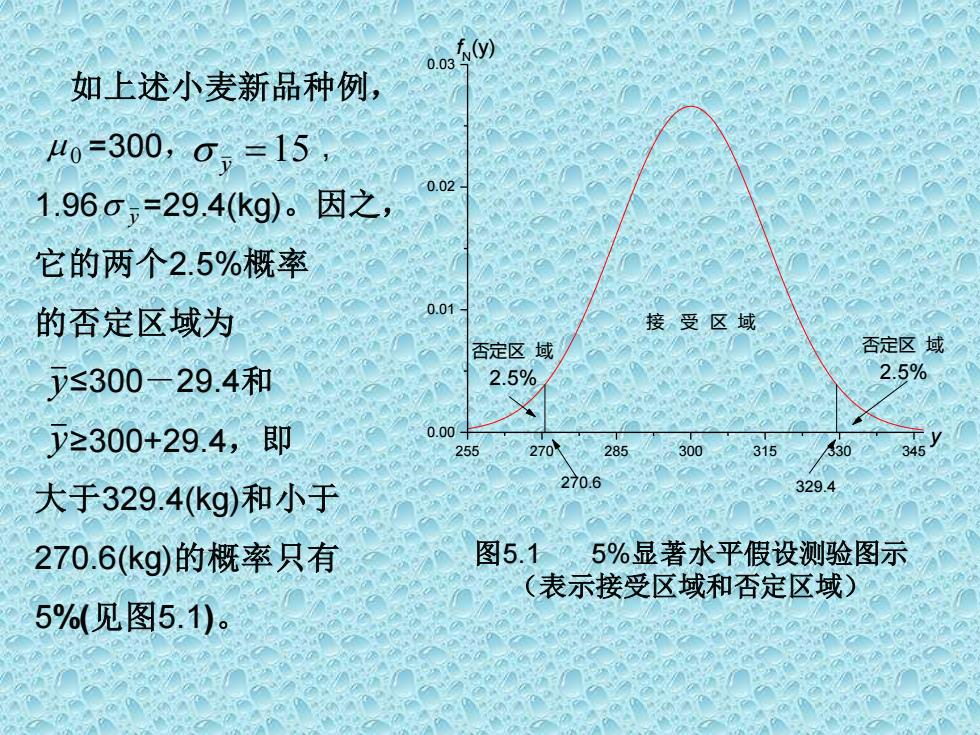
o035 如上述小麦新品种例, 40=300,0,=15 1.96o,=29.4(kg)。因之, 0.02 它的两个2.5%概率 的否定区域为 0.01 接受区域 否定区域 否定区域 ≤300-29.4和 2.5% 2.5% y≥300+29.4,即 0.00 255 270 285300 315 36 346y 大于329.4(kg)和小于 270.6 329.4 270.6(kg)的概率只有 图5.1.5%显著水平假设测验图示 (表示接受区域和否定区域) 5%(见图5.1)
255 270 285 300 315 330 345 0.00 0.01 0.02 0.03 f N (y) y 270.6 329.4 否定区 域 2.5% 否定区 域 2.5% 接 受 区 域 平均数取值 如上述小麦新品种例, =300, , 1.96 =29.4(kg)。因之, 它的两个2.5%概率 的否定区域为 ≤300-29.4和 ≥300+29.4,即 大于329.4(kg)和小于 270.6(kg)的概率只有 5%(见图5.1)。 0 y y =15 y y 图5.1 5%显著水平假设测验图示 (表示接受区域和否定区域)

(三)根据“小概率事件实际上不可能发生”原理接受或否定假设 当y一4由随机误差造成的概率小于5%或1%时,就可 认为它不可能属于抽样误差,从而否定假设。 如果因随机误差而得到某差数的概率P<0.05,则称这个 差数是显著的。如果因随机误差而得到某差数的概率P<0.01, 则称这个差数是极显著的。而这种假设测验也叫显著性测验。 用来测验假设的概率标准5%或1%等,称为显著水平 (significancelevel)。一般以表示,如=0.05或=0.01。 a 0
(三) 根据“小概率事件实际上不可能发生”原理接受或否定假设 当 由随机误差造成的概率小于5%或1%时,就可 认为它不可能属于抽样误差,从而否定假设。 如果因随机误差而得到某差数的概率P<0.05,则称这个 差数是显著的。如果因随机误差而得到某差数的概率P<0.01, 则称这个差数是极显著的。而这种假设测验也叫显著性测验。 用来测验假设的概率标准5%或1%等,称为显著水平 ( significance level )。 一般以 表示,如 =0.05或 =0.01。 y −