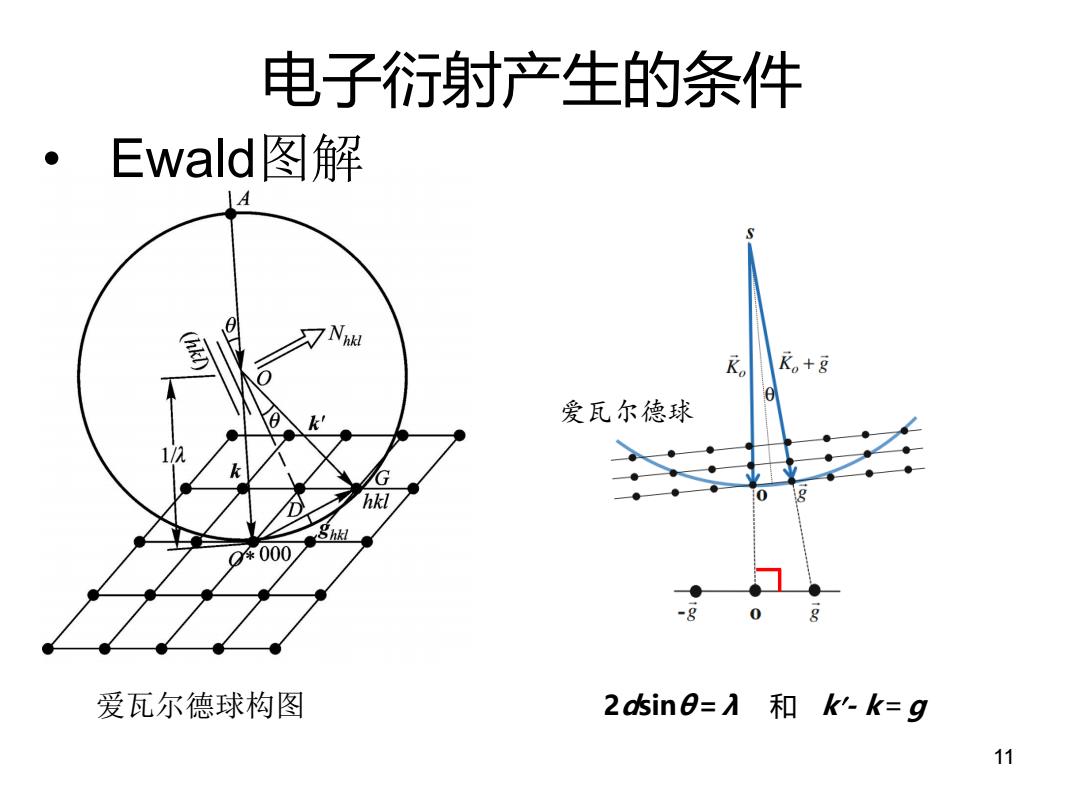
电子衍射产生的条件 Ewald图解 A 。+8 爱瓦尔德球 hkl 8h腿 000 0 爱瓦尔德球构图 2a5in8=入和k-k=g 11
爱瓦尔德球构图 11 爱瓦尔德球 2dsinθ=λ 和 k- k=g • Ewald图解 电子衍射产生的条件
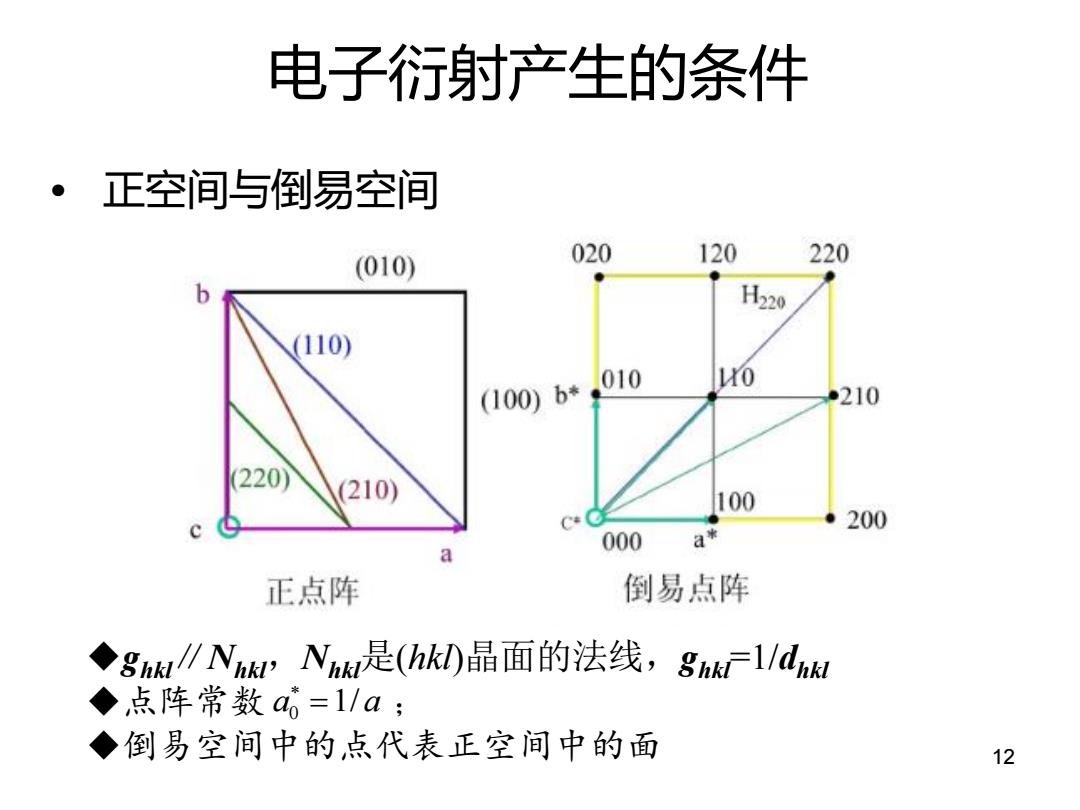
电子衍射产生的条件 ·正空间与倒易空间 (010) 020 120 220 b H220 (110) (100)b*,010 HO ●210 (220) (210) 100 200 000 a 正点阵 倒易点阵 ◆ghk∥Nh,Nhk是(hk)晶面的法线,gk广1/LhM ◆,点阵常数a=l/a; ◆倒易空间中的点代表正空间中的面 12
ghkl∥Nhkl,Nhkl是(hkl)晶面的法线,ghkl=1/dhkl 点阵常数 ; 倒易空间中的点代表正空间中的面 a0 1/ a • 正空间与倒易空间 电子衍射产生的条件 12

正空间与倒易空间 当晶体的某 (hkl)晶面满足衍射几何条件:2dsin0=或k:k=g,还必 须满足结构振幅FkM(也常用F,表示)不能等于零,也就是说一个晶胞内所 有原子的散射波在衍射方向上的合成振幅不能等于零,否则也不能产生衍射。 (hk0晶面的结构振幅及结构因子的表达式为: ∑f,e A i= |5P=FwFw=[∑os2π(应,+y,+,) +[∑”1,sn2πx,++E, 式中:是原子的散射因子,xy是原子的坐标,n是晶胞中的原子数。 13
正空间与倒易空间 当晶体的某(hkl)晶面满足衍射几何条件:2dsinθ=λ或k- k=g,还必 须满足结构振幅Fhkl(也常用 Fg表示)不能等于零,也就是说一个晶胞内所 有原子的散射波在衍射方向上的合成振幅不能等于零,否则也不能产生衍射。 (hkl)晶面的结构振幅及结构因子的表达式为: 13 n j i j e c hkl j f e A A F 1 2 1 2 1 2 * sin 2 ( ) cos2 ( ) n j j j j j n j hkl hkl hkl j j j j f h x k y lz F F F f h x k y lz 式中:f j是j原子的散射因子, xj ,yj ,zj是j原子的坐标,n是晶胞中的原子数

正空间与倒易空间 如果把那些F等于零所对应的倒易阵点从倒易点阵中去掉,借助于 倒易矢量的两个基本性质(ghM∥NhM,Nhk是(hk晶面的法线,ghk广I/LM) 不难画出:点阵常数为的简单立方正点阵的倒易点阵也是简单立方,其点 阵常数=l/a;点阵常数为a的体心立方正点阵的倒易点阵则是点阵 常数为a=2/α的面心立方点阵;而面心立方正点阵的倒易点阵则是体 心立方,其点阵常数也是a。=2/a。并且,立方正点阵的三个轴向与立 方倒易点阵是平行的。 14
正空间与倒易空间 如果把那些Fhkl等于零所对应的倒易阵点从倒易点阵中去掉,借助于 倒易矢量的两个基本性质(ghkl∥Nhkl,Nhkl是(hkl)晶面的法线,ghkl=1/dhkl) 不难画出:点阵常数为的简单立方正点阵的倒易点阵也是简单立方,其点 阵常数 ;点阵常数为 的体心立方正点阵的倒易点阵则是点阵 常数为 的面心立方点阵;而面心立方正点阵的倒易点阵则是体 心立方,其点阵常数也是 。并且,立方正点阵的三个轴向与立 方倒易点阵是平行的。 a0 1/ a a0 2/ a a0 2/ a a 14
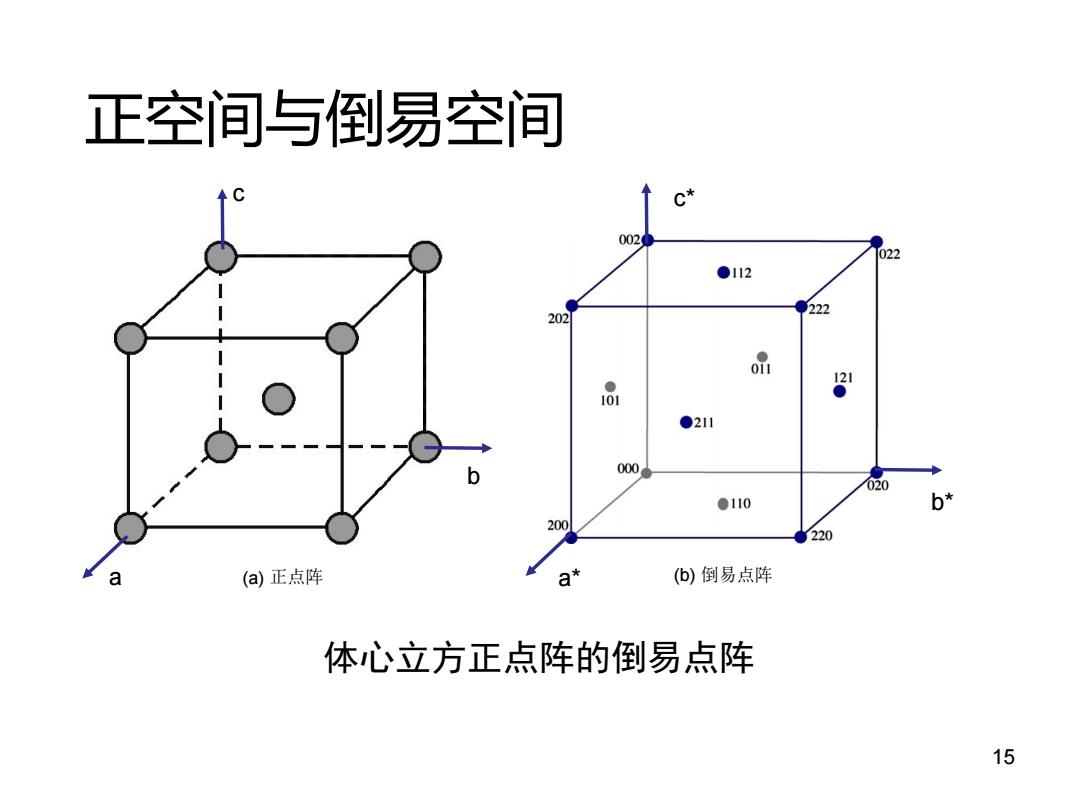
正空间与倒易空间 002 022 ●112 202 222 0品 181 ● ●211 000 020 ●110 b* 200 220 a (a)正点阵 ⊙* (b)倒易点阵 体心立方正点阵的倒易点阵 15
体心立方正点阵的倒易点阵 (a) 正点阵 (b) 倒易点阵 15 正空间与倒易空间 a b c a* b* c*