
电子衍射 晶体对电子的衍射与对X射线一样,也要满足衍射几何条件 (布拉格公式)和物理条件(结构因子),所获得的衍射花样, 对多晶体则为一系列半径不同的同心衍射环所组成,对单晶体是 一系列规则排列的衍射斑点。电子衍射和X射线衍射的相似性和 差异性的主要几方面列在下表中,其中最重要的是用于衍射的电 子波长比X射线波长短得多,导致了电子衍射角很小,使单晶电 子衍射花样在结构分析方面比X射线容易得多。 6
晶体对电子的衍射与对X射线一样,也要满足衍射几何条件 (布拉格公式)和物理条件(结构因子),所获得的衍射花样, 对多晶体则为一系列半径不同的同心衍射环所组成,对单晶体是 一系列规则排列的衍射斑点。电子衍射和X射线衍射的相似性和 差异性的主要几方面列在下表中,其中最重要的是用于衍射的电 子波长比X射线波长短得多,导致了电子衍射角很小,使单晶电 子衍射花样在结构分析方面比X射线容易得多。 电子衍射 6

电子衍射与X射线衍射的比较 相似性 差异性 1.波的叠加性导致: 1.单原子散射的特性: 布拉格公式 ():受原子核散射 结构因子 (X):受核外电子散射 消光规律 2衍射波长及衍射角: 2.衍射花样类型: (E):入=103nm, 衍射角2从0~3° 单晶花样 (X):1=10-1nm,衍射角28从0~180° 多晶花样 3.衍射斑点强度 IE/1x≈10~107 3单晶花样能确定晶体位向 4.辐射深度:(: 低于1μm数量级 ():低于100μm数量级 5.作用样品体积:(E):V≈1um3=10-9mm3 (X:V≈0.1~5mm 6晶体位向测定精度: ():用斑点花样测定,约±3° (凶:优于1° 注:()表示电子衍射,(X)表示X射线衍射
1.单原子散射的特性: (E):受原子核散射 (X):受核外电子散射 2.衍射波长及衍射角: (E):λ=10-3 nm,衍射角2θ从0~3° (X):λ=10-1 nm,衍射角2θ从0~180° 3.衍射斑点强度 4.辐射深度: (E): 低于1μm数量级 (X):低于100μm数量级 5.作用样品体积: (E): (X): 6.晶体位向测定精度: (E):用斑点花样测定,约±3° (X):优于1° 电子衍射与X射线衍射的比较 6 7 I E / I X 10 ~10 3 9 3 1μm 10 mm V 3 V 0.1~ 5mm 相 似 性 差 异 性 1.波的叠加性导致: 布拉格公式 结构因子 消光规律 2.衍射花样类型: 单晶花样 多晶花样 3.单晶花样能确定晶体位向 注:(E)表示电子衍射,(X)表示X射线衍射。 7

电子衍射产生的条件 一束波长为入的平行波入射进了一个多层平行平面结 构中,并且被散射了… 入射波 散射波 0 光程差 布拉格方程2dsin0=n) 8
8 电子衍射产生的条件 d 一束波长为的平行波入射进了一个多层平行平面结 构中,并且被散射了… 入射波 散射波 布拉格方程 2dsin = n 光程差

电子衍射产生的条件 正空间与倒易空间 布拉格公式是衍射几何条件在正空间中的表示法,爱瓦尔德球构图则是 对衍射几何条件在倒易空间中的描述。 以晶体点阵原点O为球心,以1/几为半径作球。沿平行于入射方向,从O 作入射波波矢k,并且(=1/几,其端点O*作为相应的倒易点阵的原点,该 球称为爱瓦尔德球,或称为反射球。当倒易阵点G与爱瓦尔德球面相截时, 测相应的晶面组(k0与入射束的方位必满足布拉格条件,而衍射束的方向就 是OG,或者写成衍射波的波矢k',其长度也等于爱瓦尔德球的半径1八。根 据倒易矢量定义,O*G=9,则可得: kk=g 上式就是衍射几何条件在倒易空间中的表示法。 9
布拉格公式是衍射几何条件在正空间中的表示法,爱瓦尔德球构图则是 对衍射几何条件在倒易空间中的描述。 以晶体点阵原点O为球心,以1/λ为半径作球。沿平行于入射方向,从O 作入射波波矢k,并且 |k|=1/λ,其端点O﹡作为相应的倒易点阵的原点,该 球称为爱瓦尔德球,或称为反射球。当倒易阵点G与爱瓦尔德球面相截时, 则相应的晶面组(hkl)与入射束的方位必满足布拉格条件,而衍射束的方向就 是OG,或者写成衍射波的波矢k ,其长度也等于爱瓦尔德球的半径1/λ。根 据倒易矢量定义,O*G=g,则可得: k- k=g 上式就是衍射几何条件在倒易空间中的表示法。 9 • 正空间与倒易空间 电子衍射产生的条件
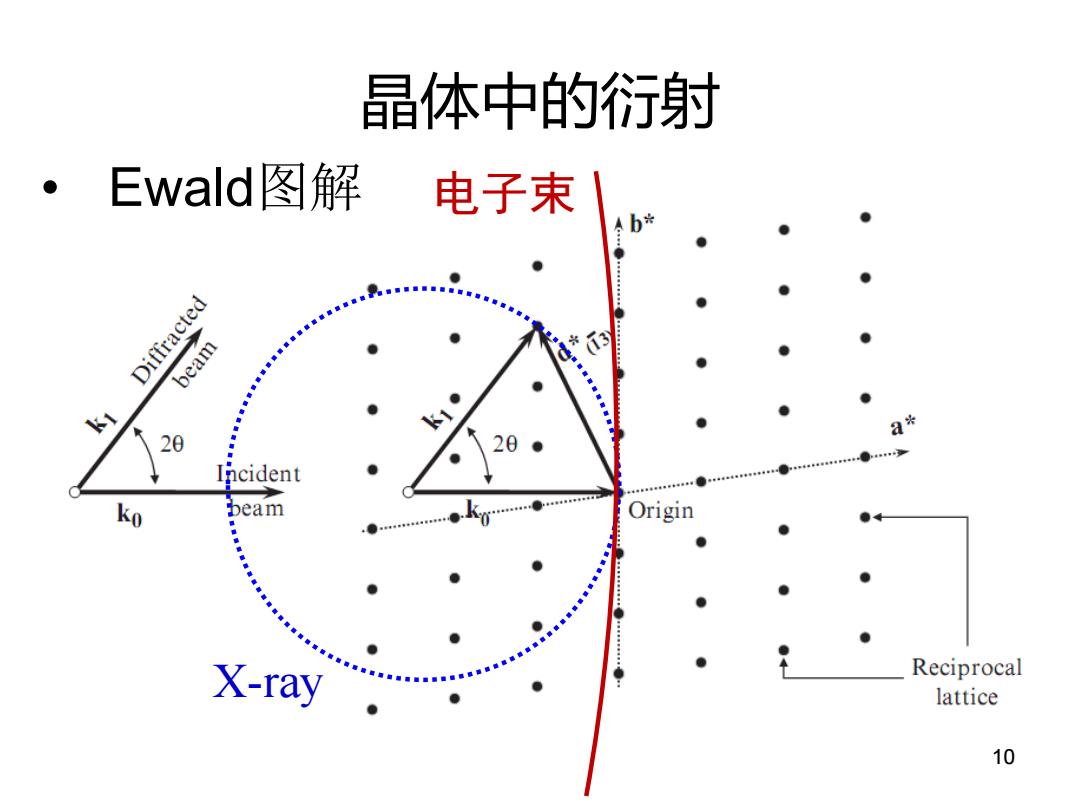
晶体中的衍射 Ewald图解 电子束 b* ● Diffracted beam : 20 Incident ko beam Origin X-ray Reciprocal lattice 10
晶体中的衍射 10 X-ray • Ewald图解 电子束