
气体分子动理论的基本公式 令:u2代表各分子在x方向上分速度平方的平均值: ∑n:∑n4 ∑% i ∑” 2 2 或 2 得: px=mnu 同理 py =mnuy p:=mnu
气体分子动理论的基本公式 或 得: 令: ux 2 代表各分子在x方向上分速度平方的平均值: 2 2 , , 2 i i x i i x i i x i i n u n u u n n = = 2 2 i i x x , i n u nu = 同理 2 p mnu x x = 2 p mnu y y = 2 p mnu z z =

气体分子动理论的基本公式 各个方向的压力应该相同,所以有 Px=Py=P:=P 从而可得: =4= 对于所有分子而言,显然应该有: ∑nG=∑n+∑n4,+∑n 上式两边同除以n,得: w心.2-++d 之
气体分子动理论的基本公式 各个方向的压力应该相同,所以有 对于所有分子而言,显然应该有: 上式两边同除以n,得: p p p p x y z = = = 222 从而可得: uuu x y z = = 2 2 2 2 i i i i x i i y i i z , , , i i i i n u n u n u n u = + + 2 2 2 2 i i i i x i i y i i z , , , i i i i n u n u n u n u n n n n = + + 222 = + + uuu x y z

气体分子动理论的基本公式 令根均方速率为: ∑n,4 =1 n 则有: 2=+4+=3 p=3mnu" 等式两边同乘以V,得: pV =mNu 3
令根均方速率u为: 则有: 等式两边同乘以V,得: 1 2 3 p mnu = 1 2 3 pV mNu = 2 i i i n u u n = 2 2 2 2 u = + + u u x y z u 2 = 3ux 气体分子动理论的基本公式

压力和温度的统计概念 单个分子在单位时间、单位体积上所引起的动 量变化是起伏不定的。但由于气体是大量分子的集 合,尽管个别分子的动量变化起伏不定,而平均压 力却是一个定值,并且是一个宏观可测的物理量。 对于一定量的气体,当温度和体积一定时, 压力具有稳定的数值。 压力是大量分子集合所产生的总效应,是 统计平均的结果
压力和温度的统计概念 单个分子在单位时间、单位体积上所引起的动 量变化是起伏不定的。但由于气体是大量分子的集 合,尽管个别分子的动量变化起伏不定,而平均压 力却是一个定值,并且是一个宏观可测的物理量。 压力p是大量分子集合所产生的总效应,是 统计平均的结果。 对于一定量的气体,当温度和体积一定时, 压力具有稳定的数值
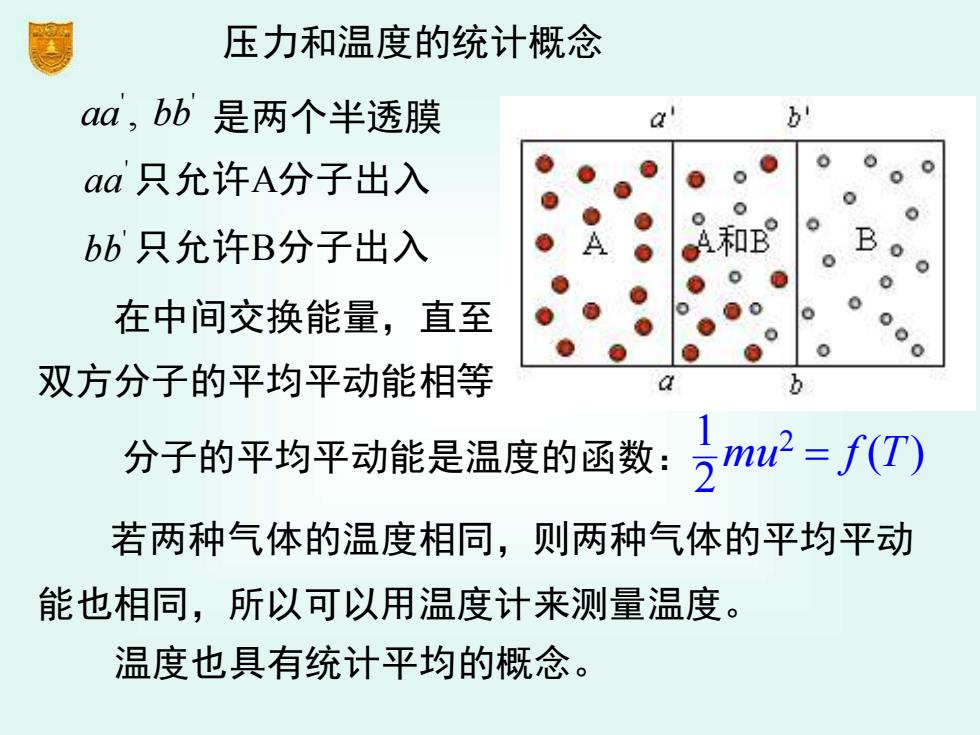
压力和温度的统计概念 aa,bb是两个半透膜 b aa只允许A分子出入 bb只允许B分子出入 A和B 在中间交换能量,直至 0 0 0 双方分子的平均平动能相等 分子的平均平动能是温度的函数:)mw2=f0) 若两种气体的温度相同,则两种气体的平均平动 能也相同,所以可以用温度计来测量温度。 温度也具有统计平均的概念
压力和温度的统计概念 是两个半透膜 ' ' aa bb , bb' 只允许B分子出入 aa ' 只允许A分子出入 在中间交换能量,直至 双方分子的平均平动能相等 分子的平均平动能是温度的函数: 1 2 ( ) 2 mu f T = 若两种气体的温度相同,则两种气体的平均平动 能也相同,所以可以用温度计来测量温度。 温度也具有统计平均的概念