
圈上海文通大学 Motion as vectors General Plane Motion(complex motion): >(Chasles'corollary to Euler's theorem) Any displacement of a rigid body is equivalent to the sum of a translation of any one point on that body and a rotation of the body about an axis through that point Total displacement translation comp.rotation comp. RB"A=RAA+RB"A RBA RM汽 RBA 国上泽充大半 OUTLINE Why kinematic analysis ©Motion as vectors Position analysis of linkages Instantaneous velocity center Applications of Instant Centers 11
11 • General Plane Motion(complex motion): (Chasles’ corollary to Euler’s theorem) Any displacement of a rigid body is equivalent to the sum of a translation of any one point on that body and a rotation of the body about an axis through that point. Total displacement = translation comp. + rotation comp. RB’’A = RA’A + RB’’A’ Motion as vectors OUTLINE Why kinematic analysis Motion as vectors Position analysis of linkages Instantaneous velocity center Applications of Instant Centers
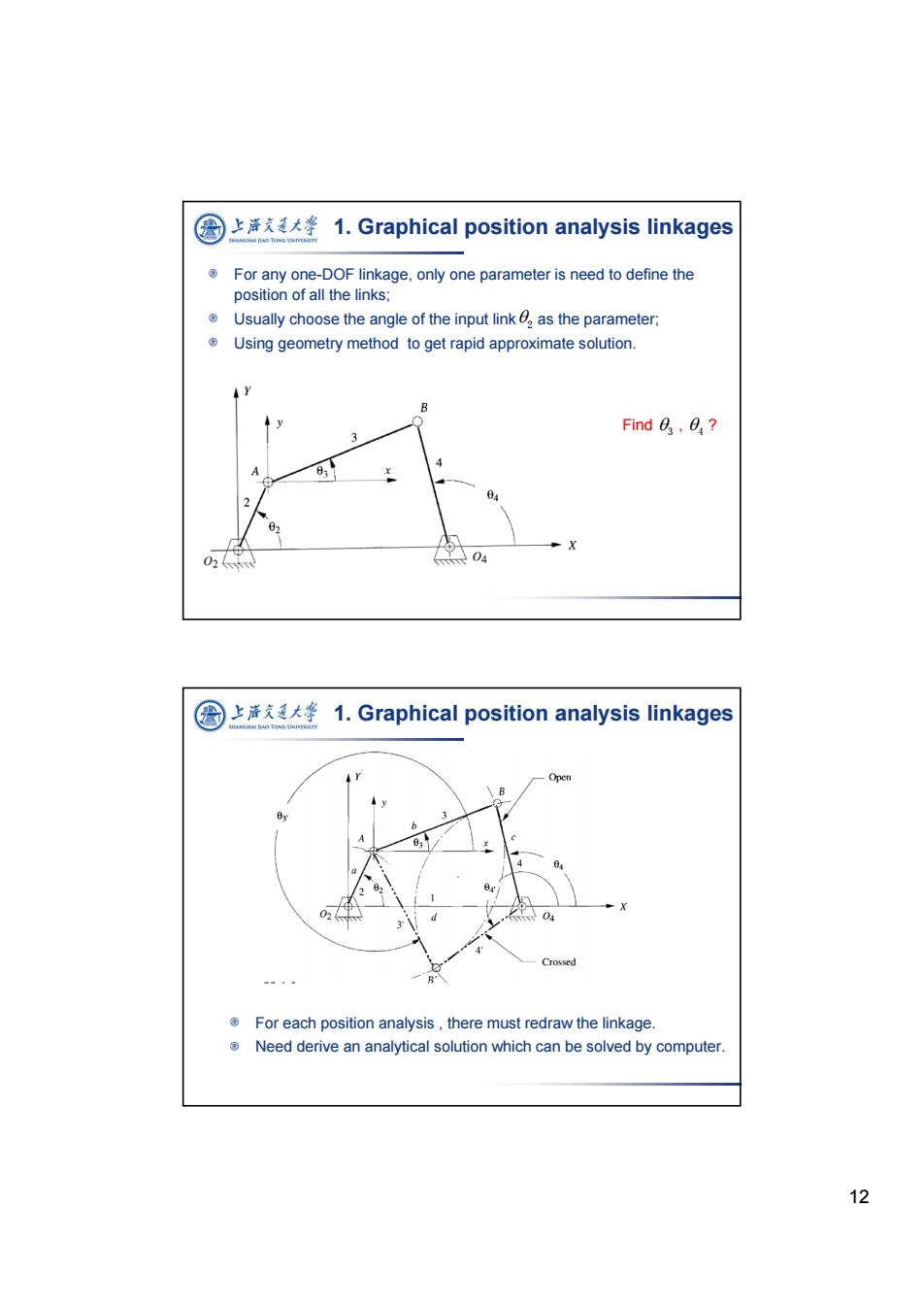
图 上谱克通大¥1.Graphical position analysis linkages For any one-DOF linkage,only one parameter is need to define the position of all the links; Usually choose the angle of the input link as the parameter; Using geometry method to get rapid approximate solution. Find 0.0? 3 2 62 04 上游充通大¥ 1.Graphical position analysis linkages Open b 024 d 04 Crossed For each position analysis,there must redraw the linkage Need derive an analytical solution which can be solved by computer. 12
12 For any one-DOF linkage, only one parameter is need to define the position of all the links; Usually choose the angle of the input link as the parameter; Using geometry method to get rapid approximate solution. 1. Graphical position analysis linkages Find , ? 3 4 2 1. Graphical position analysis linkages For each position analysis , there must redraw the linkage. Need derive an analytical solution which can be solved by computer