定义 一个排列中所有逆序的总数称为此排列的 逆序数。 例如 排列32514中, 0 逆序数为3 故此排列的逆序数为3+1+0+1+0=5
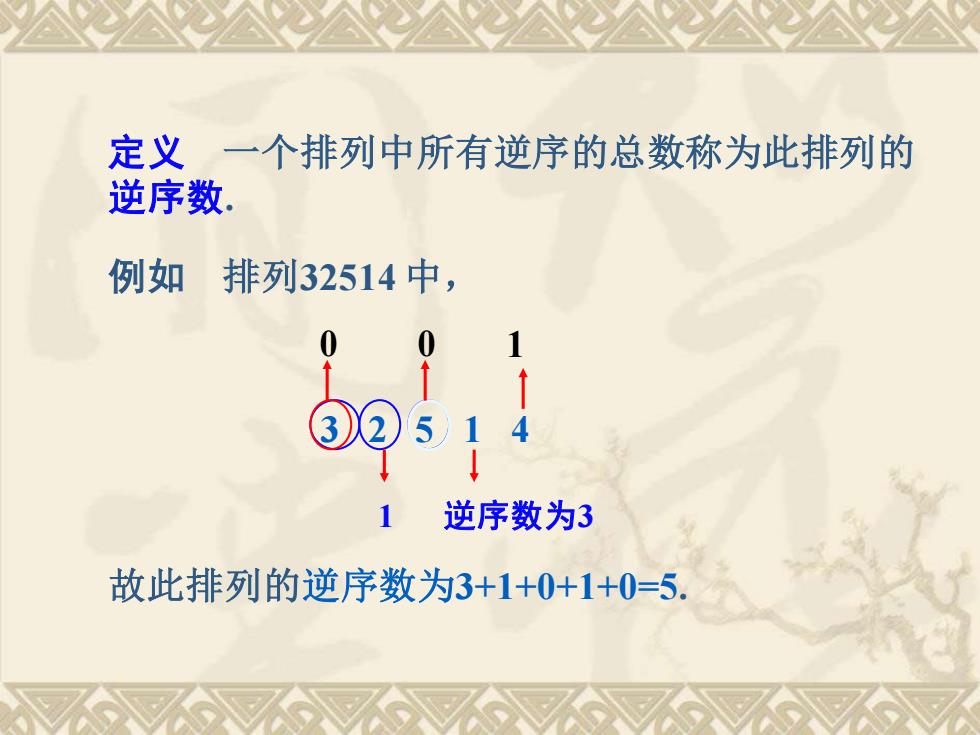
定义 一个排列中所有逆序的总数称为此排列的 逆序数. 例如 排列32514 中, 3 2 5 1 4 1 逆序数为3 0 0 1 故此排列的逆序数为3+1+0+1+0=5

排列的奇偶性 逆序数为奇数的排列称为奇排列: 逆序数为偶数的排列称为偶排列, 例如上面的排列32514的逆序数为5,它 是奇排列。 计算排列逆序数的方法 方法1 分别计算出排在1,2,.,n-1,n前面比它大的数 码之和即分别算出1,2,.,n-1,n这个元素 的逆序数,这个元素的逆序数的总和即为所求 排列的逆序数
计算排列逆序数的方法 方法1 分别计算出排在 前面比它大的数 码之和即分别算出 这 个元素 的逆序数,这个元素的逆序数的总和即为所求 排列的逆序数. 1,2, ,n −1,n 1,2, ,n −1,n n 逆序数为奇数的排列称为奇排列; 逆序数为偶数的排列称为偶排列. 排列的奇偶性 例如上面的排列32514的逆序数为5·,它 是奇排列

方法2 分别计算出排列中每个元素前面比它大的数码 个数之和(一般我们从最后一个元素开始), 即算出从最后一个开始排列中每个元素的逆序数, 这每个元素的逆序数之总和即为所求排列的逆 序数 例1 求排列32514的逆序数. 解 在排列32514中, 4的前面比4大的数有1个,故逆序数为1; 1的前面比1大的数有3个,故逆序数为3; 2的前面比2大的数只有一个3,故逆序数为1;
分别计算出排列中每个元素前面比它大的数码 个数之和(一般我们从最后一个元素开始), 即算出从最后一个开始排列中每个元素的逆序数, 这每个元素的逆序数之总和即为所求排列的逆 序数. 方法2 例1 求排列32514的逆序数. 解 在排列32514中, 2的前面比2大的数只有一个3,故逆序数为1; 4的前面比4大的数有1个,故逆序数为1; 1的前面比1大的数有3个,故逆序数为3;
5的前面没有比5大的数,其逆序数为0; 2的前面比2大的数只有一个3,故逆序数为1; 3排在首位,逆序数为0; 88 可以不用写出 于是排列32514的逆序数为 t=1+3+0+1+0=5
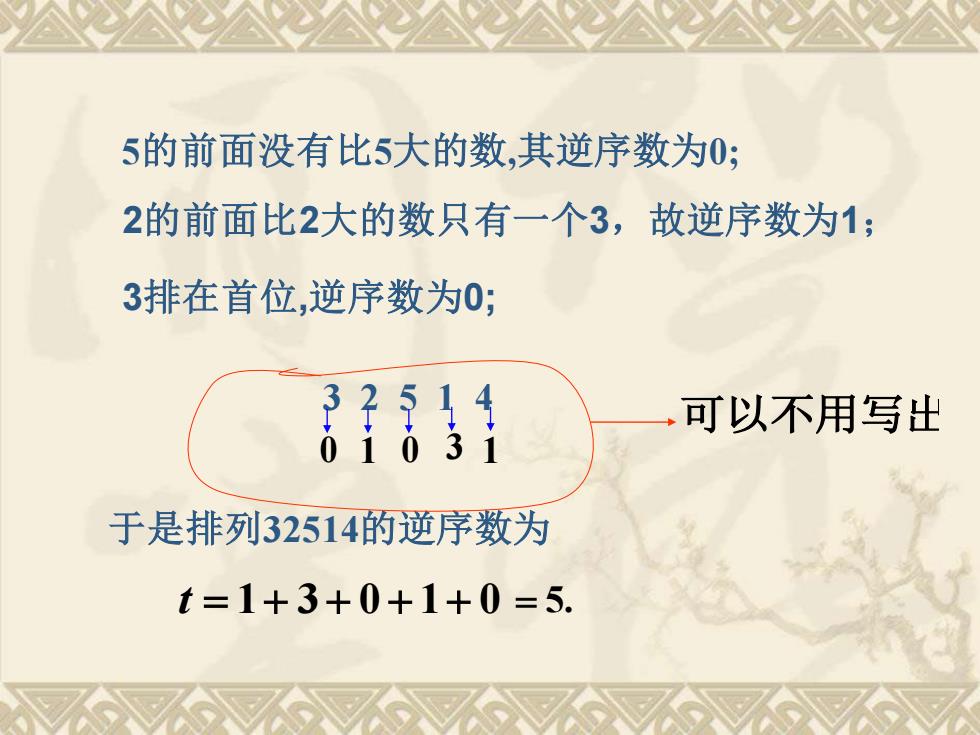
3 2 5 1 4 0 1 0 3 1 于是排列32514的逆序数为 t = 1+ 3 + 0 + 1+ 0 = 5. 5的前面没有比5大的数,其逆序数为0; 可以不用写出 3排在首位,逆序数为0; 2的前面比2大的数只有一个3,故逆序数为1;

例2计算下列排列的逆序数,并讨论它们的奇 偶性。 (0 217986354 可以不写出 解 21⑦⑨863⑤4 0iò63445 t=5+4+4+3+1+0+0+1+0 =18 此排列为偶排列
例2 计算下列排列的逆序数,并讨论它们的奇 偶性. (1) 217986354 解 2 1 7 9 8 6 3 5 4 0 1 0 0 1 3 4 4 5 t = = 18 此排列为偶排列. 5 + 4 + 4 + 3 + 1 + 0 + 0 + 1 + 0 可以不写出