
目录 第一章拉普拉斯变换(Laplace Transform)的应用案例.,l §1.1一阶电路的零输入响应. .1 §1.2一阶电路的零状态响应与全响应.2 §13二阶电路的零输入响应.6 51.4二阶电路的零状态响应和全响应.9 §1.5一阶电路和二阶电路的阶跃响应.11 §1.6一阶电路和二阶电路的冲激响应.12 §1.7运算电路综合.13 第二章电路基础知识介绍.18 §2.1运算电路基础知识.18 2.2运算电路举例.20 参考文献
目 录 第一章 拉普拉斯变换(Laplace Transform)的应用案例 . 1 §1.1 一阶电路的零输入响应 . 1 §1.2 一阶电路的零状态响应与全响应 . 2 §1.3 二阶电路的零输入响应 . 6 §1.4 二阶电路的零状态响应和全响应 . 9 §1.5 一阶电路和二阶电路的阶跃响应 . 11 §1.6 一阶电路和二阶电路的冲激响应 . 12 §1.7 运算电路综合 . 13 第二章 电路基础知识介绍 . 18 §2.1 运算电路基础知识 . 18 §2.2 运算电路举例 . 20 参考文献. 22

第一章拉普拉斯变换(Laplace Transform)的应用案例 Laplace Transform的目的:利用电路的复频域模型直接列出复频域方程,从 而求得所需相应的象函数F(s),再通过Laplace Transform反变换求得电路的时域 响应f0.避免了建立电路的微分方程和确定电路的初始条件的过程。 §1.1一阶电路的零输入响应 案例1.1.1如图1-1-1所示电路中,开关S闭合前,电容已充电,其电压= U。开关闭合后,电容存储的能量将通过热能形式释放出来,把开关闭合时刻取为 (t=0),求开关闭合后(t≥0)时u (t=0 解:根据k(基尔霍夫电压定律)得: uR-uc=0 u=Ri,i=-C警(电容放电警≤0 代入方程得: RC+uc=0,初始条件uc(O)=Uo, 使用拉普拉斯变换求解: 图1-1-1RC电路的零输入响应 设u=Us,则=sU)-o 对方程两边同取拉普拉斯变换得: RG6US)-0)+U=0整理得:U6)=器=是 取拉式逆变换得:c=Uoe心, GeoGebra软件运算区求解 方法一:使用solveode(RC·y+y=0,(O,Uo),解得y=Uoec 方法二:使用iere(器小解得逆变换为U,e元 注:solveode解一阶微分方程默认函数为y,自变量为x.求完解替换为原来的 变量。inverselaplace默认自变量为s,求完解替换为原来得自变量。 .1
- 1 - 第一章 拉普拉斯变换(Laplace Transform)的应用案例 Laplace Transform 的目的:利用电路的复频域模型直接列出复频域方程,从 而求得所需相应的象函数 F(s),再通过 Laplace Transform 反变换求得电路的时域 响应 f(t).避免了建立电路的微分方程和确定电路的初始条件的过程。 §1.1 一阶电路的零输入响应 案例 1.1.1 如图 1-1-1 所示电路中,开关 S 闭合前,电容已充电,其电压𝑢𝑐 = 𝑈0.开关闭合后,电容存储的能量将通过热能形式释放出来,把开关闭合时刻取为 (t = 0),求开关闭合后(t ≥ 0)时𝑢𝑐 . 解:根据 kvl(基尔霍夫电压定律)得: 𝑢𝑅 − 𝑢𝐶 = 0 𝑢𝑅 = 𝑅𝑖, 𝑖 = −𝐶 𝑑𝑢𝐶 𝑑𝑡 (电容放电𝑑𝑢𝐶 𝑑𝑡 ≤ 0). 代入方程得: RC 𝑑𝑢𝐶 𝑑𝑡 + 𝑢𝐶 = 0,初始条件𝑢𝐶 (0) = 𝑈0, 使用拉普拉斯变换求解: 图 1-1-1 RC 电路的零输入响应 设ℒ[𝑢𝐶 ] = 𝑈(𝑠),则 ℒ [ 𝑑𝑢𝐶 𝑑𝑡 ] = 𝑠𝑈(𝑠) − 𝑈0. 对方程两边同取拉普拉斯变换得: 𝑅𝐶(𝑠𝑈(𝑠) − 𝑈0 ) + 𝑈(𝑠) = 0,整理得:U(s) = 𝑅𝐶𝑈0 𝑅𝐶𝑠+1 = 𝑈0 𝑠+ 1 𝑅𝐶 , 取拉式逆变换得:𝑢𝐶 = 𝑈0𝑒 − 𝑡 𝑅𝐶. GeoGebra 软件运算区求解: 方法一:使用 solveode(RC ∙ 𝑦 ′ + 𝑦 = 0, (0,𝑈0)),解得 y=𝑈0𝑒 − 𝑥 𝑅𝐶. 方法二:使用 inverselaplace( 𝑅𝐶𝑈0 𝑅𝐶∙𝑠+1 , 𝑠),解得逆变换为𝑈0𝑒 − 𝑠 𝑅𝐶. 注:solveode 解一阶微分方程默认函数为 y,自变量为𝑥.求完解替换为原来的 变量。inverselaplace 默认自变量为 s, 求完解替换为原来得自变量
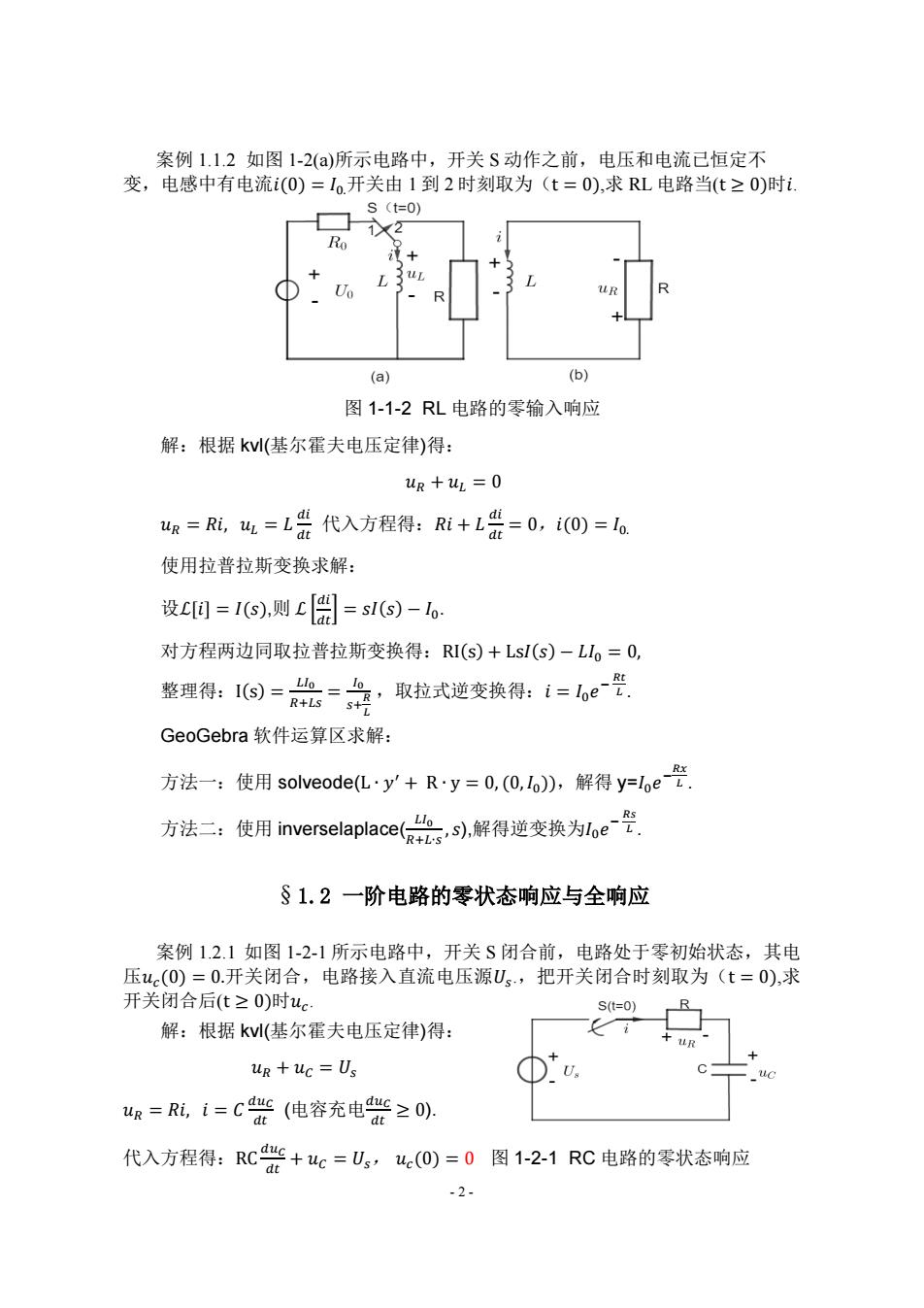
案例1.12如图1-2(a)所示电路中,开关S动作之前,电压和电流已恒定不 变,电感中有电流i(0)=1开关由1到2时刻取为(t=0),求RL电路当(t≥0)时i 0 (a) (b) 图1-1-2RL电路的零输入响应 解:根据k(基尔霍夫电压定律)得: R+4=0 4R=Ri,4=L票代入方程得:Ri+L票=0,(0)=6 使用拉普拉斯变换求解: 设0=1则c周=s1)-6 对方程两边同取拉普拉斯变换得:RI(s)+Ls(s)-Ll,=0, 整理得:1回=总=品,取拉式逆变换得:1=6e是 GeoGebra软件运算区求解: 方法一:使用solveode(Ly+Ry=0,(0,lb,解得y=1e空 方法二:使用inverselace(,s),解得逆变换为loe空 §1.2一阶电路的零状态响应与全响应 案例1.2.1如图12-1所示电路中,开关S闭合前,电路处于零初始状态,其电 压uc(0)=0.开关闭合,电路接入直流电压源U。,把开关闭合时刻取为(t=0),求 开关闭合后(t≥0)时u 解:根据k(基尔霍夫电压定律)得: uR+uc=Us D MR=Ri,i=C晋(电容充电警20), 代入方程得:RC警+“c=U,“(O)=0图1-21RC电路的零状态响应 .2
- 2 - 案例 1.1.2 如图 1-2(a)所示电路中,开关 S 动作之前,电压和电流已恒定不 变,电感中有电流𝑖(0) = 𝐼0.开关由 1 到 2 时刻取为(t = 0),求 RL 电路当(t ≥ 0)时𝑖. 图 1-1-2 RL 电路的零输入响应 解:根据 kvl(基尔霍夫电压定律)得: 𝑢𝑅 + 𝑢𝐿 = 0 𝑢𝑅 = 𝑅𝑖, 𝑢𝐿 = 𝐿 𝑑𝑖 𝑑𝑡 代入方程得:𝑅𝑖 + 𝐿 𝑑𝑖 𝑑𝑡 = 0,𝑖(0) = 𝐼0. 使用拉普拉斯变换求解: 设ℒ[𝑖] = 𝐼(𝑠),则 ℒ [ 𝑑𝑖 𝑑𝑡] = 𝑠𝐼(𝑠) − 𝐼0. 对方程两边同取拉普拉斯变换得:RI(s) + Ls𝐼(𝑠) − 𝐿𝐼0 = 0, 整理得:I(s) = 𝐿𝐼0 𝑅+𝐿𝑠 = 𝐼0 𝑠+ 𝑅 𝐿 ,取拉式逆变换得:𝑖 = 𝐼0𝑒 − 𝑅𝑡 𝐿 . GeoGebra 软件运算区求解: 方法一:使用 solveode(L ∙ 𝑦 ′ + R ∙ y = 0, (0,𝐼0)),解得 y=𝐼0𝑒 − 𝑅𝑥 𝐿 . 方法二:使用 inverselaplace( 𝐿𝐼0 𝑅+𝐿∙𝑠 , 𝑠),解得逆变换为𝐼0𝑒 − 𝑅𝑠 𝐿 . §1.2 一阶电路的零状态响应与全响应 案例 1.2.1 如图 1-2-1 所示电路中,开关 S 闭合前,电路处于零初始状态,其电 压𝑢𝑐(0) = 0.开关闭合,电路接入直流电压源𝑈𝑠 .,把开关闭合时刻取为(t = 0) ,求 开关闭合后(t ≥ 0)时𝑢𝑐 . 解:根据 kvl(基尔霍夫电压定律)得: 𝑢𝑅 + 𝑢𝐶 = 𝑈𝑠 𝑢𝑅 = 𝑅𝑖, 𝑖 = 𝐶 𝑑𝑢𝐶 𝑑𝑡 (电容充电𝑑𝑢𝐶 𝑑𝑡 ≥ 0). 代入方程得:RC 𝑑𝑢𝐶 𝑑𝑡 + 𝑢𝐶 = 𝑈𝑠, 𝑢𝑐(0) = 0 图 1-2-1 RC 电路的零状态响应

使用拉普拉斯变换求解: 设cucl=U(s),则c[=sUs)-0, 对方程两边同取拉普拉斯变换得:RCsU(S)+U(S)=号 整理得:U回=兰取拉式逆变换得:4e=心,-U,e元 GeoGebra软件运算区求解: 方法一:使用solveode(RCy+y-U,=0,(0,0),解得y=U,-U,et 方法二:使用ver(mc·兰)解得逆变换为,-山e定 当一个非零初始状态的一阶电路受到激励时,电路的响应称为一阶电路的全 响应。 案例12.2如图1-2-2所示电路中,已充电的电容经过电阻接到直流电压源U。 电容原有电压uc(0)=Uo开关闭合,把开关闭 合时刻取为(t=0),求开关闭合后(t>0)时ue 解:根据kw(基尔霍夫电压定律)得: uR+uc=Us 4R=R旺,i=C警(电容充电警≥0). 代入方程得:RC+c=U,e(0)=U。图1-2-2RC电路的全响应 使用拉普拉斯变换求解: 设u=Us),则=sUs)- 对方程两边同取拉普拉斯变换得:RC(sU(s)-Uo)+U(s)= 整理得:U囹=华+RCU) 取拉式逆变换得:c=U,+(Uo-U)e配. GeoGebra软件运算区求解: 方法一:使用solveode(RCy+y-Us=0,(0,Uo), 解得y=U+Uoe-U,e. 3
- 3 - 使用拉普拉斯变换求解: 设ℒ[𝑢𝐶 ] = 𝑈(𝑠),则 ℒ [ 𝑑𝑢𝐶 𝑑𝑡 ] = 𝑠𝑈(𝑠) − 0. 对方程两边同取拉普拉斯变换得:𝑅𝐶𝑠𝑈(𝑠) + 𝑈(𝑠) = 𝑈𝑠 𝑠 整理得:U(s) = 1 (𝑅𝐶𝑠+1) ∙ 𝑈𝑠 𝑠 取拉式逆变换得: 𝑢𝐶 = 𝑈𝑠 − 𝑈𝑠𝑒 − 𝑡 𝑅𝐶. GeoGebra 软件运算区求解: 方法一:使用 solveode(𝑅𝐶𝑦 ′ + 𝑦 − 𝑈𝑠 = 0, (0,0)),解得 y=𝑈𝑠 − 𝑈𝑠𝑒 − 𝑥 𝑅𝐶. 方法二:使用 inverselaplace( 1 (𝑅𝐶∙𝑠+1) ∙ 𝑈𝑠 𝑠 , 𝑠),解得逆变换为𝑈𝑠 − 𝑈𝑠𝑒 − 𝑠 𝑅𝐶. 当一个非零初始状态的一阶电路受到激励时,电路的响应称为一阶电路的全 响应。 案例 1.2.2 如图 1-2-2 所示电路中,已充电的电容经过电阻接到直流电压源𝑈𝑠。 电容原有电压𝑢𝑐(0) = U0.开关闭合,把开关闭 合时刻取为(t = 0),求开关闭合后(t > 0)时𝑢𝑐 . 解:根据 kvl(基尔霍夫电压定律)得: 𝑢𝑅 + 𝑢𝐶 = 𝑈𝑠 𝑢𝑅 = 𝑅𝑖, 𝑖 = 𝐶 𝑑𝑢𝐶 𝑑𝑡 (电容充电𝑑𝑢𝐶 𝑑𝑡 ≥ 0). 代入方程得:RC 𝑑𝑢𝐶 𝑑𝑡 + 𝑢𝐶 = 𝑈𝑠, 𝑢𝑐(0) = U0 图 1-2-2 RC 电路的全响应 使用拉普拉斯变换求解: 设ℒ[𝑢𝐶 ] = 𝑈(𝑠),则 ℒ [ 𝑑𝑢𝐶 𝑑𝑡 ] = 𝑠𝑈(𝑠) − U0. 对方程两边同取拉普拉斯变换得:𝑅𝐶(𝑠𝑈(𝑠) − U0) + 𝑈(𝑠) = 𝑈𝑠 𝑠 整理得:U(s) = 1 (𝑅𝐶𝑠+1) ∙ ( 𝑈𝑠 𝑠 + 𝑅𝐶U0) 取拉式逆变换得: 𝑢𝐶 = 𝑈𝑠 + (U0 − 𝑈𝑠)𝑒 − 𝑡 𝑅𝐶. GeoGebra 软件运算区求解: 方法一:使用 solveode(𝑅𝐶𝑦 ′ + 𝑦 − 𝑈𝑠 = 0, (0, U0)), 解得 y=𝑈𝑠 + U0𝑒 − 𝑥 𝑅𝐶 − 𝑈𝑠𝑒 − 𝑥 𝑅𝐶

方法二:使用inverselaplace(c*n学+RCUo,s) 解得逆变换为U,+Uoe屁-U,eC 案例123如图1-2-3所示电路中,开关S打开前,电感中电流为零。开关打 开后,(0)=0,直流电流源1,求开关打开后(t≥0)时uc 解:根据k(基尔霍夫电流定律)得: in +in=Is R=专票代入方程得: TS(t=0) +i2=1,z0)=0 使用拉普拉斯变换求解: 图1-2-3RL电路的零状态响应 设[=1s,则c[=s1(o)-0 对方程两边同取拉普拉斯变换得:片s·1(s)+1(s)=名 整理得:1因=台,取拉式逆变换得=,(1-e曾) GeoGebra软件运算区求解: 方法一:使用solveode(始y+y-1,=0,0,0),解得y以,(1-e) 方法二:使用invers(告s)解得l,(1-e宁) 案例1.2.4如图1-2-4所示电路中,直流电压源U,直流电流源1,电感L,电阻 R,试求S闭合后电路中的电流i和i, 解:开关断开时,电感L中电流 R S(t=0) i(0)=-ls 开关闭合时,根据结点电压法: Uab=-山-i+g,Ub=4, 4=L%代入上式得,且方程两边同乘R: 图1-2-4 L驶+R,+R-U,=0,i红0)=-l .4
- 4 - 方法二:使用 inverselaplace( 1 (𝑅𝐶∙𝑠+1) ∙ ( 𝑈𝑠 𝑠 + 𝑅𝐶U0), 𝑠), 解得逆变换为𝑈𝑠 + U0𝑒 − 𝑠 𝑅𝐶 − 𝑈𝑠𝑒 − 𝑠 𝑅𝐶. 案例 1.2.3 如图 1-2-3 所示电路中,开关 S 打开前,电感中电流为零。开关打 开后𝑖𝐿(0) = 0,直流电流源𝐼𝑠,求开关打开后(t ≥ 0)时𝑢𝑐 . 解:根据 kvl(基尔霍夫电流定律)得: 𝑖𝑅 + 𝑖𝐿 = 𝐼𝑠 𝑖𝑅 = 𝐿 𝑅 ∙ 𝑑𝑖𝐿 𝑑𝑡 ,代入方程得: 𝐿∙𝑑𝑖𝐿 𝑅𝑑𝑡 + 𝑖𝐿 = 𝐼𝑠 , 𝑖𝐿(0) = 0. 使用拉普拉斯变换求解 : 图 1-2-3 RL 电路的零状态响应 设ℒ[ 𝑖𝐿 ] = 𝐼(𝑠),则 ℒ [ 𝑑𝑖𝐿 𝑑𝑡 ] = 𝑠𝐼(𝑠) − 0 对方程两边同取拉普拉斯变换得: 𝐿 𝑅 𝑠 ∙ 𝐼(𝑠) + 𝐼(𝑠) = 𝐼𝑠 𝑠 , 整理得:I(s) = 1 (𝐿𝑠+1) ∙ 𝐼𝑠 𝑠 , 取拉式逆变换得𝑖𝐿 = 𝐼𝑠 (1 − 𝑒 − 𝑅𝑡 𝐿 ). GeoGebra 软件运算区求解: 方法一:使用 solveode(L 𝑅 ∙ 𝑦 ′ + y − 𝐼𝑠 = 0, (0,0)),解得 y=𝐼𝑠 (1 − 𝑒 − 𝑅𝑥 𝐿 ). 方法二:使用 inverselaplace( 1 (𝐿𝑠+1) ∙ 𝐼𝑠 𝑠 , 𝑠), 解得𝐼𝑠 (1 − 𝑒 − 𝑅𝑠 𝐿 ) 案例 1.2.4 如图 1-2-4 所示电路中,直流电压源𝑈𝑠,直流电流源𝐼𝑠,电感 L,电阻 R,试求 S 闭合后电路中的电流𝑖𝐿和𝑖. 解:开关断开时,电感 L 中电流 𝑖𝐿 (0) = −𝐼𝑠 . 开关闭合时,根据结点电压法: 1 𝑅 𝑈𝑎𝑏 = −𝐼𝑠 − 𝑖𝐿 + 𝑈𝑠 𝑅 ,𝑈𝑎𝑏 = 𝑢𝐿 , 𝑢𝐿 = 𝐿 𝑑𝑖𝐿 𝑑𝑡 ,代入上式得,且方程两边同乘 R: 图 1-2-4 𝐿 𝑑𝑖𝐿 𝑑𝑡 + 𝑅𝐼𝑠 + 𝑅𝑖𝐿 − 𝑈𝑠 = 0, 𝑖𝐿 (0) = −𝐼𝑠