P87例4-4 iR1 A is R3 B is Rs 哥 求各支路电流。 22 ↓i222i422 先用“倒退法” 120V Ro 设i5='s=1A us 202 202 202 得u's=33.02V C 再用齐性定理修正: i=K'1≈12.39A 120 i2=Ki')≈4.76A 将u's增大K= 33.02 i3=Ki3≈7.63A 倍,各支路电流将同 i4=Ki'4≈4.00A 时增大K≈3.634倍。 i5=Ki'5≈3.63A 2010年3月3日星期三 11
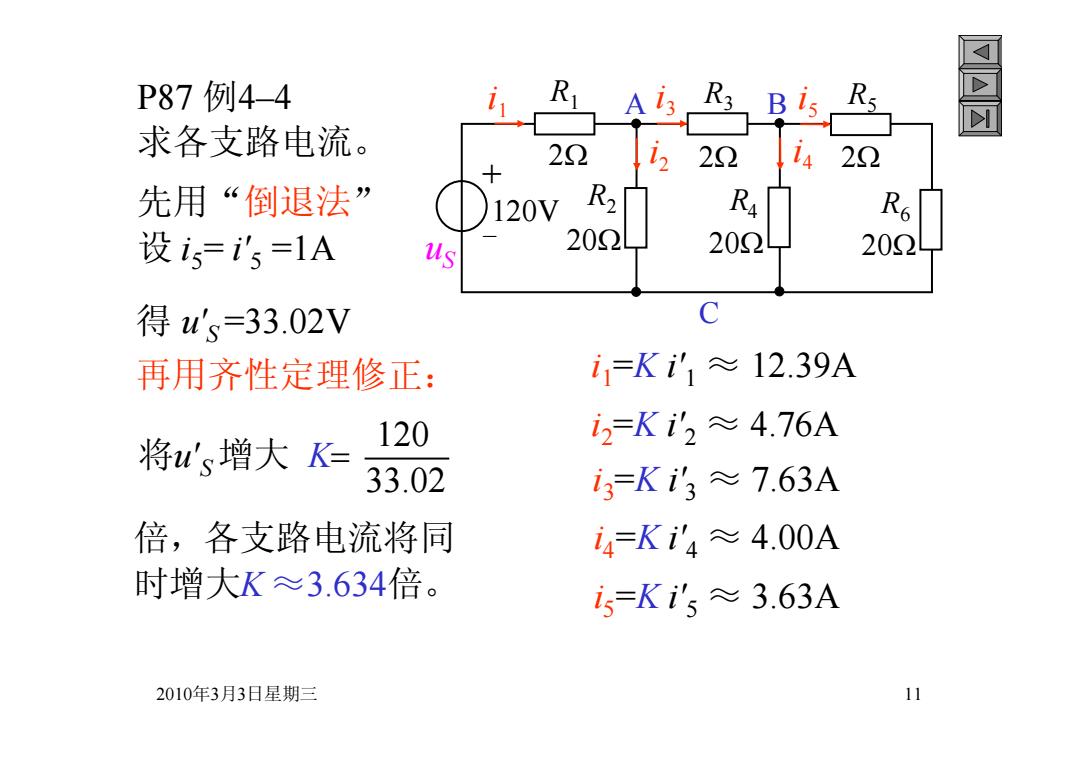
2010年3月3日星期三 11 P87 例4–4 求各支路电流。 先用“倒退法” 设 i5 = i'5 =1A 得 u'S =33.02V 再用齐性定理修正: + - 120V R1 R2 i 2 2 i 1 u 20 S R3 2 i 3 i 4 R4 20 R5 2 i 5 R6 20 A B C 将u'S增大 K 120 33.02 倍,各支路电流将同 时增大K ≈3.634倍。 i1 =K i'1 ≈ 12.39A i2 =K i'2 ≈ 4.76A i3 =K i'3 ≈ 7.63A i4 =K i'4 ≈ 4.00A i5 =K i'5 ≈ 3.63A

§4-2替代定理 昌 ·给定一个线性电阻电路,若第k条支路的电压 w,和电流为己知,那么这条支路就可以用下 列任何一个元件去替代: (1)电压等于w,的独立电压源; (2)电流等于k的独立电流源: d风管等于 的电阻。 ·替代后,该电路中其余部分的 电压和电流均保持不变。 2010年3月3日星期三 12
2010年3月3日星期三 12 §4-2 替代定理 • 给定一个线性电阻电路,若第k条支路的电压 uk和电流i k为已知,那么这条支路就可以用下 列任何一个元件去替代: (1)电压等于uk的独立电压源; (2)电流等于i k的独立电流源; • 替代后,该电路中其余部分的 电压和电流均保持不变。 (3)阻值等于 的电阻。 uk i k

替代定理的示意图 16 注意极性! Rk N k N us-uk 用电压源替代 注意方向! N R- N ik is-ik 用电阻替代 用电流源替代 2010年3月3日星期三 13
2010年3月3日星期三 13 替代定理的示意图 usk i k N + - Rk + - uk 注意极性! us =u N k + - 用电压源替代 N 用电流源替代 i s =i k 注意方向! N 用电阻替代 R= uk i k

直观地理解 PN ·对给定的一组线性(或非线性)代数方程,只要存在 唯一解,则其中任何一个未知量,如果用解答值去 替代,肯定不会引起其它变量的解答在量值上有所 改变。 ·对电路问题,根据KCL、KVL列出方程,支路电压 和电流是未知量,激励源是已知的。 0 把某支路确定的电压u(或电流i)用数值为u,(或ik) 的理想电压源(或电流源)替代,就相当于把未知量 用其解答值去替代,不会引起任何一个支路电压和 电流发生变化。 2010年3月3日星期三 14
2010年3月3日星期三 14 直观地理解 • 对给定的一组线性(或非线性)代数方程,只要存在 唯一解,则其中任何一个未知量,如果用解答值去 替代,肯定不会引起其它变量的解答在量值上有所 改变。 • 对电路问题,根据KCL、KVL列出方程,支路电压 和电流是未知量,激励源是已知的。 • 把某支路确定的电压uk (或电流i k )用数值为uk (或i k ) 的理想电压源(或电流源)替代,就相当于把未知量 用其解答值去替代,不会引起任何一个支路电压和 电流发生变化
用u,替代时的情况说明 ·替代前后连接相同,故两个电路 Rk k 的KCL和KVL也相同。 Wsk 两个电路的N”相同,故N部分 的支路约束关系也一样。 原电路 在新电路中,k支路被约束,而 电流则可以是任意的。 ● 可见,原电路的所有电压和电流 N 满足新电路的全部约束关系 ·若原电路各支路电压和电流均有 唯一解,则新电路也有,而且原 新电路 电路的解就是新电路的解。 2010年3月3日星期三 15
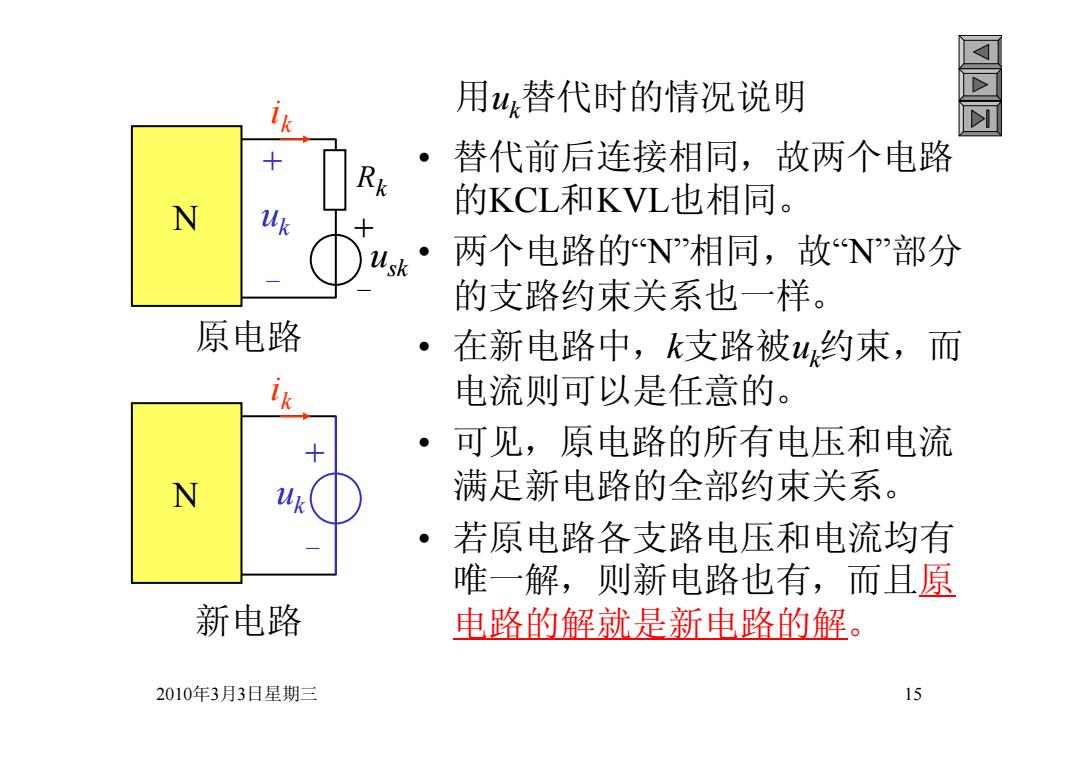
2010年3月3日星期三 15 用uk替代时的情况说明 • 替代前后连接相同,故两个电路 的KCL和KVL也相同。 • 两个电路的“N”相同,故“N”部分 的支路约束关系也一样。 • 在新电路中,k支路被uk约束,而 电流则可以是任意的。 • 可见,原电路的所有电压和电流 满足新电路的全部约束关系。 • 若原电路各支路电压和电流均有 唯一解,则新电路也有,而且原 电路的解就是新电路的解。 usk i k N + - Rk + - uk i k u N k + - 原电路 新电路