模拟滤波器的理想幅频特性 LPAF |H(j2 。π 2 HPAF H() -2c H(2) 2 BPAF BSAF -2c2-2c12c1 2c2 π
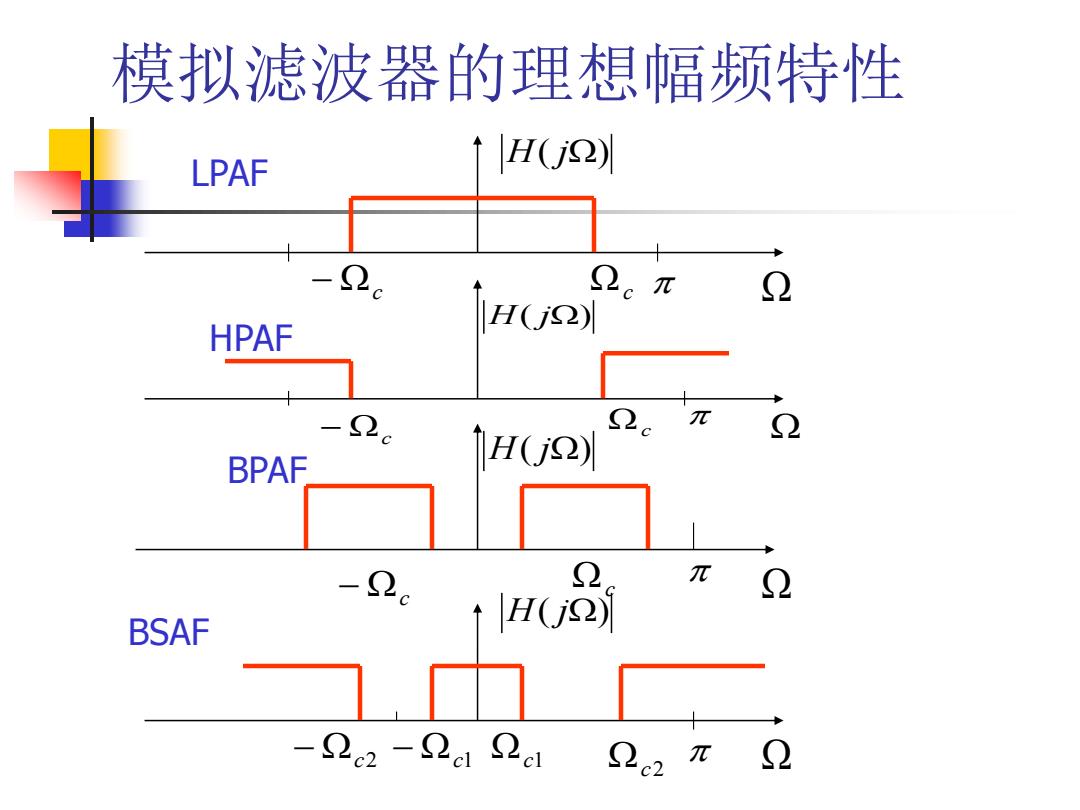
模拟滤波器的理想幅频特性 − c c H( j) LPAF H( j) − c c HPAF H( j) − c c BPAF H( j) − c2 − c1 c1 c2 BSAF
数字滤波器的理想幅频特性 He) 低通 -2元 2元 0 H(ei) 高通 (b) -2m 2元 0 H(e' 带通 (c) 一2元 一元 2π H (ei) 带阻 (d)- 一2元 一元 2π 数字滤波器的珥想幅频特性
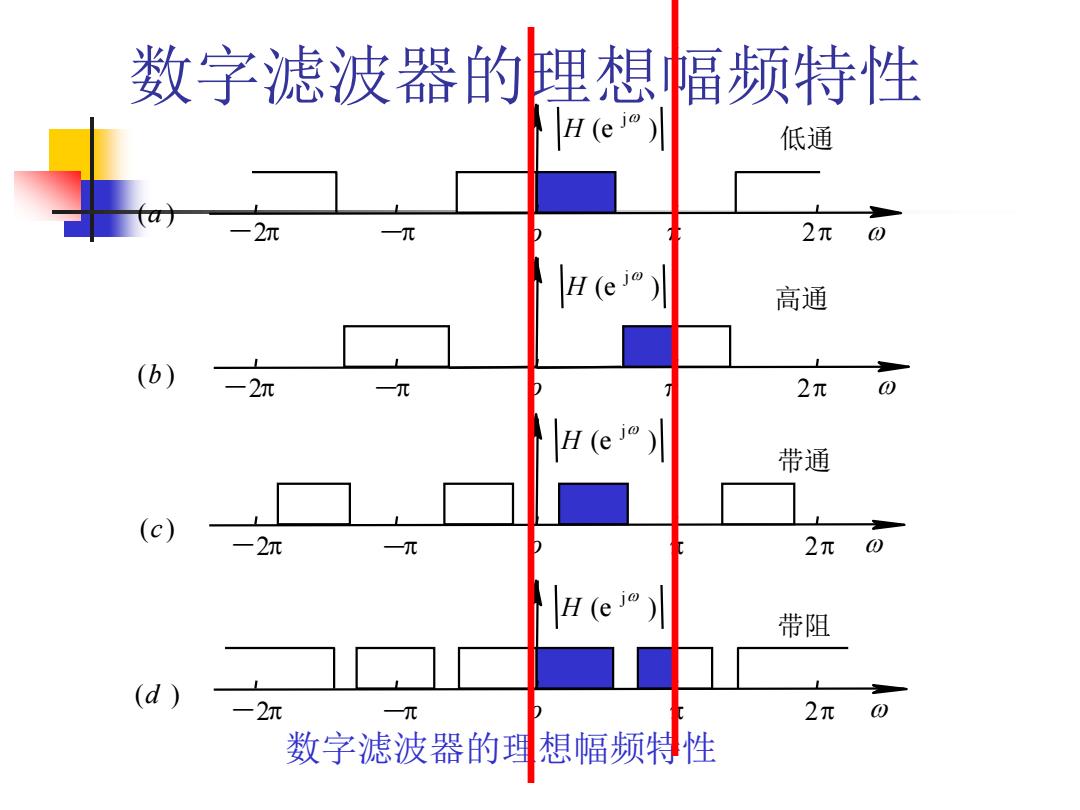
数字滤波器的理想幅频特性 数字滤波器的理想幅频特性 (e ) jw H -2 - o 2 w (e ) jw H -2 - o 2 w (e ) jw H -2 - o 2 w (e ) jw H -2 - o 2 w (a ) (b ) (c ) (d ) 低通 高通 带通 带阻

2)现代滤波器 它主要研究内容是从含有噪声的数据记录(又称 胴间序列)中估计出信号的某些特征或信号本身 一旦信号被估计出,那么估计出的信号将比原信号 会有高的信噪比。 现代滤波器把信号和噪声都视为随机信号,利用 它们的统计特征(如自相关函数、功率谱等)导出 一套最佳估值算法,然后用硬件或软件予以实现。 现代滤波器理论源于维纳在40年代及其以后的工 作,这一类滤波器的代表为:维纳滤波器,此外, 还有卡尔曼滤波器、线性预测器、自适应滤波器。 本课程主要讲经典滤波器
2)现代滤波器 它主要研究内容是从含有噪声的数据记录(又称 时间序列)中估计出信号的某些特征或信号本身。 一旦信号被估计出,那么估计出的信号将比原信号 会有高的信噪比。 现代滤波器把信号和噪声都视为随机信号,利用 它们的统计特征(如自相关函数、功率谱等)导出 一套最佳估值算法,然后用硬件或软件予以实现。 现代滤波器理论源于维纳在40年代及其以后的工 作,这一类滤波器的代表为:维纳滤波器,此外, 还有卡尔曼滤波器、线性预测器、自适应滤波器。 本课程主要讲经典滤波器

3)根据单位脉冲响应()的时宽,即 列长分为: IIR:Infinite impulse Response,即无限长度单 位脉冲响应滤波器 系统函数为:H(z)= i=0 1-∑b,z FIR:Definite impulse Response,即有限长度 单位脉冲响应滤波器 W-1 系统函数为:H(z)=∑h(n)z" n=0
3)根据单位脉冲响应h(n)的时宽,即 列长分为: ◼ IIR:Infinite impulse Response, 即无限长度单 位脉冲响应滤波器 ◼ FIR:Definite impulse Response, 即有限长度 单位脉冲响应滤波器 = − = − − = N i i i M i i i b z a z H z 1 0 1 系统函数为: ( ) − = − = 1 0 ( ) ( ) N n n 系统函数为:H z h n z

4)根据实现的方法分 递归型,IIR一般为递归型 ■非递归型,一般FIR除频率取样设计方法 外
4)根据实现的方法分 ◼ 递归型,IIR一般为递归型 ◼ 非递归型,一般FIR除频率取样设计方法 外