
Xidian University 1.3.1随机过程的基本概念(7〉 若对任给的时刻t和t,如下列函数 Cx(,2)=cov[X(),X(t2)】 (1-5) =E(X(t)-mx()X(t2)-mx(t2)] 存在,则称Cx(t,t2)为X)的协方差函数; 若对任给的时间t,和t2,Rx(t,t2)=E[Xt)Xt2)]存 在,则Rx(t,t)为X0)的自相关函数。 协方差函数,自相关函数、均值函数有下列关系: Cx(t1,t2)=Rx(t1,t2)-mx(t1)mx(t2)(1-7)
1.3.1 随机过程的基本概念(7) 若对任给的时间t 1和t 2, RX(t 1 ,t 2 )=E [X(t 1 ) X(t 2 )]存 在,则 RX(t 1 ,t 2 )为X(t)的自相关函数。 协方差函数,自相关函数、均值函数有下列关系: CX (t 1 ,t 2 ) RX (t 1 ,t 2 ) mX (t 1 )mX (t 2 ) (1-7) 若对任给的时刻t 1和t 2,如下列函数 (1-5) 存在,则称CX(t 1 ,t 2 )为X(t)的协方差函数; ( ( ) ( ))( ( ) ( )) ( , ) cov ( ), ( ) 1 1 2 2 1 2 1 2 E X t m t X t m t C t t X t X t X X X

Xidian University 1.3.1随机过程的基本概念(8) 下面介绍几类典型的随机过程: 1.独立随机过程 2.马尔可夫Markov)过程 3.独立增量过程 4.平稳随机过程 5.Poisson过程 6.马尔可夫链
1.3.1 随机过程的基本概念(8) 下面介绍几类典型的随机过程: 1.独立随机过程 2.马尔可夫(Markov)过程 3.独立增量过程 4.平稳随机过程 5 .Poisson过程 6 .马尔可夫链

Xidian University 1.独立随机过程 设有一个随机过程X),如果对任意给定的时刻t, t2… tn,随机变量Xt,X化2),,Xt)是相互独 立的,也就是其n维分布函数可以表示为: Fh.(x1,x2,,xn)=F,(x) =1 (1-8) 则称X()是独立随机过程。该过程的特点是任意一时 刻的状态与其他任何时刻的状态无关
1.独立随机过程 设有一个随机过程X(t) ,如果对任意给定的时刻t 1, t 2 ,… ,t n ,随机变量X(t 1 ), X(t 2 ),…, X(t n )是相互独 立的,也就是其n维分布函数可以表示为: n i t t t n t i F x x x F x n i 1 , ,..., 1 2 ( , ,..., ) ( ) 1 2 t 1 t 2 t 3 t n-2 t n-1 t n X(t) t (1-8) 则称X(t)是独立随机过程。该过程的特点是任意一时 刻的状态与其他任何时刻的状态无关
Xidian University 2.马尔可夫(Markov)过程(1) 设有X)一个随机过程,如果对于一个任意的时间序 列:t不12<.<1n,n23,在给定随机变量的X)=x1, Xt2)=x2,·,Xn=xm条件下,Xt=xn的分布可 以表示为: En4hn(a出,2…xn-i)=Fa(nxn-) (1-9) 则称X()为马尔可夫过程或简称为马氏过程。 n-
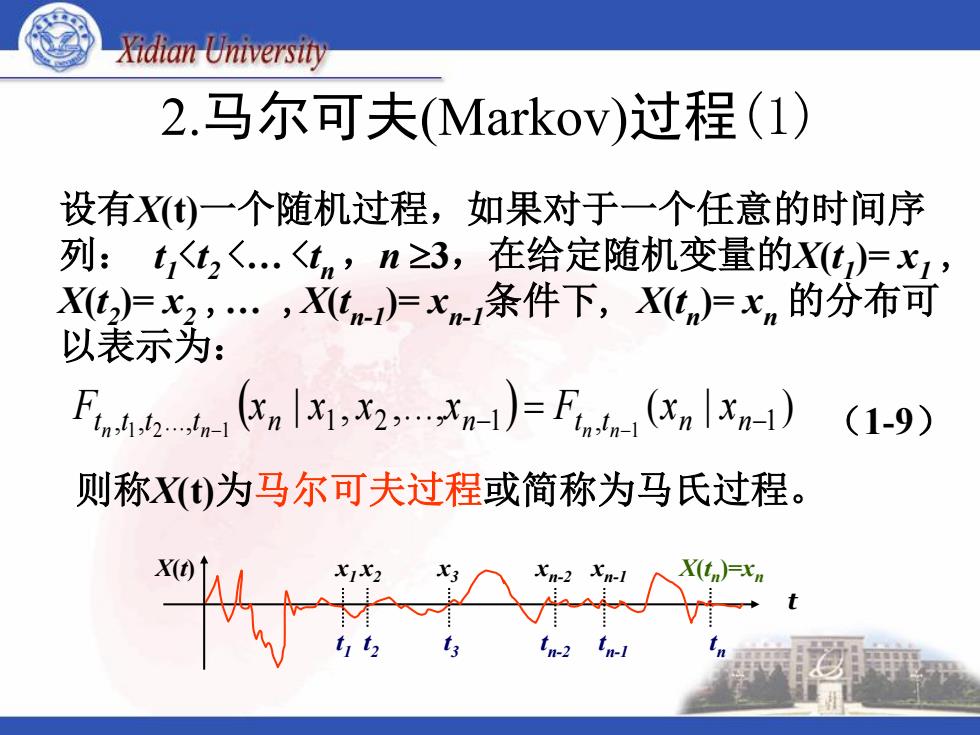
2.马尔可夫(Markov)过程(1) 设有X(t)一个随机过程,如果对于一个任意的时间序 列: t 1 <t 2 <… <t n ,n 3,在给定随机变量的X(t 1 )= x1 , X(t 2 )= x2 ,… ,X(t n-1 )= xn-1条件下, X(t n )= xn 的分布可 以表示为: | , ,..., ( | ) , , ..., 1 2 1 , 1 t t 1 t 2 t 1 n n t t 1 n n F x x x x F x x n n n n t 1 t 2 t 3 t n-2 t n-1 t n X(t) t x1 x2 x3 xn-2 xn-1 X(tn )=xn (1-9) 则称X(t)为马尔可夫过程或简称为马氏过程

Xidian University 2.马尔可夫(Markov)过程(2) 该过程的基本特点是无后效性。即当该过程在时 刻的状态为已知的条件下,则该过程在t(>t)所处的 状态与该过程在t时刻之前的状态无关。 En4hnx,x2,…xn-)=En(xnxn1) 式(1-9)右端的条件分布函数可以写成: F,(x|x)=P{X(t)<x|X(t)=x'}, t>t(1-10) 该式称为马氏过程的转移概率
2.马尔可夫(Markov)过程(2) 该过程的基本特点是无后效性。即当该过程在t 0时 刻的状态为已知的条件下,则该过程在t (>t0 )所处的 状态与该过程在t 0时刻之前的状态无关。 式(1-9)右端的条件分布函数可以写成: (1-10) 该式称为马氏过程的转移概率。 ( | ') { ( ) | ( ') '}, ' , ' F x x P X t x X t x t t t t | , ,..., ( | ) , , ..., 1 2 1 , 1 t t 1 t 2 t 1 n n t t 1 n n F x x x x F x x n n n n