
Xidian University 3.独立增量过程 设Xt)Xt)=Xt1,t)是随机过程X)在时间间隔[t1,) 上的增量,如果对于时间t的任意n个值0≤tt,<.<tn 增量X1,),X23,,Xn-1,)是相互独立的,则称 X()为独立增量过程。 X612)X62,43) X(tn-2tn-1)X(tn-itn) (t X1)X2)X) X(tn2)X(tn-i X(t) 该过程的特点是:在任一时间间隔上,随机过程状态 的改变并不影响未来任一时间间隔上状态的改变。可 以证明独立增量过程是一种特殊的马尔可夫过程
3.独立增量过程 设X(t 2 )- X(t 1 )= X(t 1 ,t 2 )是随机过程X(t)在时间间隔[t 1 ,t 2 ) 上的增量,如果对于时间t的任意n个值0t 1 <t 2 <…<t n , 增量X(t 1 ,t 2 ), X(t 2 ,t 3 ),…, X(t n-1 ,t n )是相互独立的,则称 X(t)为独立增量过程。 该过程的特点是:在任一时间间隔上,随机过程状态 的改变并不影响未来任一时间间隔上状态的改变。可 以证明独立增量过程是一种特殊的马尔可夫过程。 t 1 t 2 t 3 t n-2 t n-1 t n X(t) t X(t1 ) X(t2 ) X(t3 ) X(tn-2 ) X(tn-1 ) X(tn ) X(t1 ,t2 ) X(t2 ,t3 ) X(tn-2 ,tn-1 ) X(tn-1 ,tn )
Xidian University 4. 平稳随机过程(1) 如果对于时间t的任意个值t1,t2,.,tn和任意实数6, 随机过程X()的n维分布函数满足关系式: Eh,,(1,2…n)=E+8h+e,…hte(1,x2…Xn)(1-11) 则称X)为平稳随机过程或简称为平稳过程。 十8 t,+8 按照上述定义的随机过程通常称为严(狭义)平稳过程。 该过程的特点是随机过程的统计特性不随时间的平移而 变化
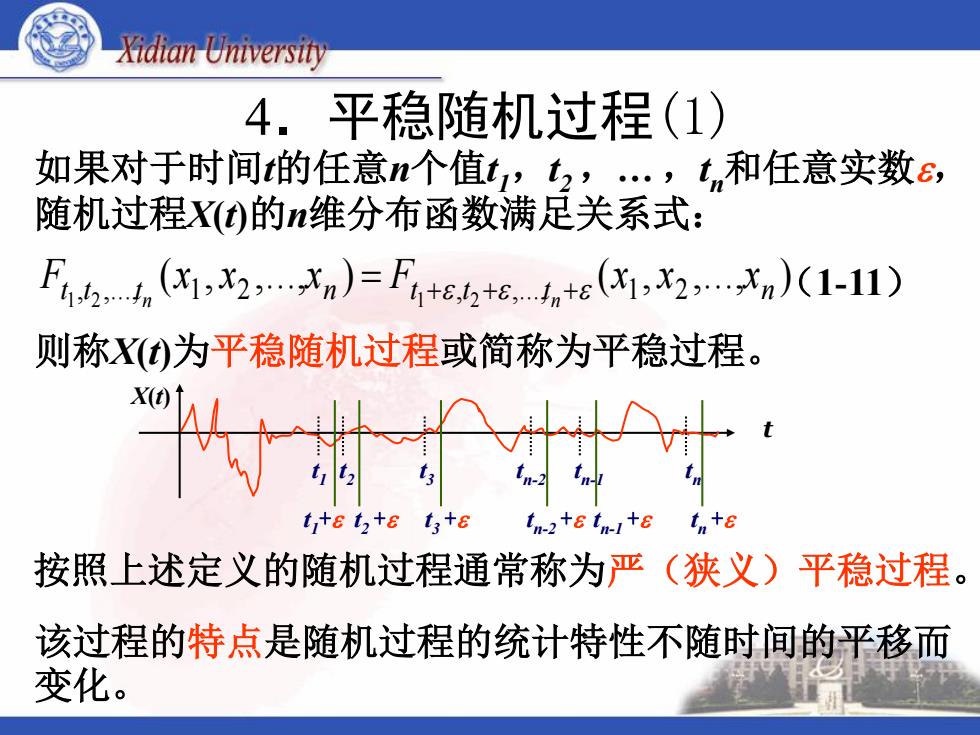
4.平稳随机过程(1) 如果对于时间t的任意n个值t 1,t 2 ,… ,t n和任意实数, 随机过程X(t)的n维分布函数满足关系式: (1-11) 则称X(t)为平稳随机过程或简称为平稳过程。 ( , ,..., ) ( , ,..., ) , ,..., 1 2 , ,..., 1 2 1 2 1 2 t t t n t t t n F x x x F x x x n n 该过程的特点是随机过程的统计特性不随时间的平移而 变化。 t 1 t 2 t 3 t n-2 t n-1 t n X(t) t t 1 + t 2 + t 3 + t n-2 + t n-1 + t n + 按照上述定义的随机过程通常称为严(狭义)平稳过程

Xidian University 4.平稳随机过程(2) 在实际应用中,我们更关心这样一类过程:其 EX()]<o(称为二阶矩过程),且满足下列条件: 1)均值为常量(与时间t无关); 2)对于任意时刻s和t,其相关函数满足Rxs,)=Rxt-s), 即相关函数仅与时差t-s有关,而与3,的取值无关; 称这类过程为宽(广义)平稳过程。在实际应用中所指 的随机过程通常是宽平稳过程
4.平稳随机过程(2) [ ( ) ] 2 E X t 在实际应用中,我们更关心这样一类过程:其 (称为二阶矩过程),且满足下列条件: 1)均值为常量(与时间t无关); R (s,t) R (t s) X X 2)对于任意时刻s和t,其相关函数满足 , 即相关函数仅与时差t-s有关,而与s,t的取值无关; 称这类过程为宽(广义)平稳过程。在实际应用中所指 的随机过程通常是宽平稳过程

Xidian University 4. 平稳随机过程(3) •当一个严平稳过程的一阶矩、二阶矩存在时,它 一定是宽平稳过程;否则,结论不成立。 ·一般的宽平稳过程不是严平稳过程,因为“一阶矩 与时间无关”是不能推出它的概率分布也与时间无 关;同样,自相关函数只依赖于时间差,也不能 推出它的二维联合概率分布与采样时间有关。 如果一个过程的所有的高阶矩或高阶相关函数完 全由一阶矩、二阶矩决定,此时,宽平稳与严平 稳是等价的。到目前为止,我们了解到的具有此 类特征的过程只有正态过程(高斯过程)
4.平稳随机过程(3) •当一个严平稳过程的一阶矩、二阶矩存在时,它 一定是宽平稳过程;否则,结论不成立。 •一般的宽平稳过程不是严平稳过程,因为“一阶矩 与时间无关”是不能推出它的概率分布也与时间无 关;同样,自相关函数只依赖于时间差,也不能 推出它的二维联合概率分布与采样时间有关。 •如果一个过程的所有的高阶矩或高阶相关函数完 全由一阶矩、二阶矩决定,此时,宽平稳与严平 稳是等价的。到目前为止,我们了解到的具有此 类特征的过程只有正态过程(高斯过程)
Xidian University 各态历经性(1) 各态历经性研究如何从过程的一次观察记录确定 其各种统计量的问题。 为了说明各态历经性,在时间轴上定义下列两种平均: (M X(t)>=lim (1-12) 飞X0)Xt+z)=m2元XOXt+x)a边 ,(1-13) 为随机过程的时间均值和时间相关函数
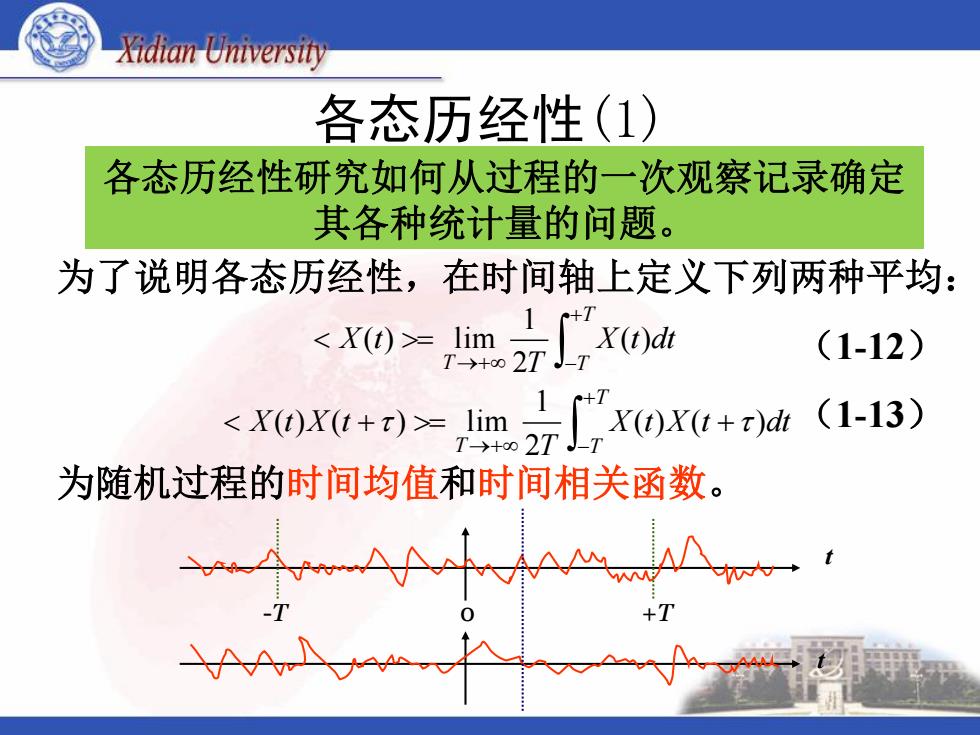
各态历经性(1) 为了说明各态历经性,在时间轴上定义下列两种平均: (1-12) (1-13) 为随机过程的时间均值和时间相关函数。 T T T X t dt T X t ( ) 2 1 ( ) lim T T T X t X t dt T X t X t ( ) ( ) 2 1 ( ) ( ) lim -T 0 +T t t 各态历经性研究如何从过程的一次观察记录确定 其各种统计量的问题