
Xidian University 1.3通信网络中的数学基础 口1.3.1随机过程的基本概念 口1.3.2 Poiss0n过程 口1.3.3马尔可夫链
1.3 通信网络中的数学基础 1.3.1 随机过程的基本概念 1.3.2 Poisson过程 1.3.3 马尔可夫链
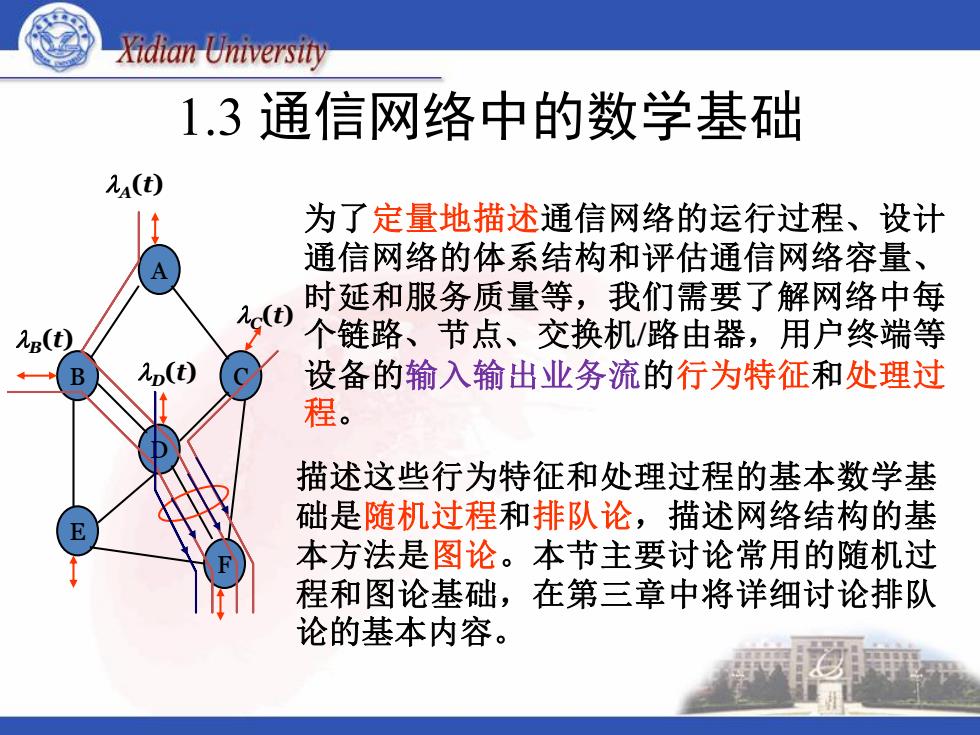
Xidian University 1.3通信网络中的数学基础 2a(t) 为了定量地描述通信网络的运行过程、设计 通信网络的体系结构和评估通信网络容量、 时延和服务质量等,我们需要了解网络中每 Ac(t) Ag(t) 个链路、节点、交换机/路由器,用户终端等 B Ap(t) 设备的输入输出业务流的行为特征和处理过 程。 描述这些行为特征和处理过程的基本数学基 础是随机过程和排队论,描述网络结构的基 E 本方法是图论。本节主要讨论常用的随机过 程和图论基础,在第三章中将详细讨论排队 论的基本内容
1.3 通信网络中的数学基础 为了定量地描述通信网络的运行过程、设计 通信网络的体系结构和评估通信网络容量、 时延和服务质量等,我们需要了解网络中每 个链路、节点、交换机/路由器,用户终端等 设备的输入输出业务流的行为特征和处理过 程。 A E F D B C A(t) C (t) D(t) B(t) 描述这些行为特征和处理过程的基本数学基 础是随机过程和排队论,描述网络结构的基 本方法是图论。本节主要讨论常用的随机过 程和图论基础,在第三章中将详细讨论排队 论的基本内容
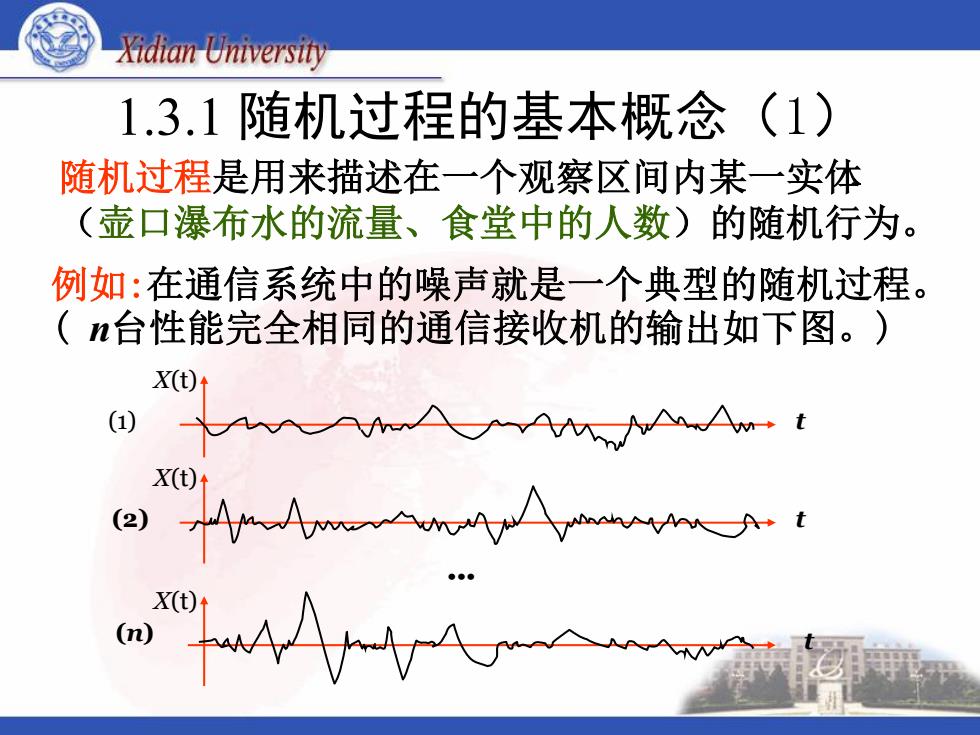
Xidian University 1.3.1随机过程的基本概念(1) 随机过程是用来描述在一个观察区间内某一实体 (壶口瀑布水的流量、食堂中的人数)的随机行为。 例如:在通信系统中的噪声就是一个典型的随机过程。 (n台性能完全相同的通信接收机的输出如下图。) X(t) AAvAAaAwmt X(t) (2) X()
1.3.1 随机过程的基本概念(1) 随机过程是用来描述在一个观察区间内某一实体 (壶口瀑布水的流量、食堂中的人数)的随机行为。 t t t X(t) X(t) X(t) (1) (2) (n) ••• 例如:在通信系统中的噪声就是一个典型的随机过程。 ( n台性能完全相同的通信接收机的输出如下图。)
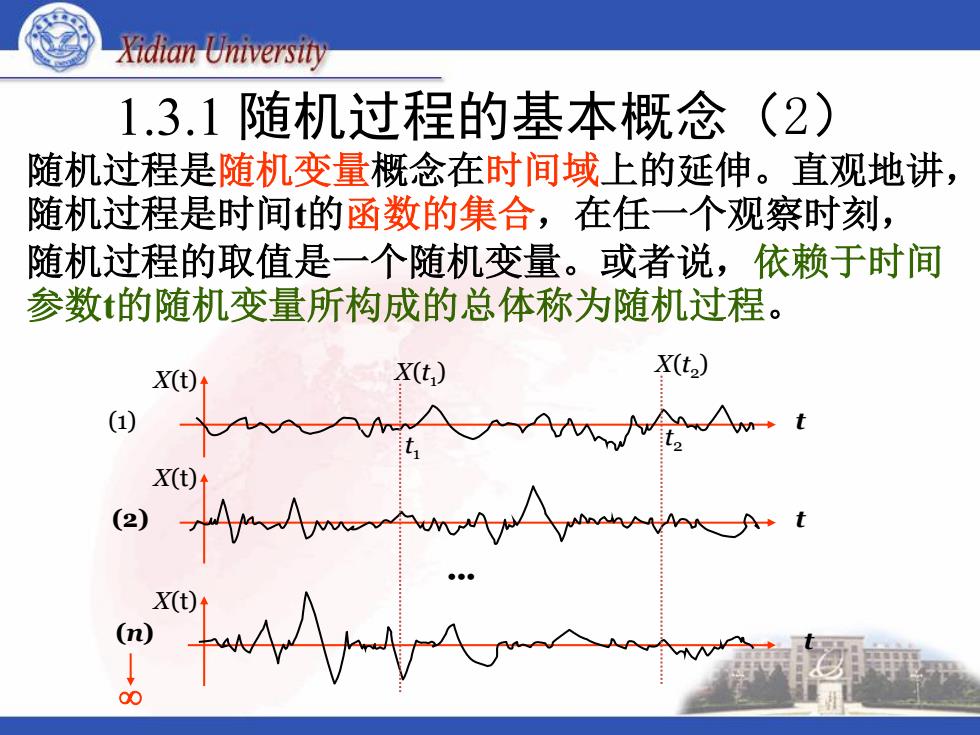
Xidian University 1.3.1随机过程的基本概念(2) 随机过程是随机变量概念在时间域上的延伸。直观地讲, 随机过程是时间的函数的集合,在任一个观察时刻, 随机过程的取值是一个随机变量。或者说,依赖于时间 参数的随机变量所构成的总体称为随机过程。 X(t,) X(t2) 1 X(t) (2) X() (n)
1.3.1 随机过程的基本概念(2) 随机过程是随机变量概念在时间域上的延伸。直观地讲, 随机过程是时间t的函数的集合,在任一个观察时刻, 随机过程的取值是一个随机变量。或者说,依赖于时间 参数t的随机变量所构成的总体称为随机过程。 t t t X(t) X(t) X(t) (1) (2) (n) ••• t1 X(t1 ) t2 X(t2 )

Xidian University 什么是随机变量? 随机变量:某一变量以一定的概率取一确定的值, 通常将这种变量称为随机变量。 随机变量:定义在样本空间上的一个实值函数, 或者说是样本空间到实数的一个映射。 1 if w=heads Y(w)= 0 ifw=tails】
什么是随机变量? 随机变量:某一变量以一定的概率取一确定的值, 通常将这种变量称为随机变量。 随机变量:定义在样本空间上的一个实值函数, 或者说是样本空间到实数的一个映射