
例:求系统r"(t)+3r'(t)2r)=(的系统函数 令e(t)=eor设r(t)=Ae 2r(t)=2Aeior 3r'(t)=3A(j@)eio 可求出A + r"(t)=A(jo)2ejor A[(j@)2+3(j@)+2]el@=eio ejm r(t)= (jo)2+3(jo)+2 H(jo)-20 (U0)2+3j0)+2
16 例:求系统 ( ) 3 ( ) 2 ( ) ( ) " ' r t + r t + r t = e t j t j t j t r t A j e r t A j e r t Ae 2 " ( ) ( ) 3 '( ) 3 ( ) 2 ( ) 2 === j t j t A j j e e [( ) + 3 ( ) + 2 ] = 2 ( ) 3 ( ) 2 ( ) 2 + + = j j e r t j t ( ) 3 ( ) 2 ( ) 1 ( ) 2 + + = = e j j r t H j j t 可求出 A 的系统函数 j t e t e 令 ( ) = j t r t Ae 设 ( ) =
4、当已知具体电路的情况下,系统函数可以由 电路的零状态响应频域等效电路模型来求取,而无 需列写电路的微分方程。 1 R←→R L←→ioL C←> joC 例:求图示电路的系统函数H(j®) 10 y() T
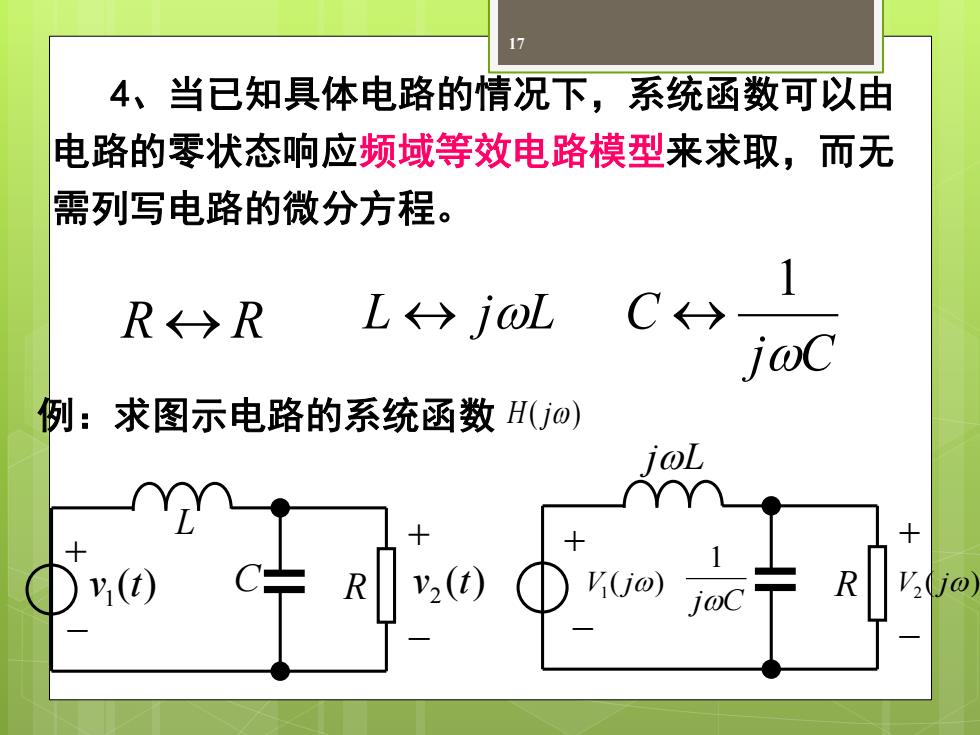
17 4、当已知具体电路的情况下,系统函数可以由 电路的零状态响应频域等效电路模型来求取,而无 需列写电路的微分方程。 R R L jL j C C 1 例:求图示电路的系统函数 H ( j) L + − ( ) 1 v t ( ) 2 v t + − C R + − + − ( ) V1 ( j) V2 j jL jC 1 R
解:由频域等效模型得: V(j@) joC R V(jo) 1 +j@C (j0)= R '(j)= L V(jo) joL+ +j@C (jo)LC+joR R .H(jω)= '(jo) V(j@) (oIC+jo
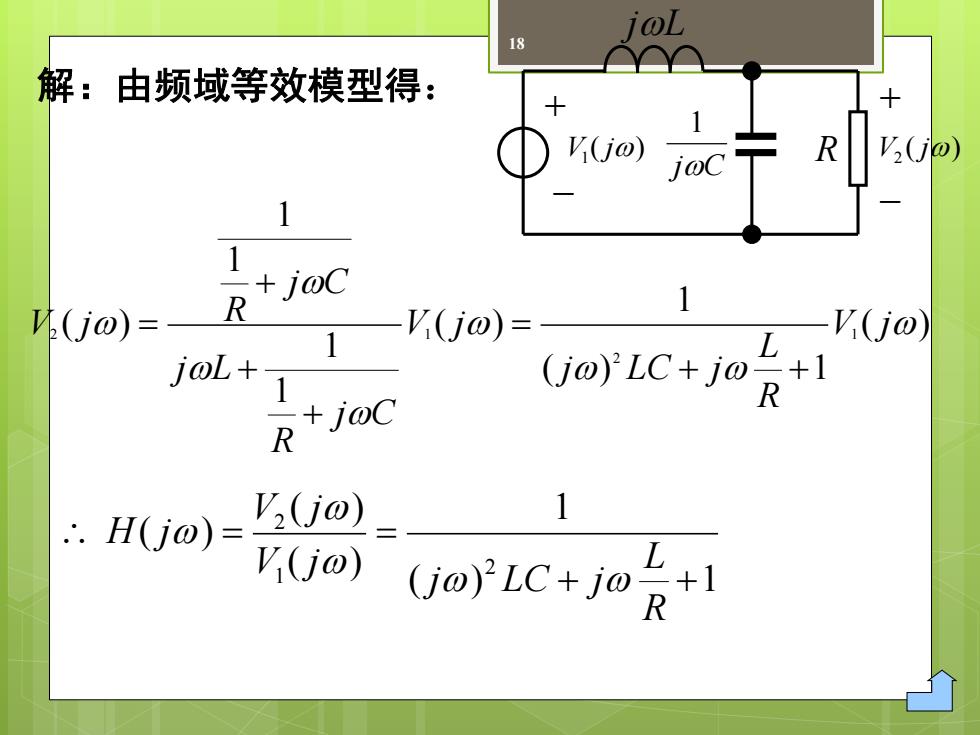
18 解:由频域等效模型得: ( ) ( ) 1 1 ( ) 1 1 1 1 ( ) 1 2 2 1 V j R L j LC j V j j C R j L j C R V j + + = + + + = + − + − ( ) V1 ( j) V2 j jL jC 1 R ( ) 1 1 ( ) ( ) ( ) 2 1 2 + + = = R L j LC j V j V j H j

19 二、系统的频域分析 又称傅立叶变换分析法,频域分析的一般步骤: 1、 求取激励信号的傅立叶变换,即:e①←→E(jo) 2、 确定系统的系统函数H(jo) 3、 求取响应的傅立叶变换RGo)=H(jo)E(jo) 4、将RGo)从频域反变换到时域,从而得到零状态 响应的时域表示式r()
19 又称傅立叶变换分析法,频域分析的一般步骤: 1、求取激励信号的傅立叶变换,即: 2、确定系统的系统函数 3、求取响应的傅立叶变换 4、将 从频域反变换到时域,从而得到零状态 响应的时域表示式 。 R(j) = H(j)E(j) H(j) R(j) 二、系统的频域分析 e(t) E(j) r(t)

例:已知系统的传递函数o)=,。,输入激励为 j0+2 x(t)=(t),试求系统的零状态响应 解:X(Uo)=x@)t1 jo Y(j@)=H(j@)X(j@) Y(j0)=-1 wr+ j0+2 j0(0+2) y0=号1-e"(④
20 试求系统的零状态响应 例:已知系统的传递函数 输入激励为 ( ) ( ), , 2 1 ( ) x t u t j H j = + = j X j 1 解: ( ) = ( ) + Y ( j) = H ( j)X ( j) ( 2) 1 ( ) 2 1 ] 1 [ ( ) 2 1 ( ) + + + + = + = j j j j j Y j 2 2 1 2 1 ( ) 2 + = + − j j 2 2 1 ] 1 [ ( ) 2 1 + = + − j j (1 ) ( ) 2 1 ( ) 2 y t e u t − t = −