
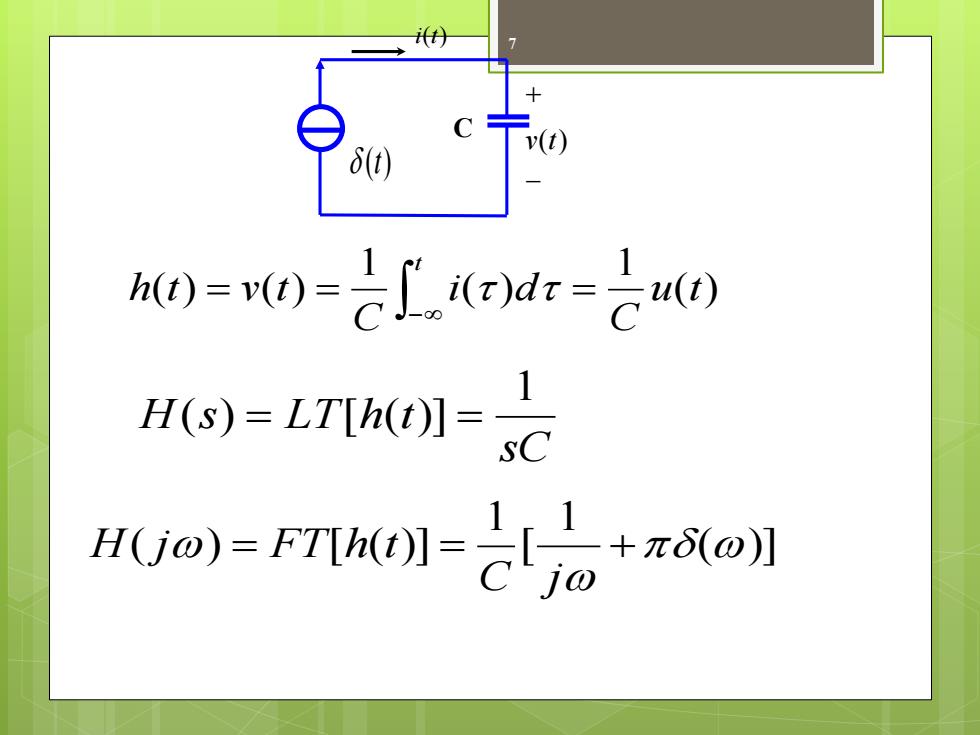
H(Go)称为系统傅立叶变换形式的系统函数, 又称频率响应。 1、H(Go)与H(s)的关系 对于稳定的因果系统,将H(s)中的s代之以jo即可 得到(jo) 如图所示电容模型,输入为电流源 电流,输出为电容两端电压,求冲激 响应h(t)人系统函数H(s)、H(jo)
6 称为系统傅立叶变换形式的系统函数, 又称频率响应。 H(j) 1、 H(j) 与 H(s) 的关系 对于稳定的因果系统,将 中的s代之以 即可 得到 H(j) 。 H(s) j 如图所示电容模型,输入为电流源 电流,输出为电容两端电压,求冲激 响应 h(t) 、系统函数 H(s) 、 H( j) 。 (t) - + v(t) C
hMo)=0=己(r)ar=己0 1h刃=C HUo)=rIel-之1a+ao】
7 ( ) 1 ( ) 1 ( ) ( ) u t C i d C h t v t t = = = − ( )] 1 [ 1 ( ) [ ( )] = = + C j H j FT h t sC H s LT h t 1 ( ) = [ ( )] = (t) − + v(t) C i(t)

2、 由R(jo)=(jo)H(jo)得到的RGo是系统的零状态响应。 3、H(jo)函数的物理意义 E(jo R(j0)=E(jo)Hjo) H(j@) 如果激励信号的频谱密度函数为E(jo),则响应的 频谱密度函数便是H(Uo)E(jo),系统改变了激励信号 的频谱。系统的功能是对信号个频率分量进行加权, 某些频率分量增强,而另一些频率分量则相对削弱或 不便
8 3、 H( j) 函数的物理意义 如果激励信号的频谱密度函数为 ,则响应的 频谱密度函数便是 ,系统改变了激励信号 的频谱。系统的功能是对信号个频率分量进行加权, 某些频率分量增强,而另一些频率分量则相对削弱或 不便。 E( j) H( j)E( j) 2、由 R( j) = E( j)H( j) 得到的 R(jω) 是系统的零状态响应。 E( j) R( j) = E( j)H( j) H( j)

5.2利用系统函数(jo)求响应 一、 系统函数的求取方法 二、系统的频域分析 三、关于频域分析的说明 四、周期信号通过线性系统
9 四、周期信号通过线性系统 5.2 利用系统函数 H(j) 求响应 一、系统函数的求取方法 二、系统的频域分析 三、关于频域分析的说明

一、系统函数的求取方法 >利用微分方程 >利用冲激响应 >通过特定激励下的零状态响应 >通过电路的零状态响应频域等效电路模型
10 一、系统函数的求取方法 ➢利用微分方程 ➢利用冲激响应 ➢通过特定激励下的零状态响应 ➢通过电路的零状态响应频域等效电路模型