
■(1)自由度和平方和的分解 ■①自由度的分解: ■总 DFx=nk-1=(3×8)-1=23 ■区组 DFR=n-1=3-1=2 ■品种 DF,=k-1=8-1=7 ·误差 DF=(n-1)(k-1)=(3-1)×(8-1)=14 ■②平方和的分解: ■矫正数 C=T2 278.02 =3220.17 nk3×8
◼ (1) 自由度和平方和的分解 ◼ ① 自由度的分解: ◼ 总 ◼ 区组 ◼ 品种 ◼ 误差 ◼ ② 平方和的分解: ◼ 矫正数 DFT = nk − 1 =(3 8)− 1 = 23 DFR = n − 1 = 3 − 1 = 2 DFt = k −1 = 8 −1 = 7 DFe =(n − 1)(k − 1)=(3 − 1)(8 − 1)= 14 3220.17 3 8 278.02 = = = nk T C 2
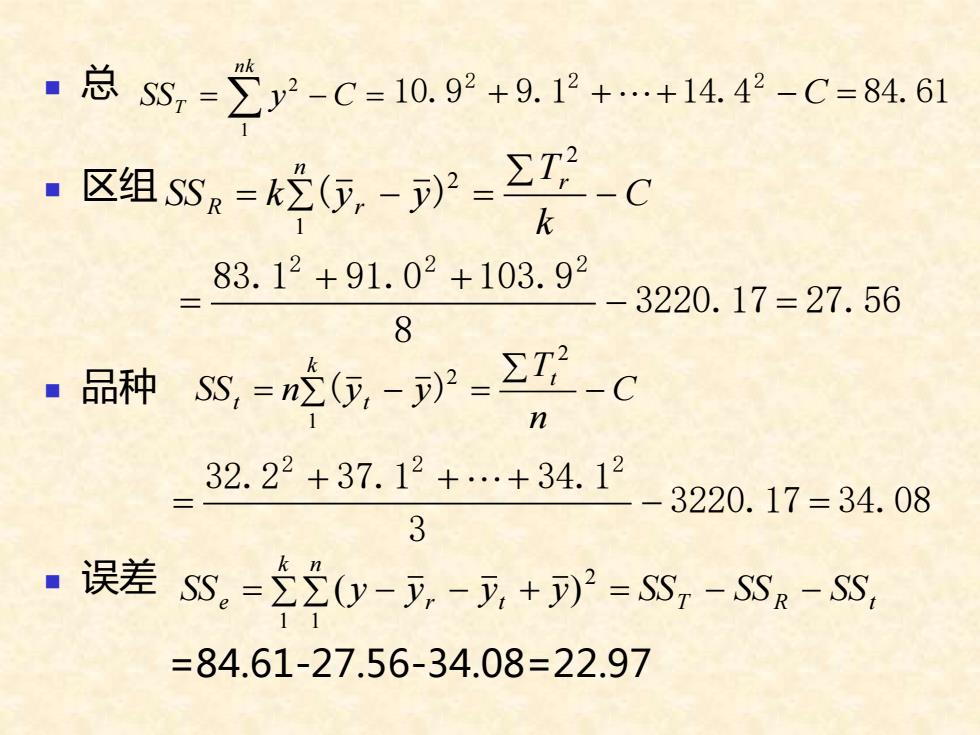
·总5S,-2y2-C=10.92+9.12++14.42-C=84.61 ·区组sS=k,-)-C k 83.12+91.02+103.9 -3220.17=27.56 8 ■品 中58,=吃,-y-7-C n 32.22+37.12++34.1-3220.17=34.08 3 ■误差 SS。=220y-元-元,+5)2=SSr-SSR-SS, =84.61-27.56-34.08=22.97
◼ 总 ◼ 区组 ◼ 品种 ◼ 误差 =84.61-27.56-34.08=22.97 = − = nk SST y C 1 2 10.9 9.1 14.4 84.61 2 2 2 + ++ − C = − = − = n r R r C k T SS k y y 1 2 2 ( ) 3220.17 27.56 8 83.1 91.0 103.9 2 2 2 − = + + = − = − = k t t t C n T SS n y y 1 2 2 ( ) 3220.17 34.08 3 32.2 37.1 34.1 2 2 2 − = + + + = T R t k n SSe = y − yr − yt + y = SS − SS − SS 1 1 2 ( )
■(2)F测验 将上述计算结果列入表12.4,算得各变异来源的MS值。 表12.4表12.3结果的方差分析 变异来源 DF SS MS F F0.05 区组间 2 27.56 13.78 8.40 3.74 品种间 7 34.08 4.87 2.97 2.77 误差 14 22.97 1.64 总变异 23 84.61
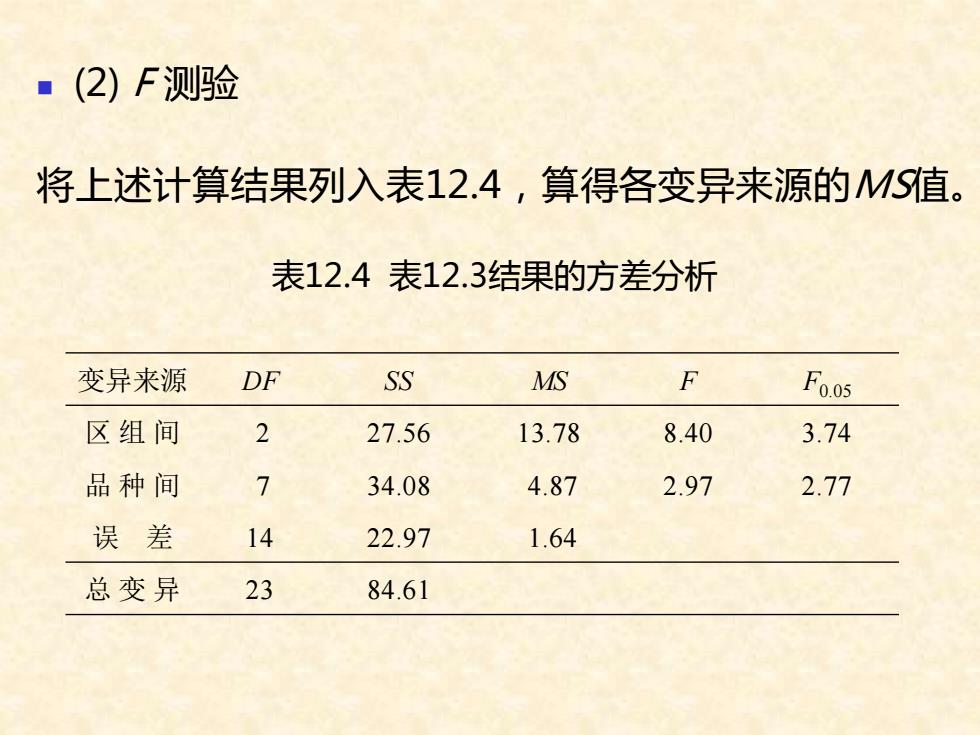
◼ (2) F 测验 将上述计算结果列入表12.4,算得各变异来源的MS值。 表12.4 表12.3结果的方差分析 变异来源 DF SS MS F F0.05 区 组 间 2 27.56 13.78 8.40 3.74 品 种 间 7 34.08 4.87 2.97 2.77 误 差 14 22.97 1.64 总 变 异 23 84.61

对区组间MS作F测验,在此有H4,=山2=43 HA山、4④全相等(、41、分别优表区组I、 Ⅱ、Ⅲ的总体平均数), ■得F=13.78/1.64=8.40>F.05,所以H6应予否定 说明3个区组间的土壤肥力有显著差别。在这个试验 中,区组作为局部控制的一项手段,对于减少误差是 相当有效的(一般区组间的测验可以不必进行,因为 试验目的不是研究区组效应)
◼ 对区组间MS作F测验,在此有H0: , HA: 、 、 不全相等( 、 、 分别代表区组Ⅰ、 Ⅱ、Ⅲ的总体平均数), ◼ 得F =13.78/1.64=8.40>F0.05,所以H0应予否定, 说明3个区组间的土壤肥力有显著差别。在这个试验 中,区组作为局部控制的一项手段,对于减少误差是 相当有效的(一般区组间的F测验可以不必进行,因为 试验目的不是研究区组效应)。 1 = 2 = 3 1 2 3 2 3 1

■对品种间MS作F测验,有H64A=4B=.=4H, HA4A、4B、不全相等(、A8 份别代表品种A、B、.、H的总体平均数),得 F=4.87/1.64=2.97>F0.05,所以H6应予否定,说明8 个供试品种的总体平均数有显著差异。需进一步作 多重比较。 ■(3)品种间平均数的多重比较 ■①最小显著差数法(LSD法)本例目的是要测验各供 试品种是否与标准品种A有显著差异,宜应用LSD
◼ 对品种间MS 作F 测验,有H0: , HA: 、 、.、 不全相等( 、 、.、 分别代表品种A、B、.、H的总体平均数),得 F =4.87/1.64=2.97>F0.05,所以H0应予否定,说明8 个供试品种的总体平均数有显著差异。需进一步作 多重比较。 ◼ (3) 品种间平均数的多重比较 ◼ ① 最小显著差数法(LSD法) 本例目的是要测验各供 试品种是否与标准品种A有显著差异,宜应用LSD A = B == H A B H A B H