
注意利用函数的对称性可使系数的确定简化 ①偶函数 i() f0=f八-0 b=0 T/2 ②奇函数 f(t)=-f(t) a2=0 -T2 ③奇谐波函数 f0=-f+) 2k T 返回 上页 下页
利用函数的对称性可使系数的确定简化 ①偶函数 ( ) ( ) 0 k f t f t b ( ) ( ) 0 k f t f t a ②奇函数 ③奇谐波函数 ) 0 2 ( ) ( a2k b2k T f t f t 注意 -T/2 T/2 t f (t) o -T/2 T/2t f (t) o t f (t) o T/2 T 返 回 上 页 下 页
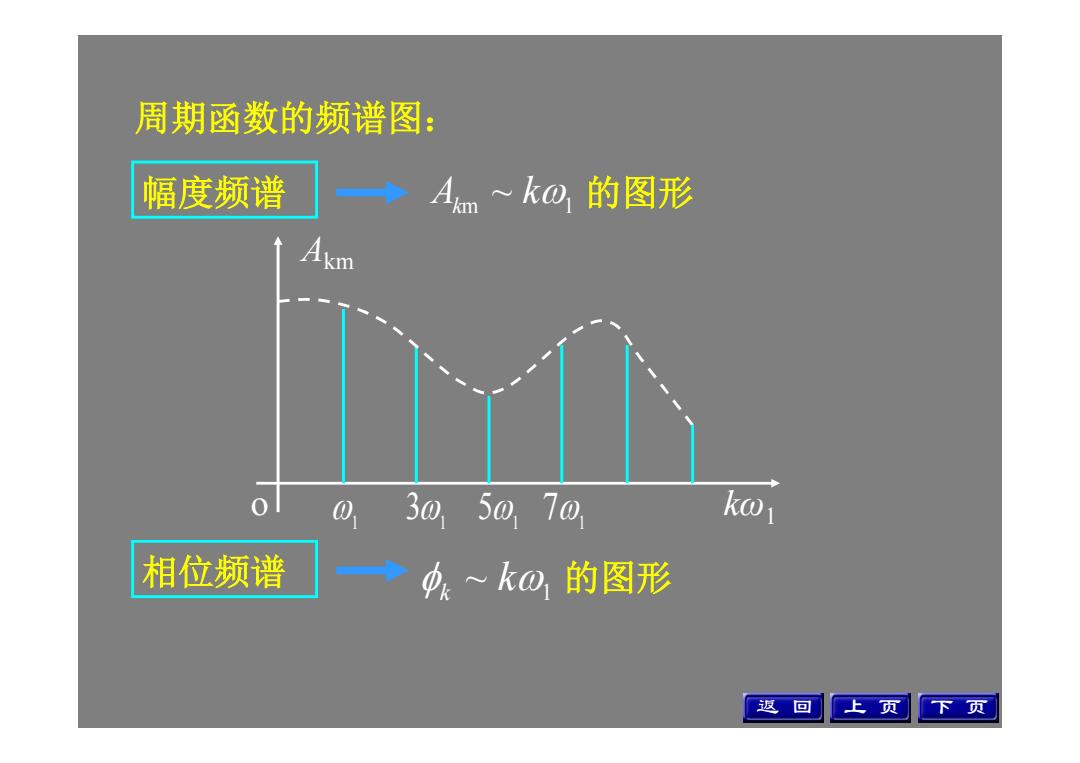
周期函数的频谱图: 幅度频谱 →Am~k0,的图形 01 0 305070 k01 相位频谱 —◆中~k0的图形 返回 上页 下页
周期函数的频谱图: 幅度频谱 A k km 1 ~ 的图形 1 1 1 1 3 5 7 Akm o kω1 相位频谱 k ~ k 1 的图形 返 回 上 页 下 页

例1周期性方波信号的分解 T 0<t< ,(t0= 2 2 T2 T 解 图示矩形波电流在一个周期内的表达式为: 直流分1=.0)d-1.d= 谐波分量: :b=i,(or)sin kord(o0 0 K为偶数 K为奇数 返回 上页 下页
例1 周期性方波信号的分解 解 图示矩形波电流在一个周期内的表达式为: t T T T I t i t S 2 0 2 0 ( ) m 2 d 1 ( )d 1 0 / 2 0 m T T O S m I I t T i t t T 直流分量:I 谐波分量: 2π 0 ( )sin d( ) π 1 b i t k t t K S K为偶数 K为奇数 π 2 0 cos ) 1 ( π π 0 k k t I k I m m t T/2 T S i m I o 返 回 上 页 下 页

2i,(o0)coskd(or)) 21m.Isin kot= kπ (为奇数) 乙的展开式为: 2 2Lemt+sn30r+与sn50r+-) 3 返回 上页 下页
sin 0 1 π 2 ( )cos d( ) π 2 π 0 2π 0 k t k I a i t k t t m k S π 2 2 k 2 k k k I A b a b m K (k为奇数) s i 的展开式为: sin 5 ) 5 1 sin 3 3 1 (sin π 2 2 t t t I I i m m S 返 回 上 页 下 页
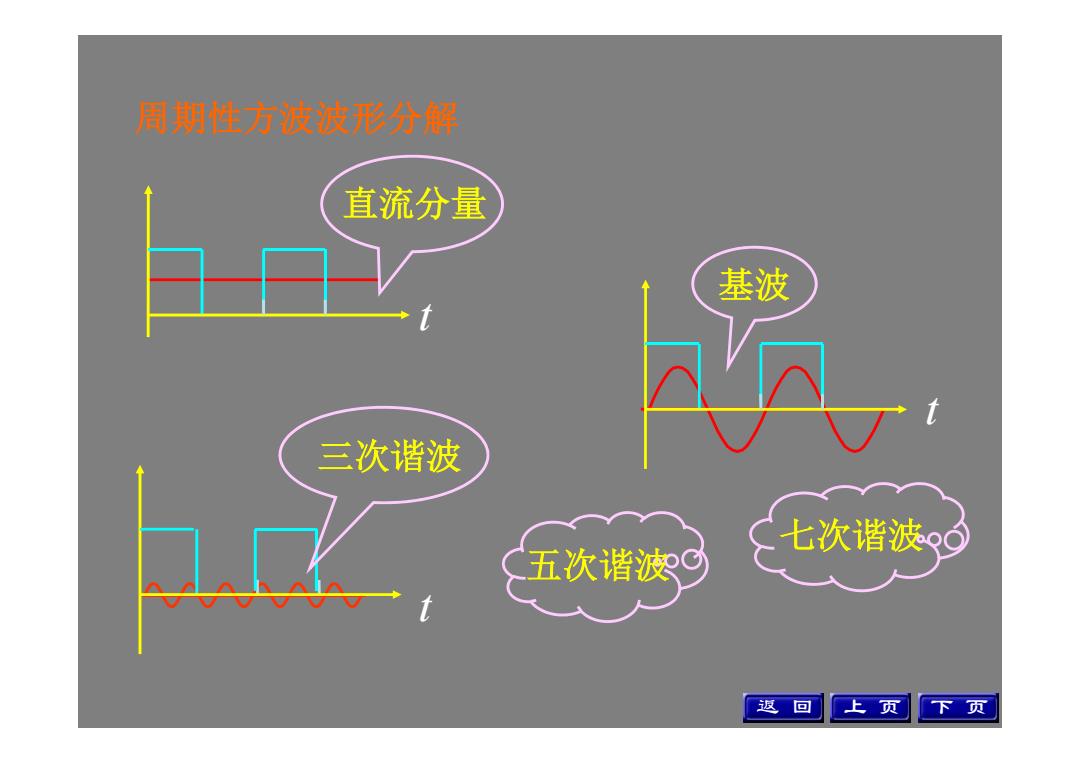
周期性方波波形分解 直流分量 基波 三次谐波 七次谐波 五次谐波G A 返回 上页 下页
t t t 基波 直流分量 三次谐波 五次谐波 七次谐波 周期性方波波形分解 返 回 上 页 下 页