河南大学：《电路原理》课程电子教案（课件讲稿）第13章 非正弦周期电流电路和信号的频谱

例4交直流共存电路 A ①AA 返回 上页 下页

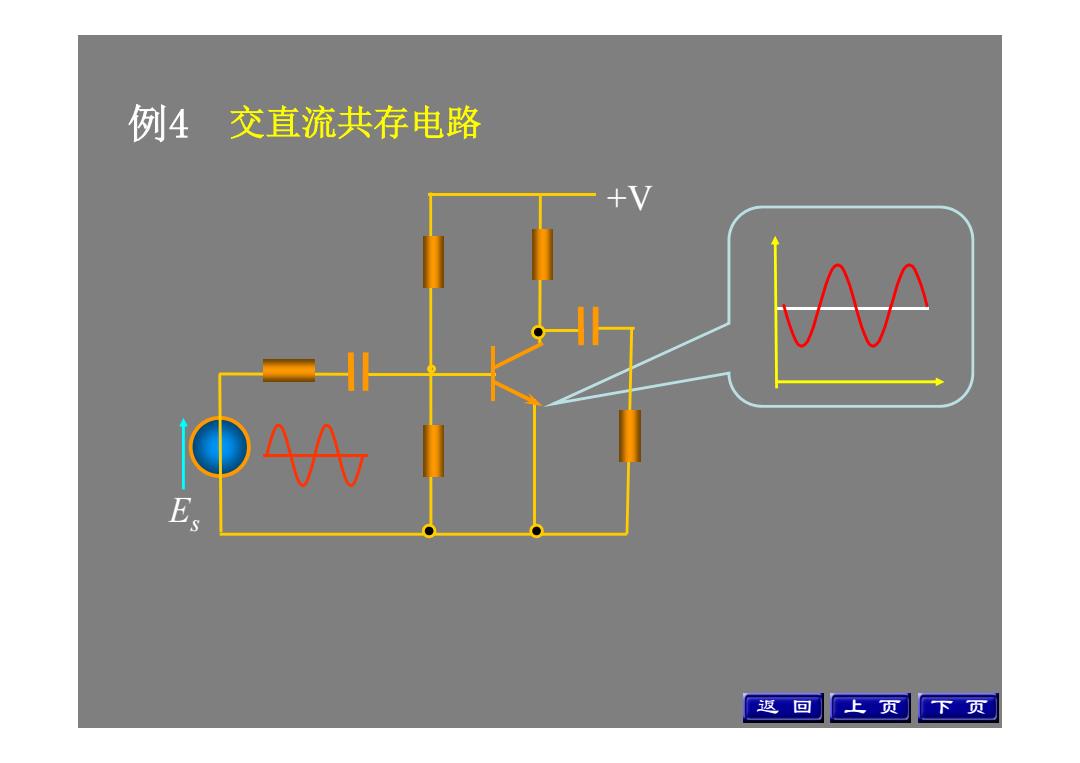
例4 交直流共存电路 +V Es 返 回 上 页 下 页

13.2周期函数分解为傅里叶级数 若周期函数满足狄利赫利条件： ①周期函数极值点的数目为有限个： ②间断点的数目为有限个； ③在一个周期内绝对可积，即： [f(t)dt 0 可展开成收敛的傅里叶级数 般电工里遇到的周期函数都能满足 狄利赫利条件。 返回 上页 下页

13.2 周期函数分解为傅里叶级数  f t t   T ( ) d 0 若周期函数满足狄利赫利条件： ①周期函数极值点的数目为有限个； ②间断点的数目为有限个； ③在一个周期内绝对可积，即： 可展开成收敛的傅里叶级数 注意 一般电工里遇到的周期函数都能满足 狄利赫利条件。 返 回 上 页 下 页

周期函数展开成傅里叶级数： 直流分量 基波（和原 f(t)=A+A cos(@t+) 函数同频) +4mc0s(20,t+4,)+ 二次谐波 (2倍频) +A cos(not+)+ 高次谐波 f(t)=A,+∑Acos(kt+) 返回 上页 下页

直流分量 基波（和原 函数同频） 二次谐波 （2倍频） 高次谐波 ( ) cos( ) 1 0  1      k km k f t A A kt  f (t)  A0  A1m cos(1 t  1 )   A2m cos(21 t  2 )   A nm cos(n1 t  n )  周期函数展开成傅里叶级数： 返 回 上 页 下 页

也可表示成： A cos(ko,t+)=a cos ko,t+b sin ko,t 00 f(t)=a+>[a,cosko,t+bsin kot] k=1 系数之间的关系为： =a A 二个 aj+b a, FAmC0S b=-Am sin o =arctan -b 返回 上页 下页

( ) [ cos sin ] 1 1 0 1 f t a a k t b k t k k  k        A k t a k t b k t km 1  k  k 1  k 1 cos(   ) cos  sin  也可表示成： k k k k km k k km k km k k a b a A b A A a b A a         arctan cos sin 2 2 0 0    系数之间的关系为： 返 回 上 页 下 页

系数的计算： A=a=TSf(Odt a, f()cs(kd() 入 bk=· f(t)sin(kot)d(@,t) 求出4o、4、b便可得到原函数)的展开式。 返回 上页 下页

       2π 0 1 1 2π 0 1 1 0 0 0 ( )sin( )d( ) π 1 ( )cos( )d( ) π 1 ( )d 1 b f t k t t a f t k t t f t t T A a k k T     求出A0 、ak 、bk 便可得到原函数 f(t) 的展开式。 系数的计算： 返 回 上 页 下 页