
上浒充通大粤 SHANGHAI JIAO TONG UNIVERSITY 7.5 Enthalpy of mixing:ideal solution (1) d(△G)=-△SdT △G°=△H°-1△S The enthalpy of mixing of a solution, -rel Multiplying by 1/T,we obtain: T =风 ☐d9。=》。 d(△G) T For an ideal solution: G=RTInda=RTInxa 2g)=R)=ra dR血x4=F=0=万A-L4 aT dm The enthalpy of mixing of an ideal solution is zero: 且y=x47+xB万公=0 (ideal solution)
7.5 Enthalpy of mixing: ideal solution (1) d(1/T)

上浒充通大粤 SHANGHAI JIAO TONG UNIVERSITY 7.5 Enthalpy of mixing:ideal solution(2) Similarly,the volume change upon mixing, &G -rel =y and O = aP T There is error in textbook d(RTInxA)=V=0 dP M=x4F+xF=0 -rel rel To summarize,for an ideal solution: Gw=RT∑lhx HM=0 SM=-R∑yn Iy =0
7.5 Enthalpy of mixing: ideal solution (2) There is error in textbook

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 7.6 Graphical Representation (1) If we know a property of a two-component solution as a function of composition We can determine the partial molar values of that property. The molar volume of a solution can be determined simply by forming solutions of A and B with different compositions and measuring the resulting specific volume
7.6 Graphical Representation (1)
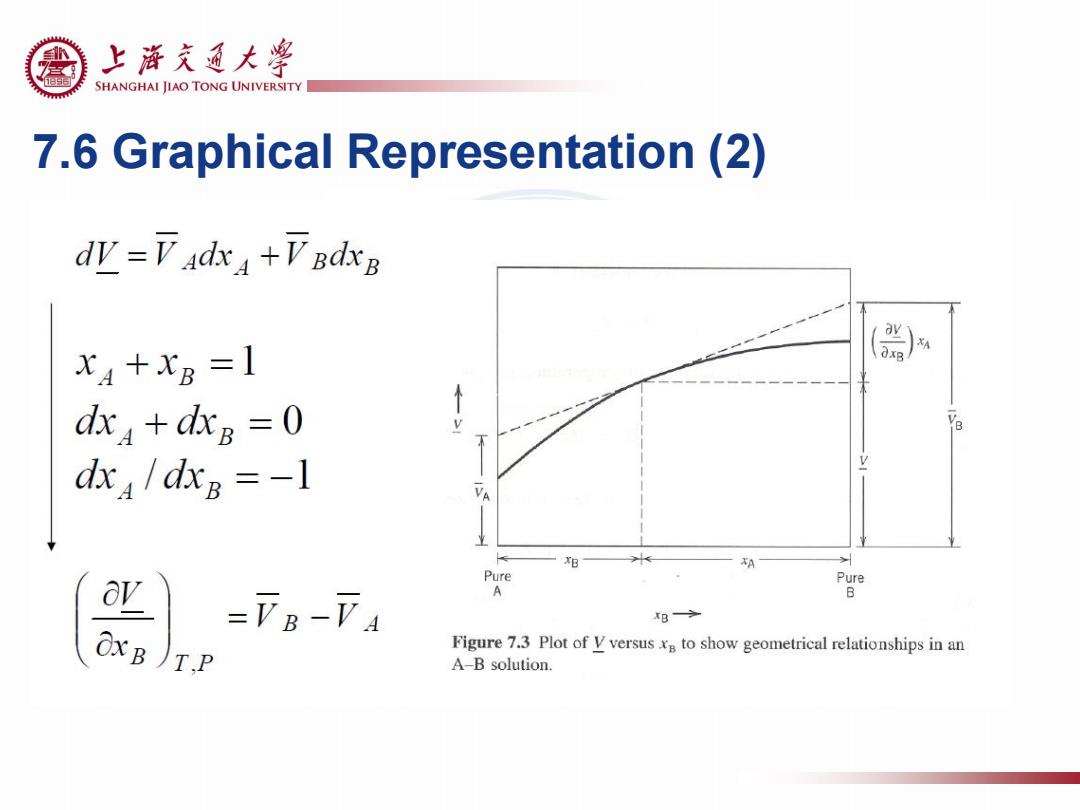
上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 7.6 Graphical Representation(2) dW=下Ad4+VBdxg x4+x8 =1 dx +dxg =0 dxa/dxB=-1 VA XB A Pure Pur A B Figure 7.3 Plot of V versus to show geometrical relationships in an A-B solution
7.6 Graphical Representation (2)

上游充通大¥ SHANGHAI JIAO TONG UNIVERSITY 7.6 Graphical Representation (3) d亚=F4d4+Vadx I. =XAVB-XAVA =VB-VA IⅡ. XB OxB)TP -xBVB-xBVA III. V=下AxA+FBxB A V=(a)+(b) 7B-7A =xB(VB-VA)+VA (a) =XBVB+XAVA A Pure Pu A B 8→ Figure 7.3 Plot of V versusxn to show geometrical relationships in an A-B solution
7.6 Graphical Representation (3) (a) (b)