电子科技大学：《高等电力系统分析》课程教学资源（课件讲稿）高等电力系统分析（PDF讲稿）

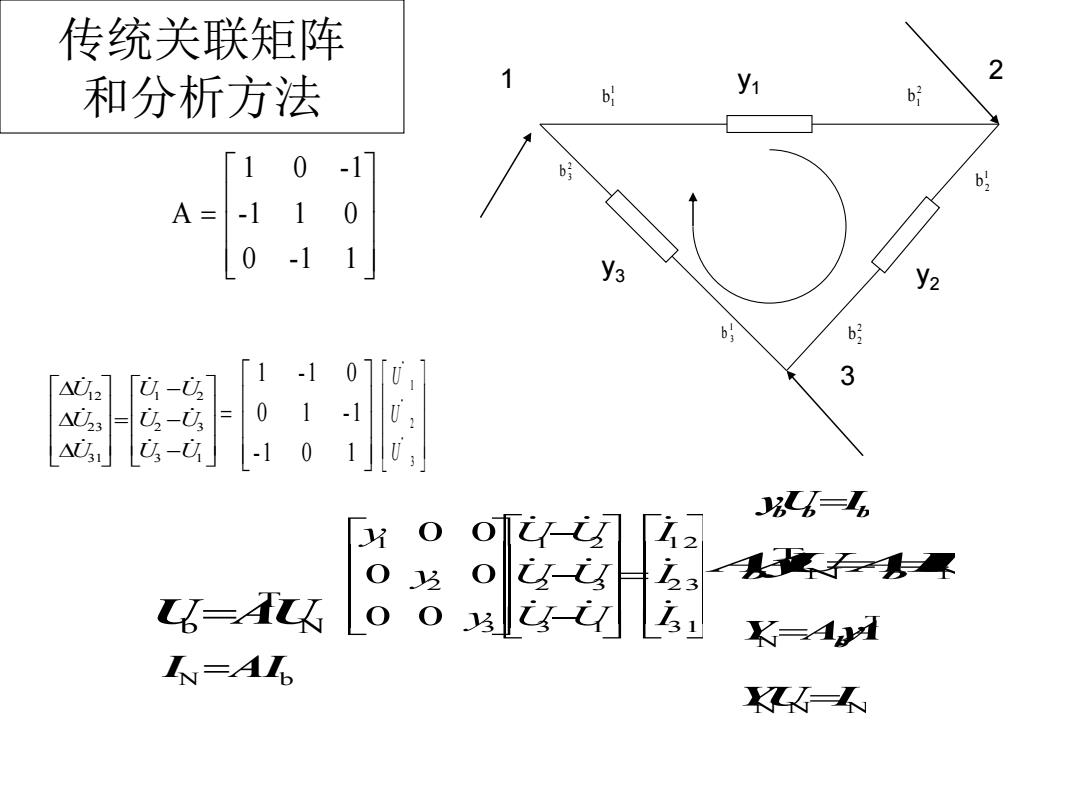
传统关联矩阵 2 和分析方法 b b好 10-1 A= -110 0-11 y2 b: b : 3 8=么 不不易界 K=1yl N=AI K

      3 1 2 3 1 2 3 1 2 3 1 2 3 2 10 0 0 0 0 0 III U U U U U U y y y        传统关联矩阵 和分析方法 1 0 -1 A -1 1 0 0 -1 1                 3 1 2 3 1 2 31 23 12 U U U U U U UUU          321 UUU 11 b 23 b 13 b 1 2 3 y 1 y 2 y 3 22 b 12 b 21 b N T UbA U IN A Ib ybUbIb N N T AybAUAIbI T YNAybA YNUNIN 1 -1 0 0 1 -1 -1 0 1           

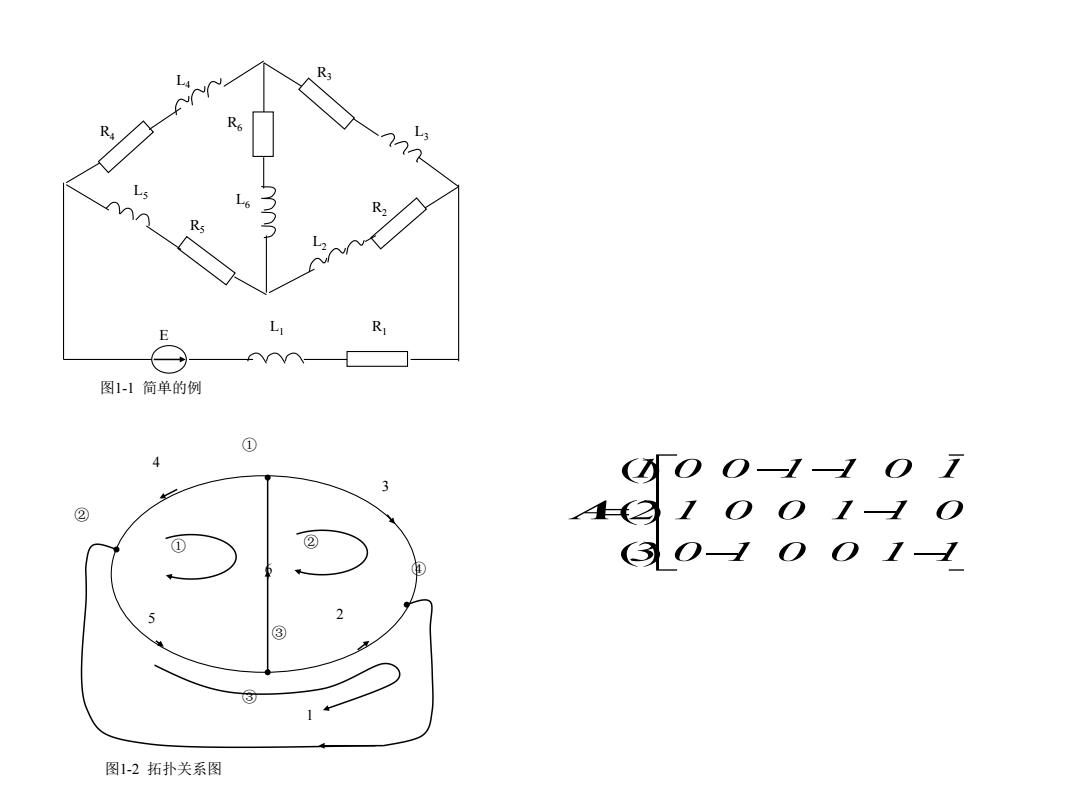
R nn 5 E R 图1-1简单的例 ① 4 7 3 ② ① ② 2 ③ 图1-2拓扑关系图

L4 R3 R4 L3 R6 R2 L2 R5 L5 L6 L1 R1 E 图1-1 简单的例 ① ② ③ ③ ① ② ④ 4 3 5 6 2 1 图1-2 拓扑关系图                 0 1 0 0 1 1 1 0 0 1 1 0 0 0 1 1 0 1 3 2 1 () () () A

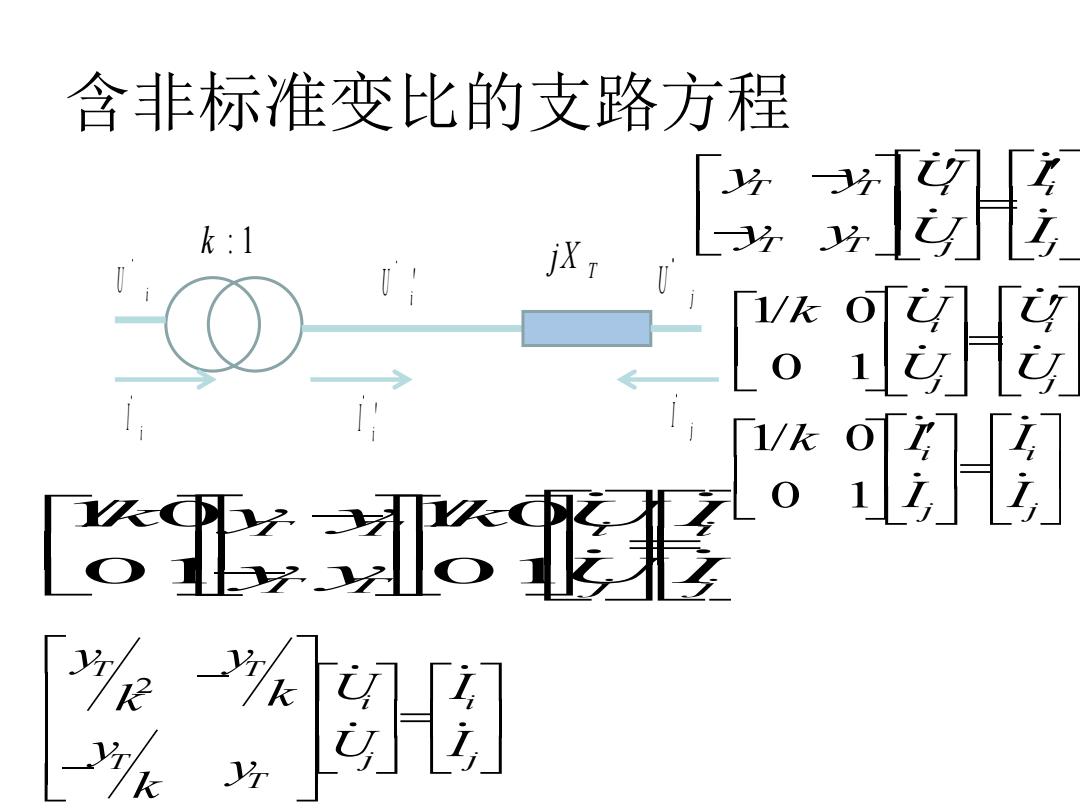
含非标准变比的支路方程 k:1 L形 1/k( 可之 1/k 6形

含非标准变比的支路方程 i U j U i U  i I j I i I  k : 1 T jX T T i i T T j j y y U I y y U I                       1/ 0 0 1 i i j j k U U U U                 1/ 0 0 1 i i j j k I I I I             1/ 0 1/ 0      01 01 T T i i T T j j k k y y U I y y U I                       2 T T i i T j j T y y k U I k y U I y k                         

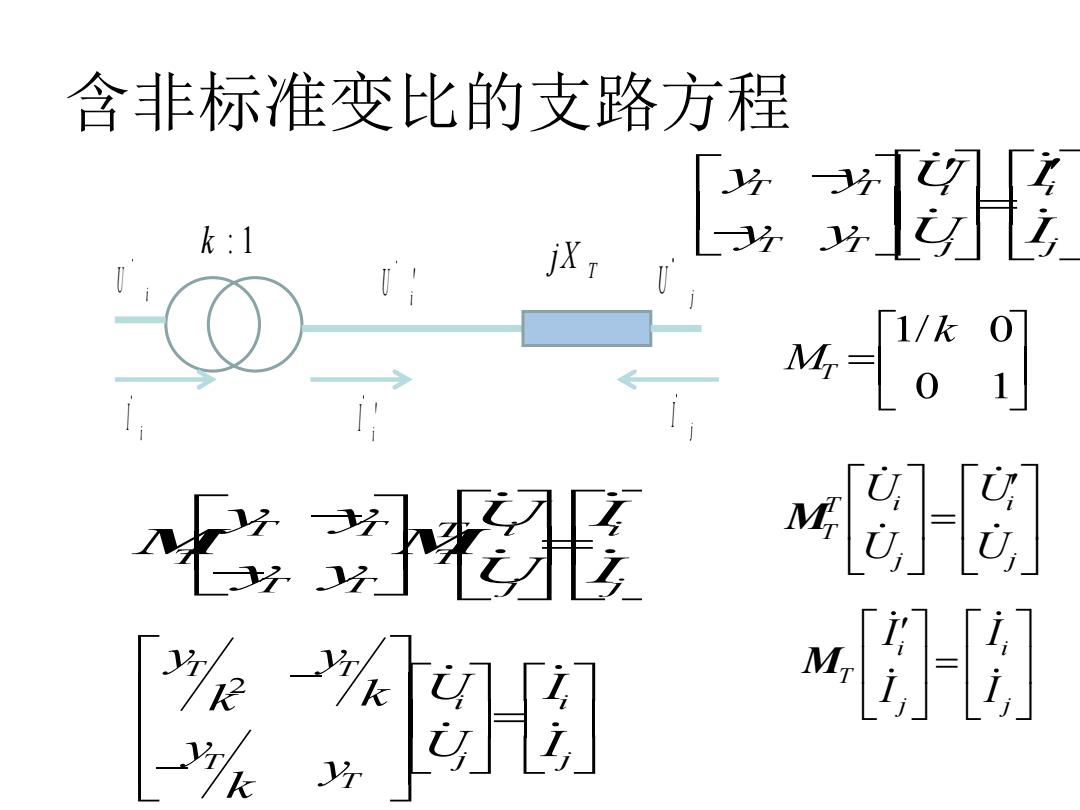
含非标准变比的支路方程 k:1 [ 40 形

含非标准变比的支路方程 i U j U i U  i I j I i I  k : 1 T jX T T i i T T j j y y U I y y U I                       T i i T j j U U U U              M i i T j j I I I I               M T T i i T T T T T j j y y U I y y U I                      M M 2 T T i i T j j T y y k U I k y U I y k                          1/ 0 0 1 T k M      

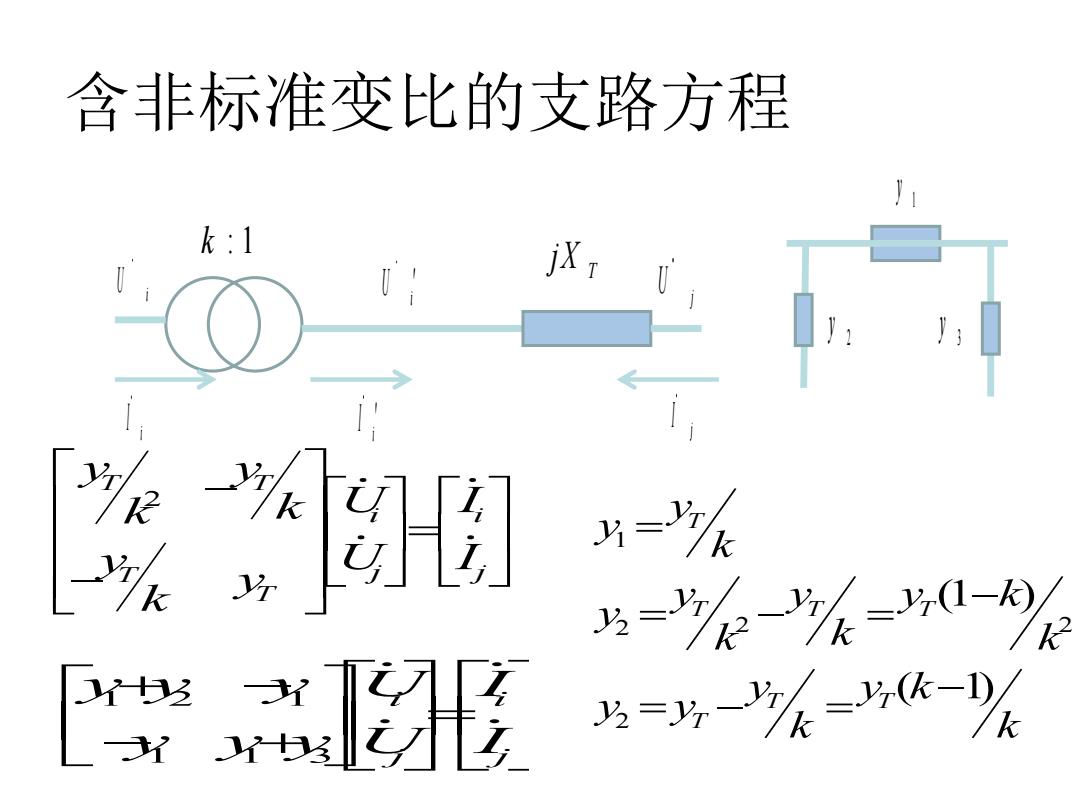
含非标准变比的支路方程 k:1 ( % =次 3--k-0- ”形 ⅓=y%--%

含非标准变比的支路方程 i U j U i U  i I j I i I  k : 1 T jX 2 T T i i T j j T y y k U I k y U I y k                          1 2 1 1 1 3 i i j j y y y U I y y y U I                       1 y 3 y 2 y 1 2 2 2 2 (1 ) ( 1) T T T T T T T y y k y y y k y k k k y y k y y k k         