内容要点 第一节变结构控制简介 先进控制技术 1变结构控制简介 变菊构控制是黄苏联学省Emelyanov于上世纪60年代提 2变结构控制理论基础 出的,经址k血等人的不断亮善,于70年代已发展成为 3变结构控制系统基本概念 控制铜减的一个相对微立的研克分文。该控制方法的大 优点是能够克景系能的不确定性,对系统套数变化、外 变结构控制 4滑动模态的存在条件与滑动模态方程 部干扰和来毫德动志具有很夏的鲁棒性,在机票人、款 5滑模变结构控制抖振问题 空敏天、电力革族、何康系峡等顺城海到丁广泛应用。 6滑模变结构控制系统设计 7滑模变结构控制应用 第一节变结构控制简介 第一节变结构控制简介 第一节变结构控制简介 1.1变结构控物(VSC)餐名 本质上最一美特辣的年赖性控制,其非蝴性麦现为烛 12滑勒模态定义 14滑模拉制代煮 制作用的不连续性。与其他拉侧搬培的不同之处:系峡 人为设电一经过平衡点的相轨速,遗过透当设计,暴 滑动模老可以设计且与对款参数和忧动无关具有快 的“帕构“并不圆定,而是在动老过程中,根提派镜当 峡状态点沿着武相轨迹渐近雅定到平海点。或形象地称为 速响皮、对查最变化和扰功不现敏(善摔性)、无须系峡 前的状本有目的地不新变化。 滑向平衡点的一种运功,滑孙视志的甲滑动二字即来测 在纳辨识、物通实现简单, 于此。 结构的变化著能唐功“滑功视态运功。称这操的 13系统纳构定义 1.5滑模控制铁点 控制为滑模控制。注意:不是所有的变结构2制那物滑 损控制,而滑慎控制是麦谢将池谢中康主流的设计方法。 系禁的一种模过即由某一龈量学方程捕述的机型, 当状志轨达滑动模酒后,难以严格沿着滑动模 意为承族的一种结构,系戴青几种不同的销构,款是说它 态面向平衡点滑功,而是在其两侧来回享她地造近平衡点, 所以,一殷将变结构拉制敏承为滑模拉制SMC,为 有几种(组)不同学餐达式表达的篱远。 从而产生抖振—滑模控制实示故用中的主受障两。 了突出变射构这个特点,可统称为滑模变结构控制。 1
1 先进控制技术 变结构控制 内容要点 1 变结构控制简介 2 变结构控制理论基础 3 变结构控制系统基本概念 4 滑动模态的存在条件与滑动模态方程 5 滑模变结构控制抖振问题 6 滑模变结构控制系统设计 7 滑模变结构控制应用 第一节 变结构控制简介 变结构控制是前苏联学者Emelyanov于上世纪60年代提 出的,经过Utkin等人的不断完善,于70年代已发展成为 控制领域的一个相对独立的研究分支。该控制方法的大 优点是能够克服系统的不确定性,对系统参数变化、外 部干扰和未建模动态具有很强的鲁棒性,在机器人、航 空航天、电力系统、伺服系统等领域得到了广泛应用。 第一节 变结构控制简介 1.1 变结构控制(VSC)概念 本质上是一类特殊的非线性控制,其非线性表现为控 制作用的不连续性。与其他控制策略的不同之处:系统 的“结构”并不固定,而是在动态过程中,根据系统当 前的状态有目的地不断变化。 结构的变化若能启动“滑动模态”运动,称这样的 控制为滑模控制。注意:不是所有的变结构控制都能滑 模控制,而滑模控制是变结构控制中最主流的设计方法。 所以,一般将变结构控制就称为滑模控制(SMC),为 了突出变结构这个特点,可统称为滑模变结构控制。 第一节 变结构控制简介 1.2 滑动模态定义 人为设定一经过平衡点的相轨迹,通过适当设计,系 统状态点沿着此相轨迹渐近稳定到平衡点,或形象地称为 滑向平衡点的一种运动,滑动模态的”滑动“二字即来源 于此。 1.3 系统结构定义 系统的一种模型,即由某一组数学方程描述的模型, 称为系统的一种结构,系统有几种不同的结构,就是说它 有几种(组)不同数学表达式表达的模型。 第一节 变结构控制简介 1.4 滑模控制优点 滑动模态可以设计且与对象参数和扰动无关,具有快 速响应、对参数变化和扰动不灵敏( 鲁棒性)、无须系统 在线辨识、物理实现简单。 1.5 滑模控制缺点 当状态轨迹到达滑动模态面后,难以严格沿着滑动模 态面向平衡点滑动,而是在其两侧来回穿越地趋近平衡点, 从而产生抖振——滑模控制实际应用中的主要障碍
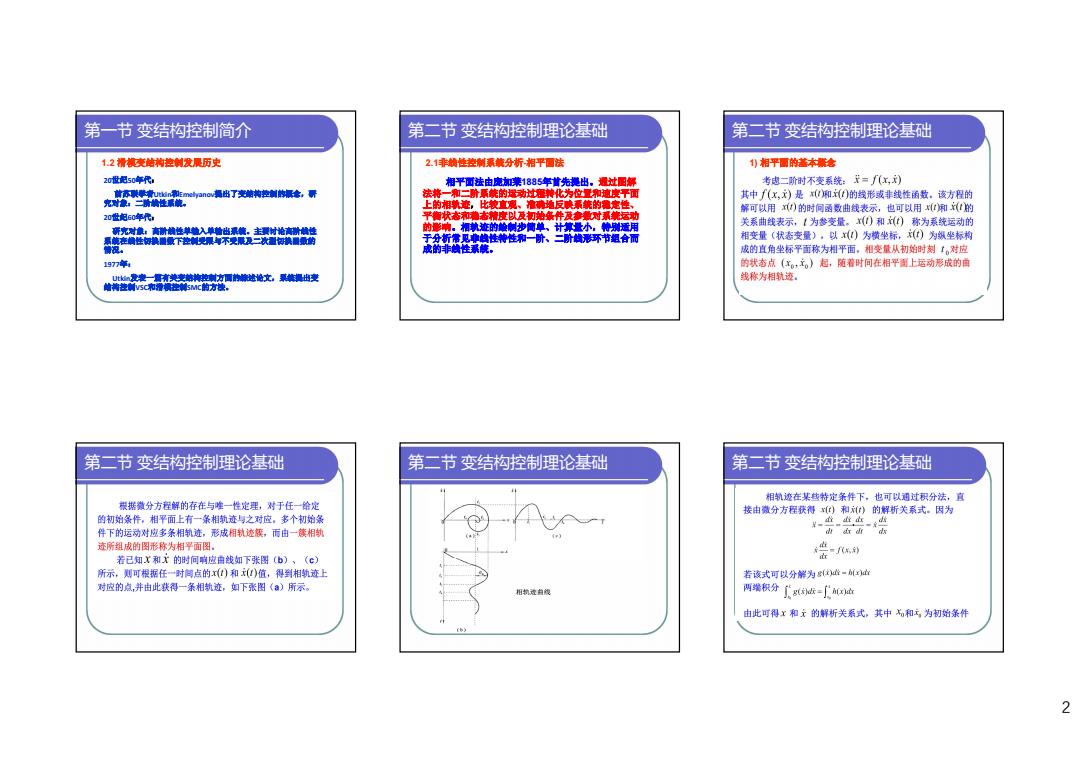
第一节变结构控制简介 第二节变结构控制理论基础 第二节变结构控制理论基础 1.2滑模变结构控制发展历史 2.1非龄性拉制承蒙分析相平圆法 )湘平面的落本景意 20世是50年代1 相平面法由虚谦1885年着先提出。漫过图解 考虑二阶时不变系统:开=f(x,) 九松表咖o清T支青 法将一和二阶系毓的动过化为位量和遮度平面 其中f(x,)是x闻)的形域非线性函数。该方程的 上的相轨迹,比较直风、推确地反映系毓的霜定性、 解可以用)的时间函数曲线表示,也可以用x州(的 20世的60年代: 平衡状态有者度以及打地条件及对抓运动 的童:相的制步单、计算量小,适用 关系曲线表示,1为参变量。x)和)称为系统运动的 所光+对业:新的性单地入单出票能。主预时地前性 在性的下控制不受及二次最的 于分析常见岭性物性和一阶、二阶形彩环节组合而 相变量(状态变量),以)为横坐标,()为纵坐标构 成的非性暴峡, 成的直角坐标平面称为相平面,相变量从初始时刻【。对应 1977年4 的状态点(x。,元。)起,随着时何在相平衡上运动形成的画 U瘦变一富南莫变结将地方间的造论文票装调出变 线称为相轨迹。 地岗注前V5和滑控MC的方妆, 第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 相轨迹在某些特定条样下,也可以通过积分法,直 根据微分方程解的存在与唑一性定理,对于任一给定 接由微分方程获得x)和)的解析关系式。因为 的初始条作,相平面上有一条相轨迹与之对应。多个初始氯 ¥止止血-出 件下的运动对应多条相轨迹,形成相轨迹簇,而由一篠相轨 山山 迹所组成的图形称为相平面图。 若已知X和X的时问响应由线如下张圆(b)、(c) 会 所示,则可根据任一时闯点的x)和()值,得到相轨迹上 若该式可以分解为g住心一x地 对应的点,并由此铁得一条相轨迹,如下张图(a)所示。 两端积分g话=广恤 由此可得x和云的解析关系式,其中和云,为初始条件 2
2 第一节 变结构控制简介 1.2 滑模变结构控制发展历史 20世纪50年代: 前苏联学者Utkin和Emelyanov提出了变结构控制的概念,研 究对象:二阶线性系统。 20世纪60年代: 研究对象:高阶线性单输入单输出系统。主要讨论高阶线性 系统在线性切换函数下控制受限与不受限及二次型切换函数的 情况。 1977年: Utkin发表一篇有关变结构控制方面的综述论文,系统提出变 结构控制VSC和滑模控制SMC的方法。 第二节 变结构控制理论基础 2.1非线性控制系统分析-相平面法 相平面法由庞加莱1885年首先提出。通过图解 法将一和二阶系统的运动过程转化为位置和速度平面 上的相轨迹,比较直观、准确地反映系统的稳定性、 平衡状态和稳态精度以及初始条件及参数对系统运动 的影响。相轨迹的绘制步简单、计算量小,特别适用 于分析常见非线性特性和一阶、二阶线形环节组合而 成的非线性系统。 第二节 变结构控制理论基础 1) 相平面的基本概念 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础
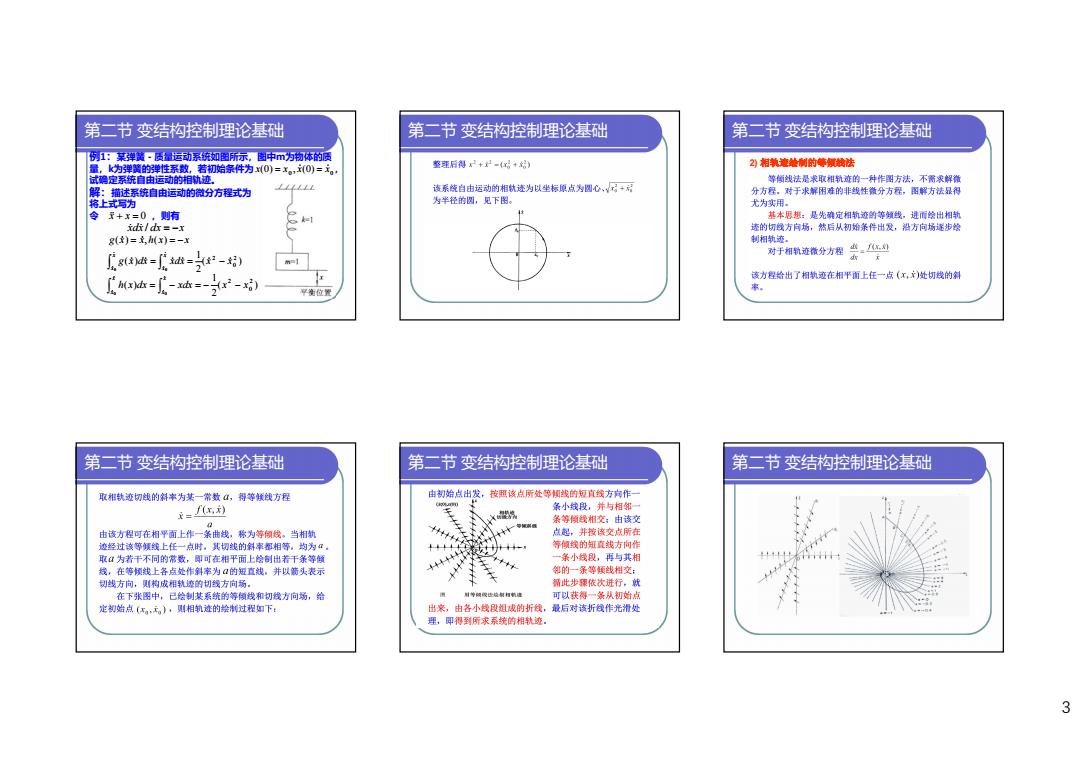
第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 例1:弹簧。质量运动系统如密所标示,韵中m为物体的质 量,k为弹簧的弹性系数,若初始条件为x(0)=x。,(0)=, 整递后得+-x+) 2)相教旋地制的等领输法 试确定系统自由运动的相轨迹。 等领线法是来取相轨迹的一种作图方法,不需求解微 解:描述系统自由运动的微分方程式为 该系饶自由运动的相轨迹为以坐标原点为圆心、√+用 分方程。对于求解困难的非线性微分方程,图解方法显得 将上式写为 为半轻的圆,见下图。 尤为实用。 令天+x=0,则有 基本思想:是先确定相轨迹的等领线。进而绘出相制 d/d止=-x 迹的切线方向场,然后从初始条件出爱,沿方向场逐步绘 ()=克,Mx)=-x 制相轨迹。 瓜-越=-划 对于相轨迹微分方程些。任 m-1 h=-h-对 该方程给出了相轨迹在相平面上任一点(x,)处切线的斜 平衡位 案。 第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 取相轨迹切线的斜案为某一常数:,得等领线方程 由初始点出发,按题该点所处等顿线的短直线方向作 R=x,初 条小线段,并与相细 由该方程可在相平面上作一条曲线。称为等倾线。当相轨 大a 条等倾线相交:由该交 点起,并按该交点所在 迹经过该等倾线上任一点时。其切线的斜率都相等。均为:。 等慎线的短直线方向作 取“为若干不同的常数,即可在湘平面上绘制出若干条等顿 一条小线段,再与其相 线,在等倾线上各点处作斜率为口的短直线。并以箭头表示 邻的一条等便线相交: 划线方向,则构成相轨迹的切线方向场。 痛此步骤依次进行,就 在下张图中,已绘制某系统的等倾线和切线方向场,给 目带阅现达地制有的速 可以获得一条从初始点 定初始点(,无),则相轨迹的绘彬过程如下: 出来,由各小线段姐减的折线,最后对该折线作光滑处 理,即得到所求系统的相轨迹。 3
3 第二节 变结构控制理论基础 例1:某弹簧-质量运动系统如图所示,图中m为物体的质 量,k为弹簧的弹性系数,若初始条件为 , 试确定系统自由运动的相轨迹。 解:描述系统自由运动的微分方程式为 将上式写为 令 ,则有 0 0 x(0) x , x(0) x x x 0 xdx dx x / g(x) x, h( x) x ( ) 2 1 ( ) 2 0 2 0 0 g x dx xdx x x x x x x ( ) 2 1 ( ) 2 0 2 0 0 h x dx xdx x x x x x x 第二节 变结构控制理论基础 第二节 变结构控制理论基础 2) 相轨迹绘制的等倾线法 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础

第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 使用等便法绘制相轨迹应注意以下儿点: 3)编性系统的相轨迹 1)坐标轴x和t应选用相同的比例尺,以便于根据等顿线 设系统初险条件为0=6,则0)=么,=一,相 斜率准确始制等横线上一点的相轨迹初线。 线性系筑是幸线性系统的特例,对于许多非线性一阶 迹如下图所示。 2)在相平西的上半平面,由于>0,则x随t增大而增 和二阶系绕(系统中所含非线性环节可用分段折线表示)。 由图可知,相轨迹位于过原点,解率为-1/门的直线上 当了>0时,相轨速沿该直线收数于原点:当T《0封, 加,相航迹的走向应是由左向右:在相平面的下华平面 常可以分成多个区间进行研究,面在各个区间内,幸线性 系统的运动特性可用钱性微分方程描述。 相轨迹沿该直线发散至无穷, ?<0,则x随1增大而或小,相轨迹的走向应由右向左。 3)除系统的平衡点外,相轨迹与x轴的相交点处切线斜率 《1)线性一阶系统的相轨迹 a=:,应为+D或-0,即相轨迹与轴重直相交. 描述线性一阶系统自由运动的微分方程为T心+C=0 4)一般地,等顿线分布越密,则所作的相轨迹越准确。但冠 所取等板线的增加,绘图工作量增加,同时也使作图产生 的积累误差增大。 连方为:子 第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 (2)线性二阶系统的轨迹 令心一心.:,可得等柄线方程为 下面就线性二阶微分方程参数<,b=0和b>0的七种不 描述线性二阶系统自由运动的微分方程为 )--bct)tct) 同情况加以具体讨论,其相物连曲线采用等倾线法或解析法 +he-0 住+ 给制面得, 当b>0时, 微分方程又可以表示为 其中k为等倾线的斜率,当:2-4奶>0,且b≠0时,可得 1)bc0,系饶特征根 t+25w正+@c=0 满足的两条特殊的等倾线,其斜率为 线性二阶系统的特征根 有++0 知=4=0=士-物,士可 2 如÷±06 2 2 该式表明,特殊的等倾线的斜率等于位于该等倾线上相 -8+5+0 82= 相轨迹微分方程为 轨迹任一点的切线斜率,即当相轨迹运动至特殊的等顿线上 51,8:为两个符号相反的互异实根。系统相平面图见下张图。 时,将沿着等顿线收敛或发收,而不可能税离该等倾线。 4
4 第二节 变结构控制理论基础 第二节 变结构控制理论基础 3) 线性系统的相轨迹 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础
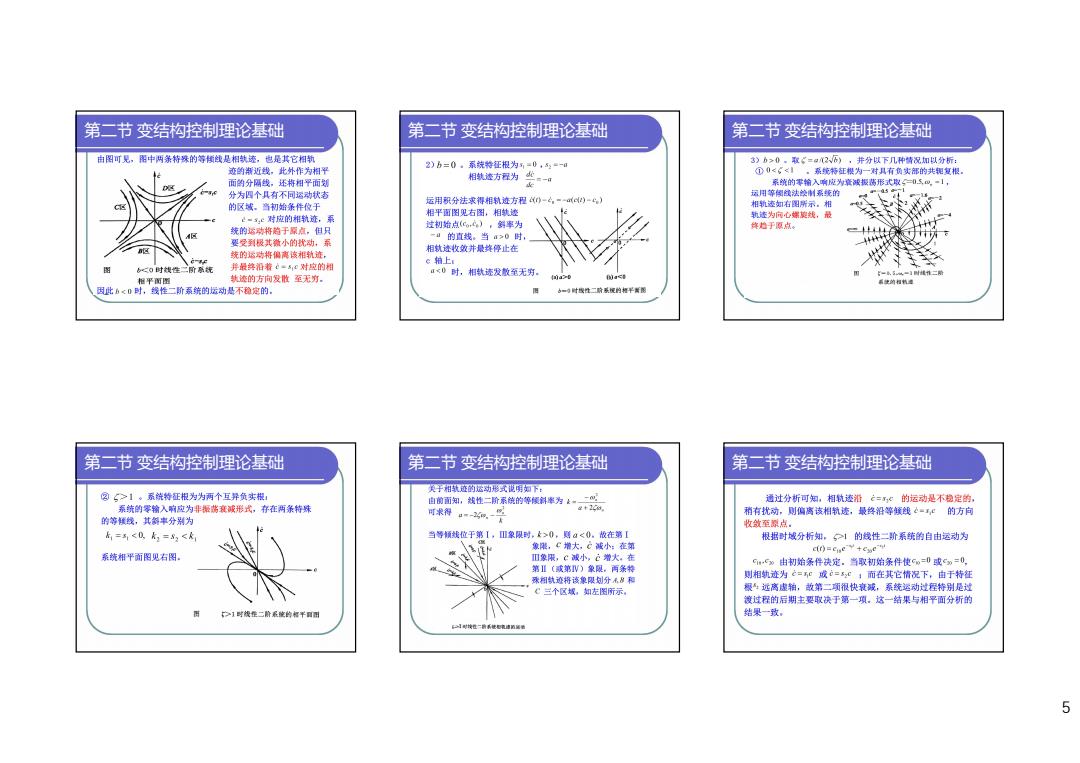
第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 由图可见,图中两杀特森的等横线是相轨迹,也是其它相轨 迹的晰近线,此外作为相平 2)乃=0。系辣特狂根为写=0,52=-日 3)b>0。取=a2、),并分以下几种情况知以分析: 面的分隔线。还将相平面划 相跳迹方程为空。口 ①0<6<!。系统特枉樱为一对具有负实部的共钜复根 系筑的零输入响成为章诚振药形式取=0S四,一1, 分为四个具有不同运动状老 远用等衡战法饶制系统的 运用积分法求得相轨迹方程(一心,=-)一4) 的区域。当初始条件位于 相机麦有可名图精示。相 相平面图见右图,相峡迹 正=3心对应的相轨迹,系 轨连为向心蝶旋线,最 过制始点(C,心),斜率为 统的运动将简于原点,但只 终趋于原点。 ”1的直线。当>0时 要受到极其微小的状动,系 相林迹收敛并最蜂停止在 统的运动将偏离该相轨迹, c轴上: <0时线性二阶系统 并最锌沿着心·5和对应的相 “<0时,相轨迹发散至无穷。 轨迹的方向爱收至无穷。 0a2-0 相平面图 属使的相机通 因此6《0时,线性二阶系筑的坛动悬不稳定的。 ■4时叶线性二阶系促的相平离 第二节变结构控制理论基础 第二节变结构控制理论基础 第二节变结构控制理论基础 子相载迹的远动地式追用知下: ②>1。系饶特征根为为两个互异负实根」 通过分折可知,相轨迹沿亡=心的运动是不稳定的, 系筑的零输入响应为非振荡衰或形式,存在两条特殊 由前面知,线性二阶系能的等候斜率为上。二心 可求得。0-受 ¥+248 稍有扰动,则偏离该相轨迹,最终沿等镶线一,:的方向 的等横线,其解率分别为 收敛至源点。 k1=51<0k1=82<k 当等领线位于第1,正象限时,k>0,则a<0。板在第I 根据时域分析知。>1的线性二阶系统的自由运动为 象限,增大,C诚小:在第 c(r)=cme+ewe 系统相平面图见右图。 D象限,C诚小,正增大。在 Gm”由初始条件决定。当取初始条件使C=0或0=0, 第Ⅱ(或第V)象限,两条转 骤相轨迹将该象限划分:品和 则相轨迹为=和或=5,C:而在其它情况下,由于特在 C三个区规,如左图所示, 极:远高虚轴,故第二项很快衰减,系统运动过程特别是过 渡过程的后期主要取决于第一项。这一结集与相平面分析的 >1时线二阶晨的平 结果一致 5
5 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础 第二节 变结构控制理论基础