电子科技大学：《高等电力系统分析》课程教学资源（课件讲稿）高等电力系统分析（PDF讲稿）

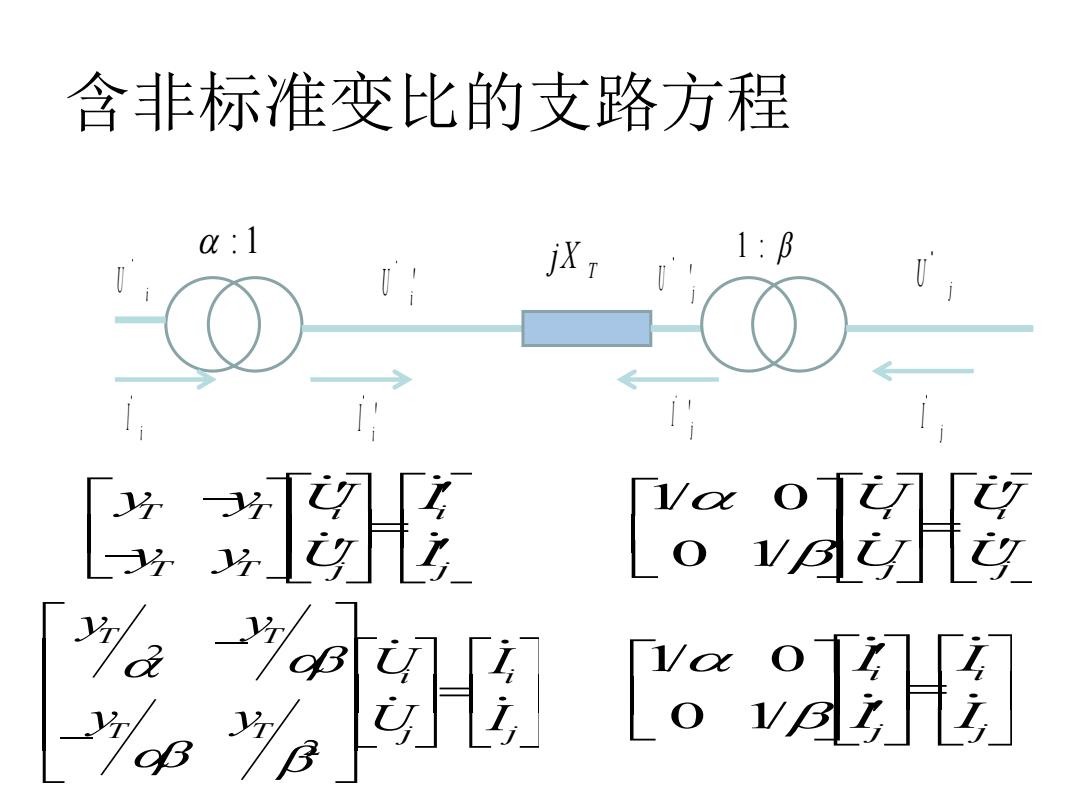
含非标准变比的支路方程 a:1 jX 1: [形 w 医形 L

含非标准变比的支路方程 i U j U  i U  i I j I  i I   :1 T jX T T i i T T j j y y U I y y U I                        1/ 0 0 1/ i i j j U U U U                    1/ 0 0 1/ i i j j I I I I                    j U j I 1 :  2 2 T T i i T T j j y y U I y y U I                           

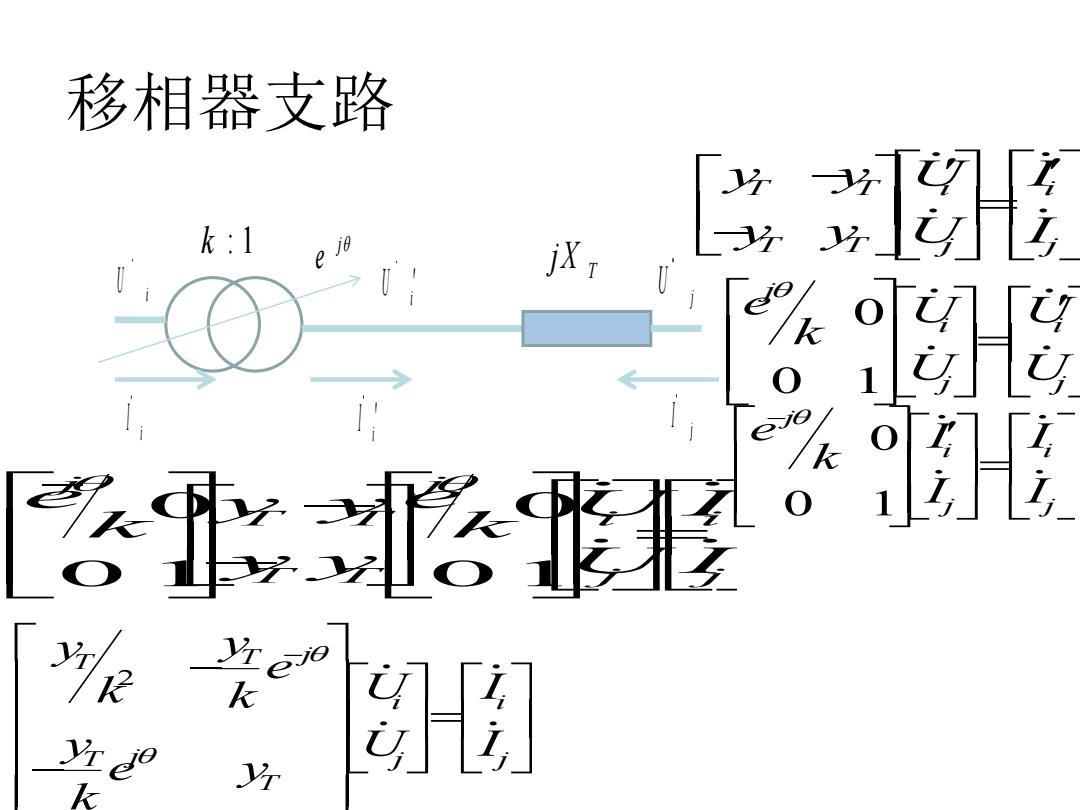
移相器支路 k:1 子亚形

移相器支路 i U j U i U  i I j I i I  k : 1 T jX T T i i T T j j y y U I y y U I                       0 0 1 j i i j j e U U k U U                    0 0 1 j i i j j e I I k I I              0 0        0 1 01 j j T T i i T T j j e e y y U I k k y y U I                             2 T T j i i T j j j T y y e k k U I y U I e y k                             j e 

关联矩阵的数学解释 迭加原理 LDR分解原理 补偿原理

关联矩阵的数学解释 • 迭加原理 • LDR分解原理 • 补偿原理

迭加原理 对于线性方程组 X 若A非奇异，其解 E 如果右边量可分解为下面的迭加形式 K B=∑B i=l 那么解向量也必然分解为 X-ZX X-=R i=1

若 非奇异，其解 迭加原理 对于线性方程组 AXB A XA 1 B 如果右边量可分解为下面的迭加形式 i K i B B 1   i K i X X 1  X 那么解向量也必然分解为 Xi ABi 1 

矩阵的LDR分解原理 01 012 ain A= 421 022 02n 0n2 0 0 012 07 00 1 0 a01…0+… 0 0 =l4,+l24252+…+ImnGna'm=∑l与4g

矩阵的LDR分解原理                                                                                           1 1 1 1 1 1 1 2 1 2 1 2 n n n n n n i j i j i j l a r l a r  l a r l a r                 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 1 1 2 1 1 1 2 1 2 2 1 2 2 2 1 1 1 2 1 a a a a a a a a a a a a a a A n n n n n n n n