
多机系统的静态稳定近似分析 一、简化和近似 由前几节对单机无穷大系统的静态稳定性分析可 知,如果要计及各种对发电机的影响因素(机械 阻力,电磁阻尼,励磁调节,电磁暂态过程), 即使是一台发电机也是相当复杂的。 。实际的系统中发电机台数很多,在工程计算中往 往采用一些简化的措施:
多机系统的静态稳定近似分析 一、简化和近似 由前几节对单机无穷大系统的静态稳定性分析可 知,如果要计及各种对发电机的影响因素(机械 阻力,电磁阻尼,励磁调节,电磁暂态过程), 即使是一台发电机也是相当复杂的。 实际的系统中发电机台数很多,在工程计算中往 往采用一些简化的措施:

① 对发电机进行简化 第一步:简化励磁调节的作用,认为E,为常数; 对励磁调节简化,假设励磁参数选择适当,不会引起系统失稳, 这时把发电机看作一个有恒定暂态电动势E,的电源, 不再计及调节器的影响。 第二步:为了方便计算,将E,恒定近似认为E恒定 为了计算方便,在工程实际中近似地认为发电机暂态电抗后的 电动势E'为常数 这样就将发电机简化为一个有恒定电动势E',内电抗为x,的电源

② 对负荷的近似处理 恒定阻抗模型Z,=R+X [Mw=k[a+(1-a)(1-sy] a会心c U'r. 2w 静态负荷模型 [P=a,+b,U+p,静态负荷=恒阻抗+恒电流+恒功率 Q=aU2+bU+c 综合负荷= 静态负荷 +电动机负荷 ↑ ↑ (功率与U,f成某一固定函数, (微分方程描述动态元件出现 不存在稳定问题) 扰动时,可能失稳) 为了近似计算,负荷以恒定阻抗来代表
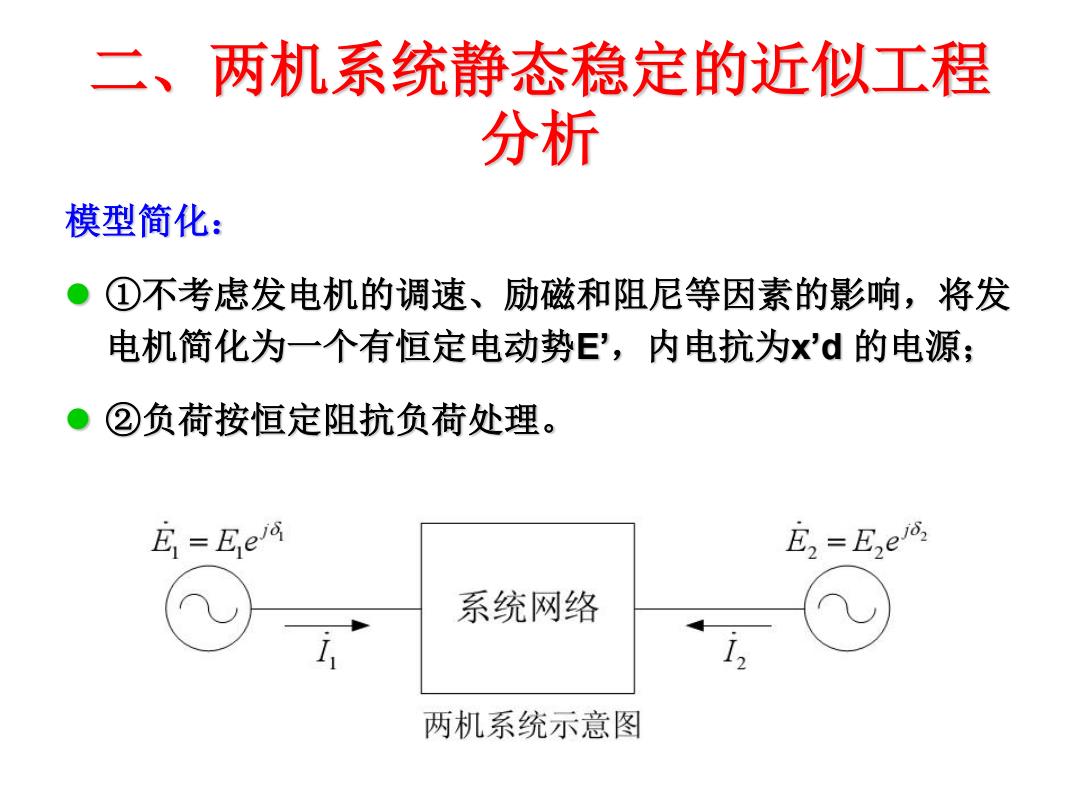
二、两机系统静态稳定的近似工程 分析 模型简化: ①不考虑发电机的调速、励磁和阻尼等因素的影响,将发 电机简化为一个有恒定电动势E',内电抗为x'd的电源; ②负荷按恒定阻抗负荷处理。 E=Ee 系统网络 1 两机系统示意图
二、两机系统静态稳定的近似工程 分析 模型简化: ①不考虑发电机的调速、励磁和阻尼等因素的影响,将发 电机简化为一个有恒定电动势E’,内电抗为x’d 的电源; ②负荷按恒定阻抗负荷处理
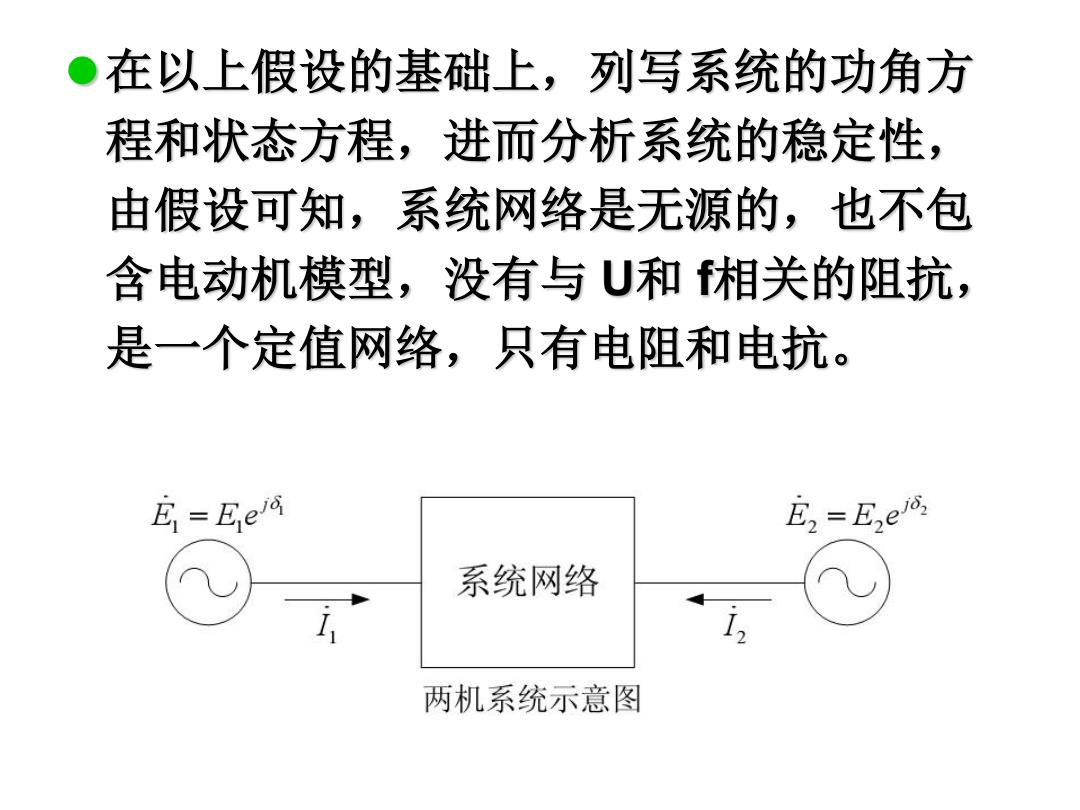
●在以上假设的基础上,列写系统的功角方 程和状态方程,进而分析系统的稳定性, 由假设可知,系统网络是无源的,也不包 含电动机模型,没有与U和相关的阻抗, 是一个定值网络,只有电阻和电抗。 E=Ee E2=Ee 系统网络 11 两机系统示意图
在以上假设的基础上,列写系统的功角方 程和状态方程,进而分析系统的稳定性, 由假设可知,系统网络是无源的,也不包 含电动机模型,没有与 U和 f相关的阻抗, 是一个定值网络,只有电阻和电抗