
(2)电容电压的连续性 从例7-2的计算结果可以看出,电容电流的波形是不 连续的矩形波,而电容电压的波形是连续的。从这个平滑 的电容电压波形可以看出电容电压是连续的一般性质。即 电容电流在闭区间t】有界时,电容电压在开区间(,)内 是连续的。这可以从电容电压、电流的积分关系式中得到 证明。 将仁T和仁T+dr代入式(6·3)中,其中t≤T<42和 t,<T+dt,得到 △=取,T+d-&,们=己打,(传n5→0当i(5有界时 !+dt
(2)电容电压的连续性 从例7-2的计算结果可以看出,电容电流的波形是不 连续的矩形波,而电容电压的波形是连续的。从这个平滑 的电容电压波形可以看出电容电压是连续的一般性质。即 电容电流在闭区间[t 1 ,t 2 ]有界时,电容电压在开区间(t 1 ,t 2 )内 是连续的。这可以从电容电压、电流的积分关系式中得到 证明。 将 t=T 和 t=T+dt 代入式 (6 - 3) 中 , 其 中 t 1<T<t 2 和 t 1<T+dt<t 2得到 ( )d 0 ( ) 1 ( d ) ( ) d C C i C d 0 当i 有界时 C u u T t u T T t T = + − = t → + →

当电容电流有界时,电容电压不能突变的性质,常用 下式表示 uc(t,)=uc(t_) 对于初始时刻=0来说,上式表示为 wc(0+)=uc(0_) (6-4) 利用电容电压的连续性,可以确定电路中开关发生作 用后一瞬间的电容电压值,下面举例加以说明
当电容电流有界时,电容电压不能突变的性质,常用 下式表示 对于初始时刻t=0来说,上式表示为 (0 ) (0 ) (6 4) uC + = uC − − ( ) ( ) C + = C − u t u t 利用电容电压的连续性,可以确定电路中开关发生作 用后一瞬间的电容电压值,下面举例加以说明
例7-3图7-8所示电路的开关闭合已久,求开关在=0时刻 断开瞬间电容电压的初始值4c(0+)。 t=0 图7-8 解:开关闭合已久,各电压电流均为不随时间变化的恒定 值,造成电容电流等于零,即 ()=Cd=0 dt
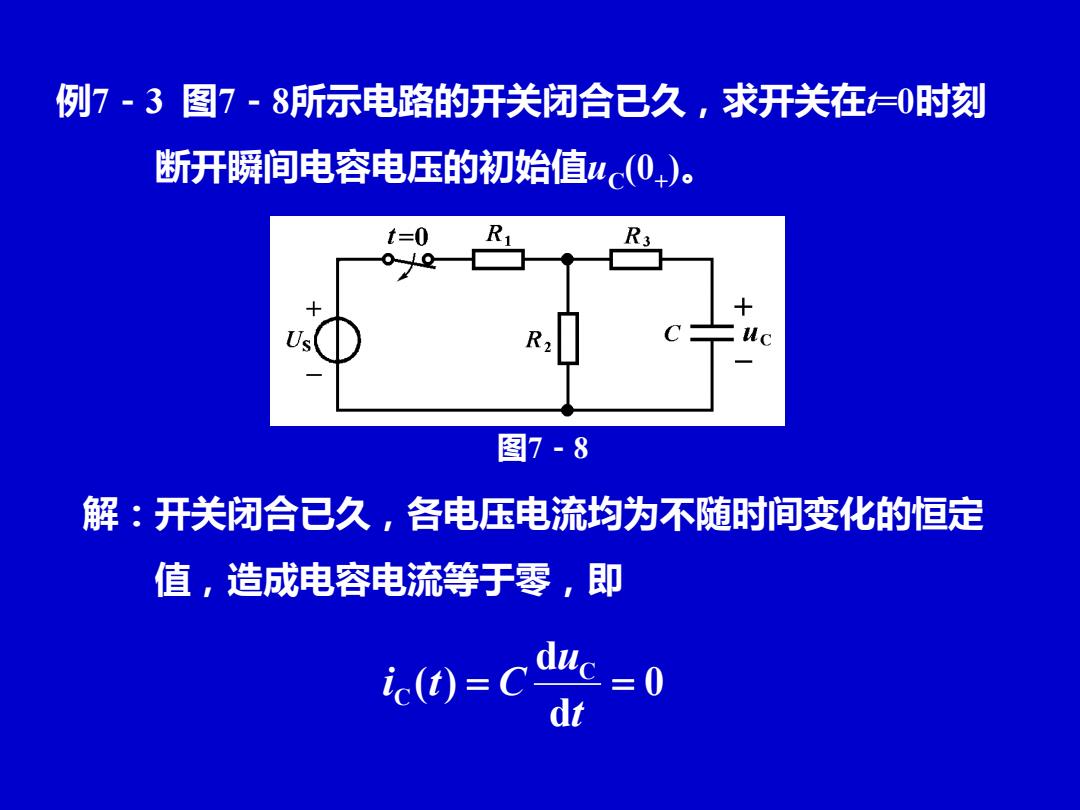
例7-3 图7-8所示电路的开关闭合已久,求开关在t=0时刻 断开瞬间电容电压的初始值uC (0+ )。 解:开关闭合已久,各电压电流均为不随时间变化的恒定 值,造成电容电流等于零,即 0 d d ( ) C C = = t u i t C 图7-8

t=0 Us 图7-8 电容相当于开路。此时电容电压为 uc(0)= R+R 当开关断开时,在电阻R和R3不为零的情况下,电容 电流为有限值,电容电压不能跃变,由此得到 he(0)=uc(0L)= R2-Us R+R2
电容相当于开路。此时电容电压为 S 1 2 2 C (0 ) U R R R u + − = 当开关断开时,在电阻R2和R3不为零的情况下,电容 电流为有限值,电容电压不能跃变,由此得到 S 1 2 2 C C (0 ) (0 ) U R R R u u + + = − = 图7-8
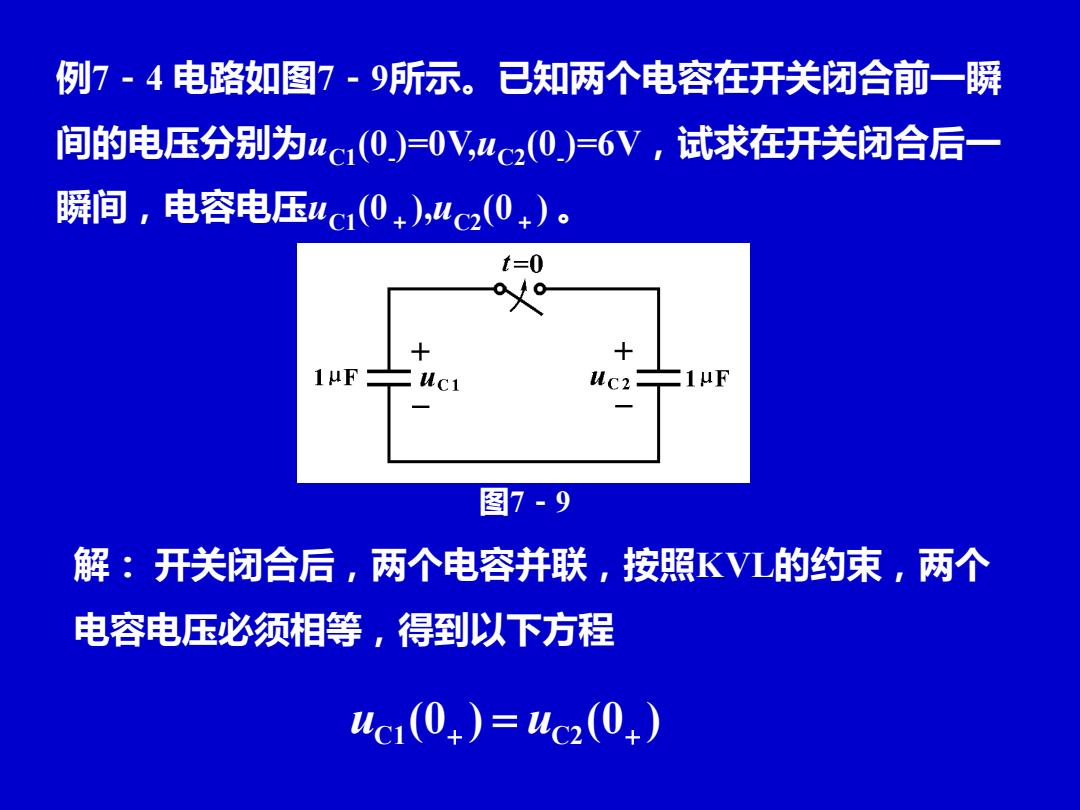
例7-4电路如图7-9所示。已知两个电容在开关闭合前一瞬 间的电压分别为uc1(0)=0V,4c2(0)=6V,试求在开关闭合后一 瞬间,电容电压uc1(0+),4c2(0+)。 t=0 1uF uc2 1uF 图7-9 解:开关闭合后,两个电容并联,按照KVL的约束,两个 电容电压必须相等,得到以下方程 uc1(0+)=uc2(0+)
例7-4 电路如图7-9所示。已知两个电容在开关闭合前一瞬 间的电压分别为uC1(0- )=0V,uC2(0- )=6V,试求在开关闭合后一 瞬间,电容电压uC1(0+),uC2(0+) 。 解: 开关闭合后,两个电容并联,按照KVL的约束,两个 电容电压必须相等,得到以下方程 图7-9 (0 ) (0 ) uC1 + = uC2 +