
原问题(P) 对偶问题(D) 目标max型 目标min型 有n个变量(非负) 有n个约束(大于等于) 有m个约束(小于等于) 有m个变量(非负) 价格系数 资源向量 资源向量 价格系数 技术系数矩阵 技术系数矩阵的转置
原问题(P) 对偶问题 (D) 目标max型 目标min型 有n个变量(非负) 有n个约束(大于等于) 有m个约束 (小于等于) 有m个变量(非负) 价格系数 资源向量 资源向量 价格系数 技术系数矩阵 技术系数矩阵的转置

原问题与对偶问题 直接写出例2一 线性规划问题的对偶问题 解:原问题的对偶问题为 min z 7x +4x2 -3x3 maxo=24y'+15y2+30y3 -4x1+2x2-6x3≤24 -4y3y2≥7 -3x1-6x2-7x3≥15 2y'6y2+5y3'=4 s.t. S.t. 5x2+3x3=30 6y-7y2+3为'≤-3 x1≤0,x2无约束,X3≥0 '≤0,y2≥0,y3无约束 2014-12-15 12
2014-12-15 12 原问题与对偶问题 直接写出例2——线性规划问题的对偶问题 解:原问题的对偶问题为 ' 0, 0, '无约束 6 ' 7 3 ' 3 2 ' 6 5 ' 4 4 ' 3y 7 . . max 24 ' 15 30 ' 1 2 3 1 2 3 1 2 3 1 2 1 2 3 y y y y y y y y y y st y y y 0, , 0 5 3 30 3 6 7 15 4 2 6 24 . . min 7 4 3 1 2 3 2 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x x x st z x x x 无约束

原问题与对偶问题 练习:写出下列线性规划问题的对偶问题 max Z=2x+3x2-5x3+x 4x1+x2-3x3+2x4≥5 3x1-2x2+7x4≤4 2x1+3x2+43+x4=6 x1≤0,x2,x3≥0,x4无约束 解:原问题的对偶问题为 minW =5y +4y2 +6y3 4y1+3y2-2y3≤2 y1-2y2+3y3≥3 -3y1+ 4y3≥-5 2y1+7y2+y3=1 2014-12-15 y1≤0,y2≥0,y3无约束 13
2014-12-15 13 原问题与对偶问题 练习:写出下列线性规划问题的对偶问题 1 2 3 4无约束 1 2 3 4 1 2 4 1 2 3 4 1 2 3 4 0, , 0, 2 3 4 6 3 2 7 4 4 3 2 5 max 2 3 5 x x x x x x x x x x x x x x x Z x x x x 解:原问题的对偶问题为 1 2 3 无约束 1 2 3 1 3 1 2 3 1 2 3 1 2 3 0, 0, 2 7 1 3 4 5 2 3 3 4 3 2 2 min 5 4 6 y y y y y y y y y y y y y y W y y y

§2原问题与对偶问题 学习要点: 1掌握原问题与其对偶问题的对应关系; 2.能熟练准确地写出一般形式的线性规划的对偶 问题。 作业:(P79)2.1(a,b) 2014-12-15 14
2014-12-15 14 §2 原问题与对偶问题 学习要点: 1.掌握原问题与其对偶问题的对应关系; 2.能熟练准确地写出一般形式的线性规划的对偶 问题。 作业: (P79) 2.1(a , b)
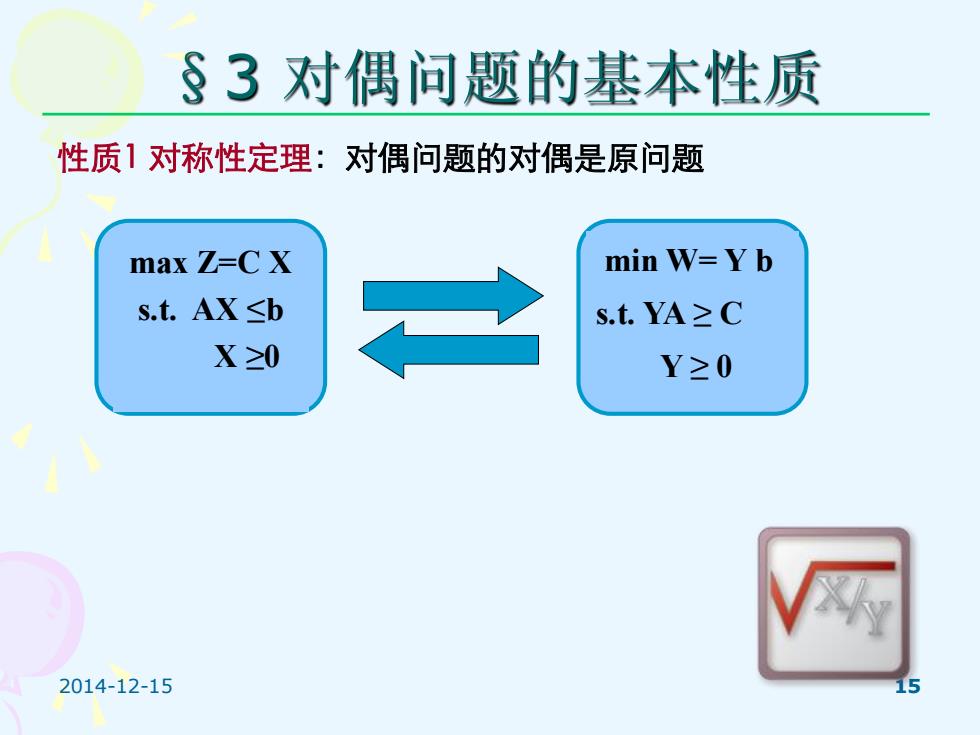
§3对偶问题的基本性质 性质1对称性定理:对偶问题的对偶是原问题 max Z=CX min W=Y b s.t.AX≤b s.t.YA≥C X≥0 Y≥0 2014-12-15
2014-12-15 15 §3 对偶问题的基本性质 性质1 对称性定理:对偶问题的对偶是原问题 min W= Y b s.t. YA ≥ C Y ≥ 0 max Z=C X s.t. AX ≤b X ≥0