
第四讲 函数的最值
第四讲 函数的最值

中值定理与导数应用 函数的最值 ●● 1.复习函数的极值 2.求函数最值的步骤 3.函数在区间上的最值 4.最值的应用问题
1. 复习函数的极值 2. 求函数最值的步骤 4. 最值的应用问题 函数的最值 3. 函数在区间上的最值

中值定理与导数应用 1.求函数极值的步骤 (1)先求函数的定义域D: (2)求函数的驻点即f'(xo)=0或f'(x1)不存在的点; (3)由D,x,x1划分区间,判定定理判定: (4)求极值,总结。 1
(2)求函数的驻点即 𝒇′ (𝒙𝟎 ) = 𝟎 ,或 𝒇 ′(𝒙𝟏 ) 不存在的点; (4)求极值,总结。 (1)先求函数的定义域𝑫; (3)由𝑫,𝒙𝟎 , 𝒙𝟏划分区间,判定定理判定; 1.求函数极值的步骤
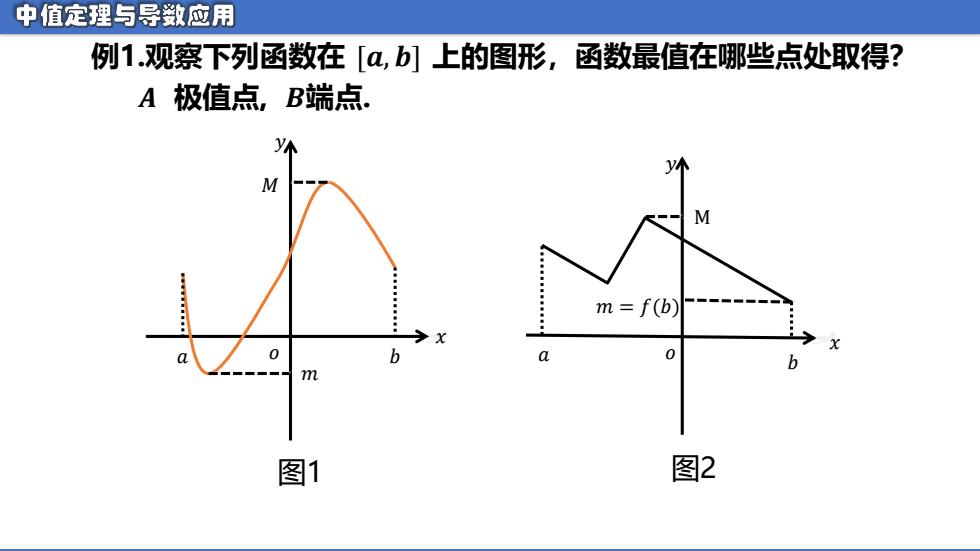
中值定理与导敛应用 例1.观察下列函数在「α,b]上的图形,函数最值在哪些点处取得? A极值点,B端点. M m=f(b) X 0 b m 图1 图2
𝑨 极值点, 𝑩端点. 𝑥 𝑦 𝑎 𝑜 𝑏 𝑀 𝑚 图1 𝑥 𝑦 𝑎 𝑜 𝑏 M 𝑚 = 𝑓(𝑏) 图2 例1.观察下列函数在 [𝒂, 𝒃] 上的图形,函数最值在哪些点处取得?

中值定理与导数应用 2.求函数在[α,b]上最值的步骤 (1)求函数的驻点即f'(xo)=0或f'(x1)不存在的点; (2)f(),f(x),f(a),f(b) (3)比较大小,总结
(1)求函数的驻点即𝒇′ (𝒙𝟎 ) = 𝟎,或𝒇 ′(𝒙𝟏 )不存在的点; (3)比较大小,总结。 (2)由𝒇(𝒙𝟎 ), 𝒇(𝒙𝟏 ), 𝒇(𝒂), 𝒇(𝒃) 2. 求函数在[𝒂, 𝒃]上最值的步骤