
第五讲 换元积分法
第五讲 换元积分法

不定积分 1.基本积分公式 (8) sinxdx =-cosx +c (1) kdx =kx+c (9) cosxdx sinx +c xu+1 (2) xudx= u+1 +c(u≠-1) (10) sec2xdx=tanx+c (3) -dx=Inx+c (11) csc2xdx =-cotx+c (4) exdx =ex+c (12) secxtanxdx secx +c Q (5) axdx +c(a>0,a≠1) Ina (13) cscxcotxdx =-cscx +c 1 1 (6) dx=-+c (14) dx arcsinx +c V1-x2 dx=2vx+c (15) dx arctanx +c 1+x2
(2) න 𝑥 𝑢𝑑𝑥 = 𝑥 𝑢+1 𝑢 + 1 + 𝑐 (𝑢 ≠ −1) (1) න 𝑘𝑑𝑥 = 𝑘𝑥 + 𝑐 (3) න 1 𝑥 𝑑𝑥 = 𝑙𝑛 |𝑥| + 𝑐 (4) න 𝑒 𝑥𝑑𝑥 = 𝑒 𝑥 + 𝑐 (5) න 𝑎 𝑥𝑑𝑥 = 𝑎 𝑥 𝑙𝑛𝑎 + 𝑐 (𝑎 > 0, 𝑎 ≠ 1) (6) න 1 𝑥 2 𝑑𝑥 = − 1 𝑥 + 𝑐 (9) න 𝑐𝑜𝑠𝑥𝑑𝑥 = 𝑠𝑖𝑛𝑥 + 𝑐 (8) න 𝑠𝑖𝑛𝑥𝑑𝑥 = −𝑐𝑜𝑠𝑥 + 𝑐 (10) න 𝑠𝑒𝑐2𝑥𝑑𝑥 = 𝑡𝑎𝑛𝑥 + 𝑐 (11) න 𝑐𝑠𝑐 2𝑥𝑑𝑥 = −𝑐𝑜𝑡𝑥 + 𝑐 (12) න 𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥𝑑𝑥 = sec𝑥 + 𝑐 (13) න 𝑐𝑠𝑐𝑥𝑐𝑜𝑡𝑥𝑑𝑥 = −𝑐𝑠𝑐𝑥 + 𝑐 (14) න 1 1 − 𝑥 2 𝑑𝑥 = 𝑎𝑟𝑐𝑠𝑖𝑛𝑥 + 𝑐 (15) න 1 1 + 𝑥 2 𝑑𝑥 = 𝑎𝑟𝑐𝑡𝑎𝑛𝑥 + 𝑐 (7) න 1 𝑥 𝑑𝑥 = 2 𝑥 + 𝑐 1.基本积分公式
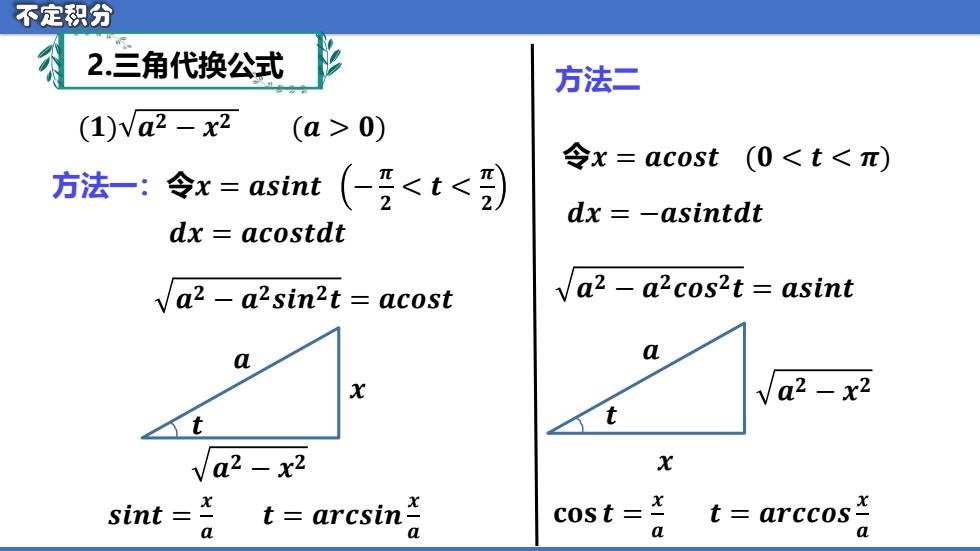
不定积分 2.三角代换公式 方法二 (1)Va2-x2 (a>0) 令x=acost(0<t<π) 方法-:令x=asint(-<t<罗 dx=-asintdt dx acostdt a2 -a2sin2t acost va2 a2cos2t asint a X Va2 -x2 t t Va2-x2 X sint t=arcsin cost= t=arccos a
(𝟏) 𝒂𝟐 − 𝒙 𝟐 (𝒂 > 𝟎) 方法一:令𝒙 = 𝒂𝒔𝒊𝒏𝒕 − 𝝅 𝟐 < 𝒕 < 𝝅 𝟐 𝒅𝒙 = 𝒂𝒄𝒐𝒔𝒕𝒅𝒕 𝒕 𝒔𝒊𝒏𝒕 = 𝒙 𝒂 𝒙 𝒂 𝒂𝟐 − 𝒙 𝟐 𝒂𝟐 − 𝒂𝟐𝒔𝒊𝒏𝟐𝒕 = 𝒂𝒄𝒐𝒔𝒕 𝒕 = 𝒂𝒓𝒄𝒔𝒊𝒏 𝒙 𝒂 令𝒙 = 𝒂𝒄𝒐𝒔𝒕 (𝟎 < 𝒕 < 𝝅) 𝒅𝒙 = −𝒂𝒔𝒊𝒏𝒕𝒅𝒕 𝒕 𝐜𝐨𝐬 𝒕 = 𝒙 𝒂 𝒙 𝒂 𝒂𝟐 − 𝒙 𝟐 𝒂𝟐 − 𝒂𝟐𝒄𝒐𝒔𝟐𝒕 = 𝒂𝒔𝒊𝒏𝒕 𝒕 = 𝒂𝒓𝒄𝒄𝒐𝒔 𝒙 𝒂 2.三角代换公式 方法二

不定积分 例1:∫V4-xZdx 解: x=2sint,dx 2costdt (<t< =∫2cost·2 costdt 2 dt x t 2t+sin2t+C V4-x2 =2t+2sintcost C sint x-2 =2 aresin+2登+c t=arcsin 2 aresin吃+4 V4-x2 X -+C cost= 2 2
�𝒅𝟐� :例1 𝟒 − 𝒙 解: 令𝒙 = 𝟐𝒔𝒊𝒏𝒕,𝒅𝒙 = 𝟐𝒄𝒐𝒔𝒕𝒅𝒕 �𝒅𝒕𝒔𝒐𝒄𝟐� ∙ �𝒔𝒐𝒄𝟐� = �� = 𝟏+𝒄𝒐𝒔𝟐𝒕 𝟐 𝒅𝒕 = 𝟐𝒕 + 𝒔𝒊𝒏𝟐𝒕 + 𝑪 = 𝟐𝒂𝒓𝒄𝒔𝒊𝒏 𝒙 𝟐 + 𝟐 ∙ 𝒙 𝟐 ∙ 𝟒−𝒙 𝟐 𝟐 + 𝑪 = 𝟐𝒂𝒓𝒄𝒔𝒊𝒏 𝒙 𝟐 + 𝒙 𝟒−𝒙 𝟐 𝟐 + 𝑪 = 𝟐𝒕 + 𝟐𝒔𝒊𝒏𝒕𝒄𝒐𝒔𝒕 + 𝑪 𝒔𝒊𝒏𝒕 = 𝒙 𝟐 𝒕 𝒙 𝟐 𝟒 − 𝒙 𝟐 𝒕 = 𝒂𝒓𝒄𝒔𝒊𝒏 𝒙 𝟐 𝒄𝒐𝒔 𝒕 = 𝟒−𝒙 𝟐 𝟐 − 𝝅 𝟐 < 𝒕 < 𝝅 𝟐

不定积分 (2)Wa2+x2 (a>0) 方法二 方法一:令x=atant(-7<t<爱 令x=acott (0<t<π) dx asec2tdt dx =-acsc2tdt a2 a2tan2t asect a2 a2cot2t acsct Va2 +x2 Va2 +x2 a t t a X Va2+x2 tant Va2+x2 sect cott = csct= a a a a
(𝟐) 𝒂𝟐 + 𝒙 𝟐 (𝒂 > 𝟎) 令𝒙 = 𝒂𝒕𝒂𝒏𝒕 (− 𝝅 𝟐 < 𝒕 < 𝝅 𝟐 ) 𝒅𝒙 = 𝒂𝒔𝒆𝒄𝟐 𝒕𝒅𝒕 𝒕 𝒕𝒂𝒏𝒕 = 𝒙 𝒂 𝒙 𝒂 𝒂𝟐 + 𝒙 𝟐 𝒂𝟐 + 𝒂𝟐𝒕𝒂𝒏𝟐𝒕 = 𝒂𝒔𝒆𝒄𝒕 令𝒙 = 𝒂𝒄𝒐𝒕𝒕 (𝟎 < 𝒕 < 𝝅) 𝒅𝒙 = −𝒂𝒄𝒔𝒄 𝟐 𝒕𝒅𝒕 𝒕 𝒄𝒐𝒕𝒕 = 𝒙 𝒂 𝒙 𝒂 𝒂𝟐 + 𝒙 𝟐 𝒂𝟐 + 𝒂𝟐𝒄𝒐𝒕𝟐𝒕 = 𝒂𝒄𝒔𝒄𝒕 𝒔𝒆𝒄 𝒕 = 𝒂𝟐+𝒙 𝟐 𝒂 𝒄𝒔𝒄 𝒕 = 𝒂𝟐+𝒙 𝟐 𝒂 方法二 方法一: