
第三讲 微积分基本公式
第三讲 微积分基本公式
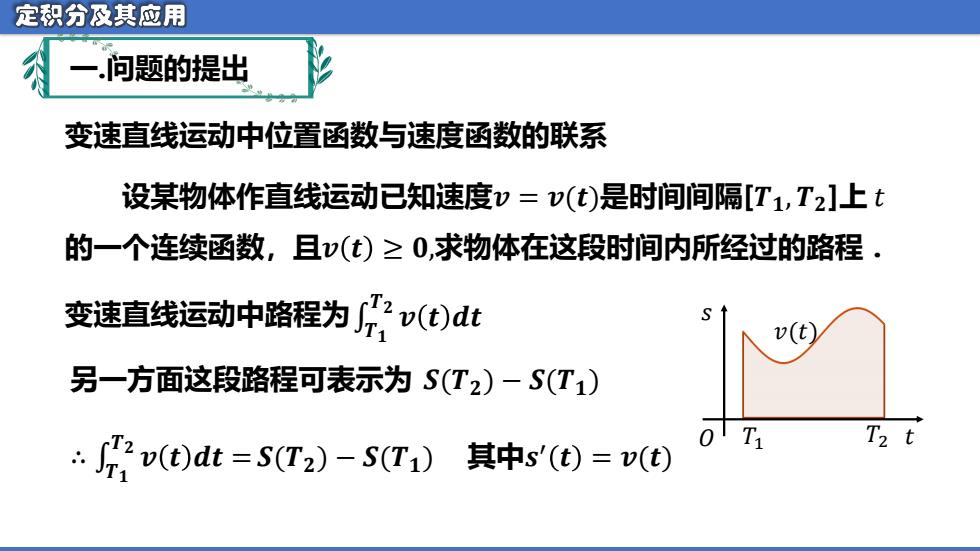
定积分及其应用 一问题的提出 变速直线运动中位置函数与速度函数的联系 设某物体作直线运动已知速度v=v(t)是时间间隔[T1,T2]上t 的一个连续函数,且v(t)≥0,求物体在这段时间内所经过的路程. 变速直线运动中路程为片v(t)dt 另一方面这段路程可表示为S(T2)-S(T1) v()dt=5(T2)-S(T1) 0T1 T2 t 其中s'(t)=v(t)
变速直线运动中位置函数与速度函数的联系 变速直线运动中路程为 另一方面这段路程可表示为 设某物体作直线运动已知速度𝒗 = 𝒗(𝒕)是时间间隔[𝑻𝟏, 𝑻𝟐]上 𝑡 的一个连续函数,且𝒗 𝒕 ≥ 𝟎,求物体在这段时间内所经过的路程 . �𝑻� 𝑻𝟐 𝒗 𝒕 𝒅𝒕 𝑺(𝑻𝟐) − 𝑺(𝑻𝟏) �𝑻� ∴ 𝑻𝟐 𝒗 𝒕 𝒅𝒕 = 𝑺(𝑻𝟐) − 𝑺(𝑻𝟏) 其中𝒔 ′ 𝒕 = 𝒗(𝒕) 一.问题的提出 𝑇1 𝑇2 𝑡 𝑠 𝑂 𝑣(𝑡)

定积分及其应用 二积分上限函数及其导数 设函数f(x)在区间[a,b]上连续,并且设x为[a,b]上的一点, 考察积分 fe)a=人redr 如果上限x在区间[a,b]上任意变动,则对于每个取定的x值, 定积分有一个对应值,所以它在a,b1上定义了一个函数, 记Φ(x)=f(t)dt积分上限函数
记𝚽(x)= �� 𝒙 𝒇 𝒕 𝒅𝒕 积分上限函数 设函数𝒇(𝒙)在区间[𝒂, 𝒃]上连续,并且设𝒙为[𝒂, 𝒃]上的一点, 考察积分 න 𝑎 𝑥 𝑓 𝑥 𝑑𝑥 =න 𝑎 𝑥 𝑓 𝑡 𝑑𝑡 如果上限𝒙在区间[𝒂, 𝒃]上任意变动,则对于每个取定的𝒙值, 定积分有一个对应值,所以它在[𝒂, 𝒃]上定义了一个函数, 二.积分上限函数及其导数
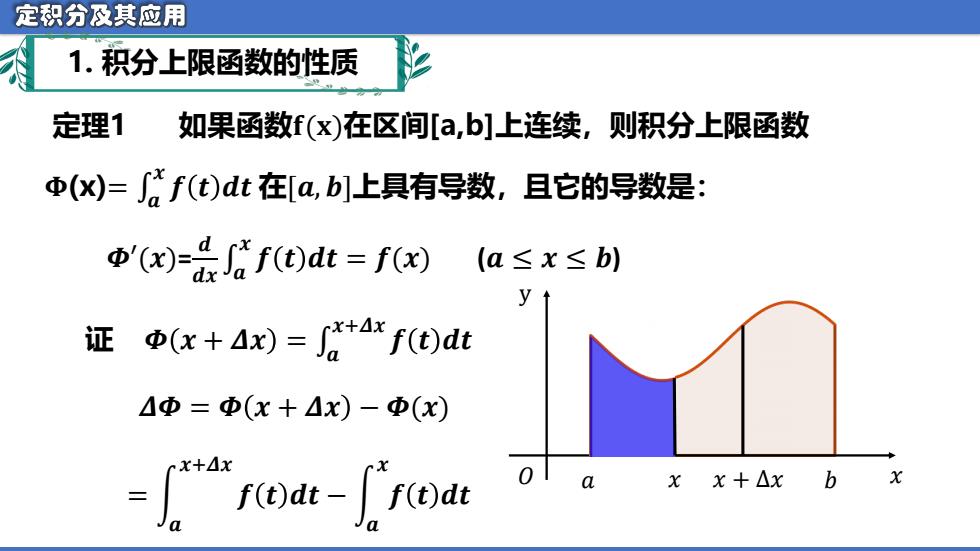
定积分及其应用 1.积分上限函数的性质 定理1 如果函数f(x)在区间[a,b]上连续,则积分上限函数 中(x)=f(t)dt在[a,b]上具有导数,且它的导数是: f(t)dt=f(x) (a≤x≤b) y 证中(x+Ax)=+4xf(t)dt △Φ=中(x+△x)-中(x) fat-roat a Xx+△xb X
证 定理1 如果函数𝐟(𝐱)在区间[a,b]上连续,则积分上限函数 �� =(x𝚽( 𝒙 𝒇 𝒕 𝒅𝒕 在[𝒂, 𝒃]上具有导数,且它的导数是: 𝜱′(𝒙)= 𝒅 �� �𝒅� 𝒙 𝒇 𝒕 𝒅𝒕 = 𝒇(𝒙) (𝒂 ≤ 𝒙 ≤ 𝒃) 𝑥 y 𝑂 𝑎 𝑥 𝑥 + Δ𝑥 𝑏 �� = �𝜟� + �� �� 𝒙+𝜟𝒙 𝒇 𝒕 𝒅𝒕 𝜟𝜱 = 𝜱 𝒙 + 𝜟𝒙 − 𝜱(𝒙) Φ(x) = න 𝒂 𝒙+𝜟𝒙 𝒇 𝒕 𝒅𝒕 − න 𝒂 𝒙 𝒇 𝒕 𝒅𝒕 1. 积分上限函数的性质
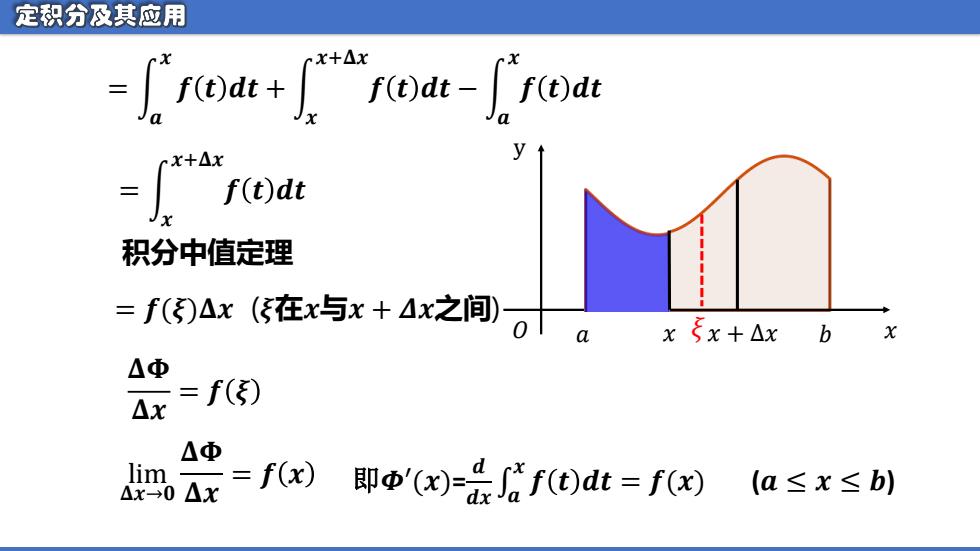
定积分及其应用 x+△x -roa+roa-roa X+△X = f(t)dt 积分中值定理 =f()Ax(在x与x+4x之间)O x5x+△x b △Φ △x =f() △Φ lim. △x-0△X =f(x) 即Φ'(cx)fd)dt=f) (a≤x≤b)
𝑥 y 𝑂 𝑎 𝑥 𝑥 + Δ𝑥 𝑏 Φ(x) = න 𝒂 𝒙 𝒇 𝒕 𝒅𝒕 + න 𝒙 𝒙+𝚫𝒙 𝒇 𝒕 𝒅𝒕 − න 𝒂 𝒙 𝒇 𝒕 𝒅𝒕 = න 𝒙 𝒙+𝚫𝒙 𝒇 𝒕 𝒅𝒕 = 𝒇(𝝃)𝚫𝒙 (𝝃在𝒙与𝒙 + 𝜟𝒙之间) 𝚫𝚽 𝚫𝒙 = 𝒇 𝝃 lim 𝚫𝒙→𝟎 𝚫𝚽 𝚫𝒙 = 𝒇 𝒙 即𝜱′(𝒙)= 𝒅 �� �𝒅� 𝒙 𝒇 𝒕 𝒅𝒕 = 𝒇(𝒙) (𝒂 ≤ 𝒙 ≤ 𝒃) 积分中值定理 𝜉