
第三讲 微积分基本公式
定积分及其应用 第三讲 微积分基本公式
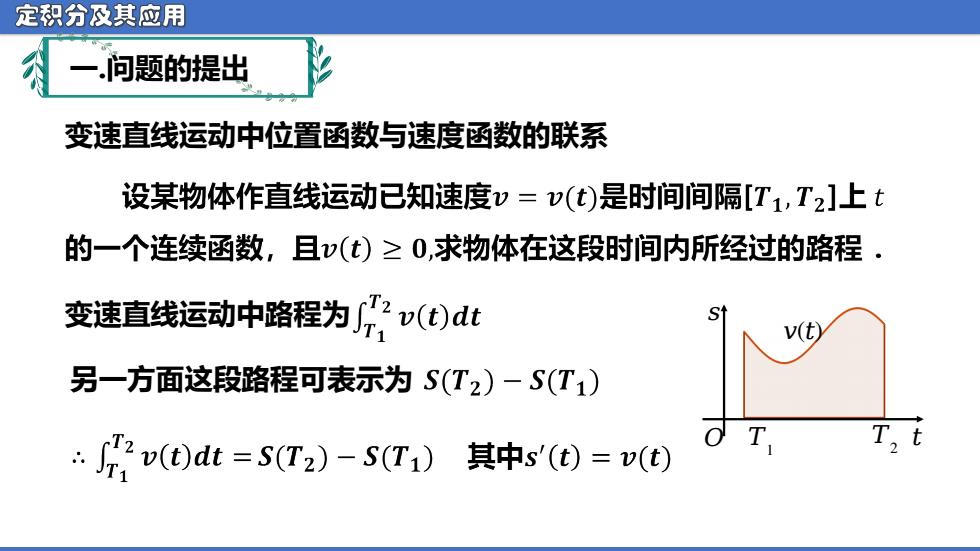
定积分及其应用 一问题的提出 变速直线运动中位置函数与速度函数的联系 设某物体作直线运动已知速度v=v(t)是时间间隔[T1,T2]上t 的一个连续函数,且v(t)≥0,求物体在这段时间内所经过的路程. 变速直线运动中路程为片v(d)dt S v(t) 另一方面这段路程可表示为S(T2)一S(T1) 2v()dt=5(T2)-S(T1) 其中s'(t)=v(t) O T T,t
定积分及其应用 变速直线运动中位置函数与速度函数的联系 变速直线运动中路程为 另一方面这段路程可表示为 一.问题的提出 ᵄ ᵆ 1 ᵄ 2 ᵆ ᵄ ᵆ (ᵆ)

定积分及其应用 二积分上限函数及其导数 设函数f(x)在区间[a,b]上连续,并且设x为[a,b]上的一点, 考察积分 FF(dt 如果上限x在区间[a,b]上任意变动,则对于每个取定的x值, 定积分有一个对应值,所以它在[α,b]上定义了一个函数, 记中(x)=∫f(t)dt积分上限函数
定积分及其应用 积分上限函数 二.积分上限函数及其导数
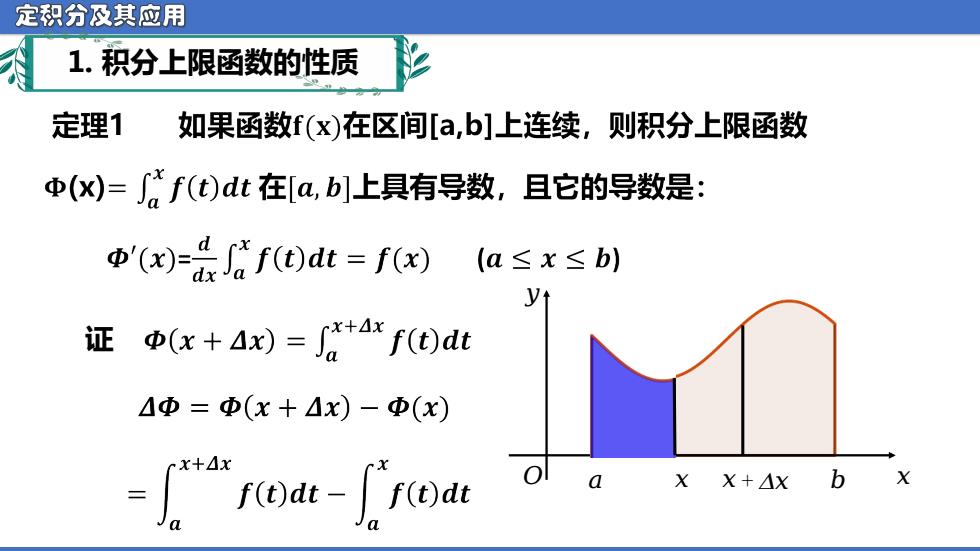
定积分及其应用 1.积分上限函数的性质 定理1 如果函数f(x)在区间[a,b]上连续,则积分上限函数 中(x)=f(t)dt在[a,b]上具有导数,且它的导数是: (xf(t)dt=f(x) (a≤x≤b) 证中(x+Ax)=+arf(d)dt △Φ=Φ(x+△x)-中(x) -f"rodt-frod XX+△Xb
定积分及其应用 证 ᵆ ᵆ ᵄ ᵄ ᵆ ᵆ + ᵮ ᵆ ᵄ ᵯ (x) 1. 积分上限函数的性质
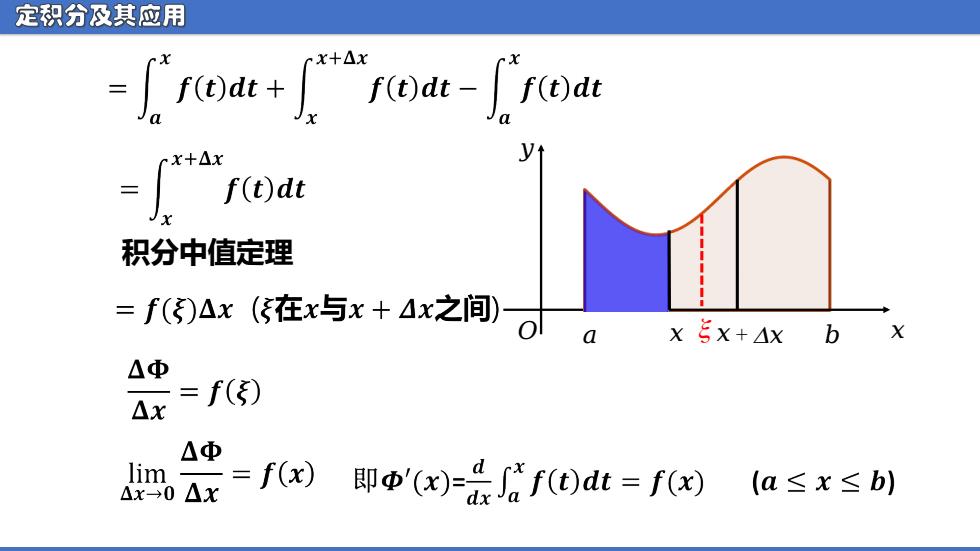
定积分及其应用 X+△x =faa+厂foi-Ka x+△x f(t)dt 积分中值定理 =f()△x(在x与x+△x之间) 0a xξX+△xb △Φ =f() △X △Φ Ar 0 Ax lim =f(x) 即p'(x)=Jf(t)dt=f(x) (a≤x≤b)
定积分及其应用 ᵆ ᵆ ᵄ ᵄ ᵆ ᵆ + ᵮ ᵆ ᵄ 积分中值定理 ᵯ (x) ᵰ