
·Independent X1,,Xn∈{0,l}with X=∑X,andh=EX] =1 Markov for MGF: (for any 1>0) Eix] Pr[X≥(1+ò]≤eaI+on e1ww-气aa) (when2=ln(1+δ) ·Bound MGF: -[i网-esw i运1 。Optimization: (e-1-(1+δ))achieves Min at stationary point九=ln(1+δ)
• Markov for MGF: • Bound MGF: • Independent with and X1,…, Xn ∈ {0,1} X = n ∑ i=1 Xi μ = 피[X] Pr[ X ≥ (1 + δ)μ ] (for any λ > 0) ≤ 피 [eλX ] eλ(1+δ)μ 피 [eλX ] = 피 [ n ∏ i=1 eλXi ] = n ∏ i=1 피 [eλXi ] ≤ e(eλ −1)μ ≤ e(eλ −1−λ(1+δ))μ • Optimization: (e achieves Min at stationary point λ − 1 − λ(1 + δ)) λ = ln(1 + δ) = ( eδ (1 + δ)(1+δ) ) μ (when λ = ln(1 + δ))
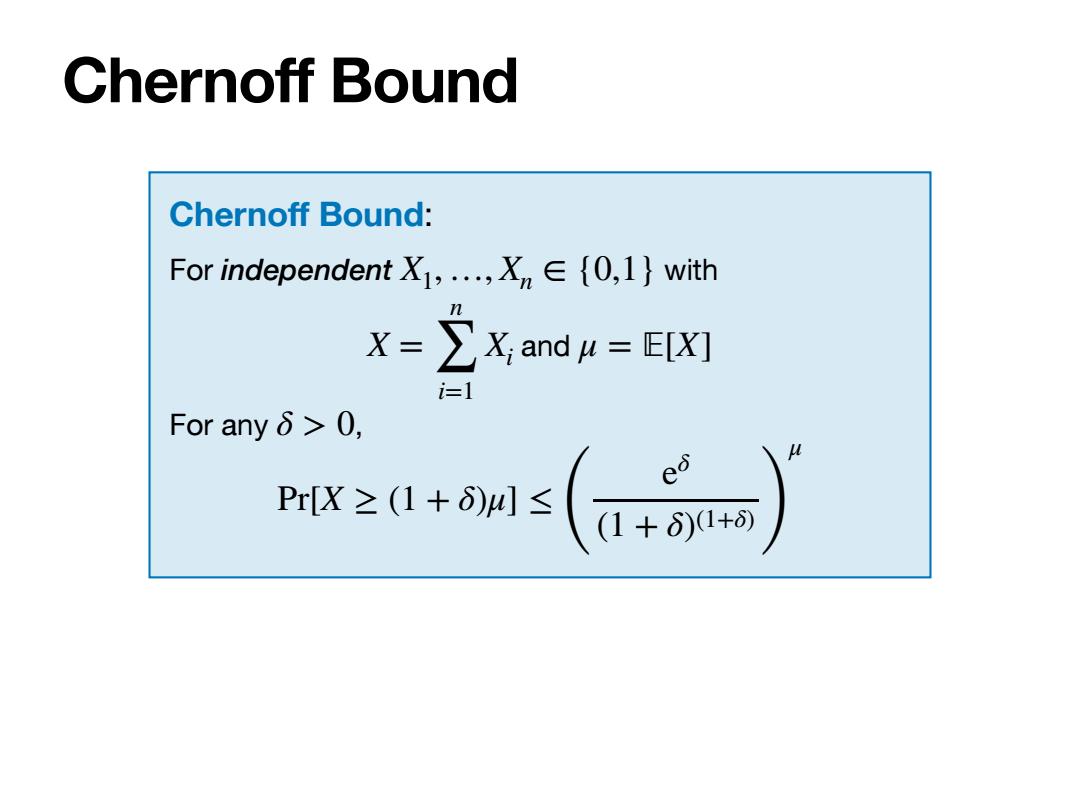
Chernoff Bound Chernoff Bound: For independent X,,Xn∈{0,l}with X-∑;and=E[X灯 i=1 For anyδ>0, xass(可
Chernoff Bound Chernoff Bound: For independent with and For any , X1, …, Xn ∈ {0,1} X = n ∑ i=1 Xi μ = 피[X] δ > 0 Pr[X ≥ (1 + δ)μ] ≤ ( eδ (1 + δ)(1+δ) ) μ
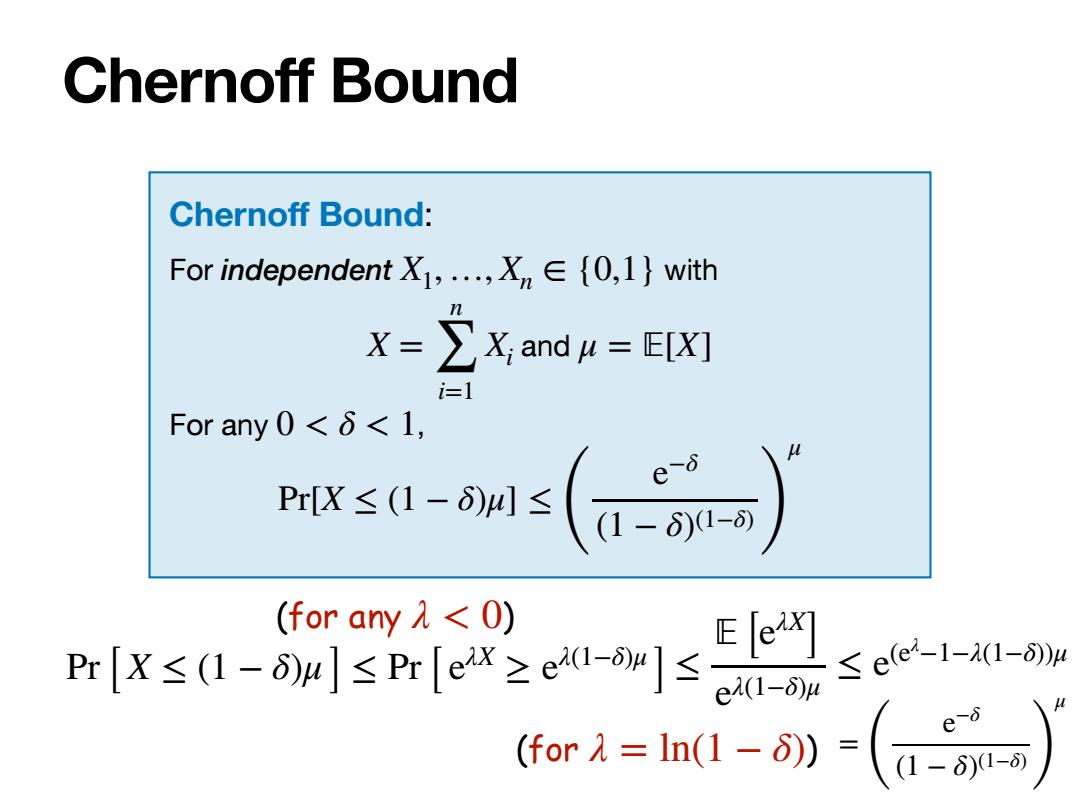
Chernoff Bound Chernoff Bound: For independent X1,,X,∈{0,l}with X-∑;and=E[X灯 i=1 For any0<δ<1, r-ms(as)》 tstlo (for any 0) ≤ee2-l-al-dw or=1n1-》-(a-)
Chernoff Bound: For independent with and For any , X1, …, Xn ∈ {0,1} X = n ∑ i=1 Xi μ = 피[X] 0 < δ < 1 Pr[X ≤ (1 − δ)μ] ≤ ( e−δ (1 − δ)(1−δ) ) μ Pr[ X ≤ (1 − δ)μ ] ≤ Pr[ eλX ≥ eλ(1−δ)μ ] (for any λ < 0) ≤ 피 [eλX ] eλ(1−δ)μ ≤ e(eλ −1−λ(1−δ))μ (for λ = ln(1 − δ)) = ( e−δ (1 − δ)(1−δ) ) μ Chernoff Bound
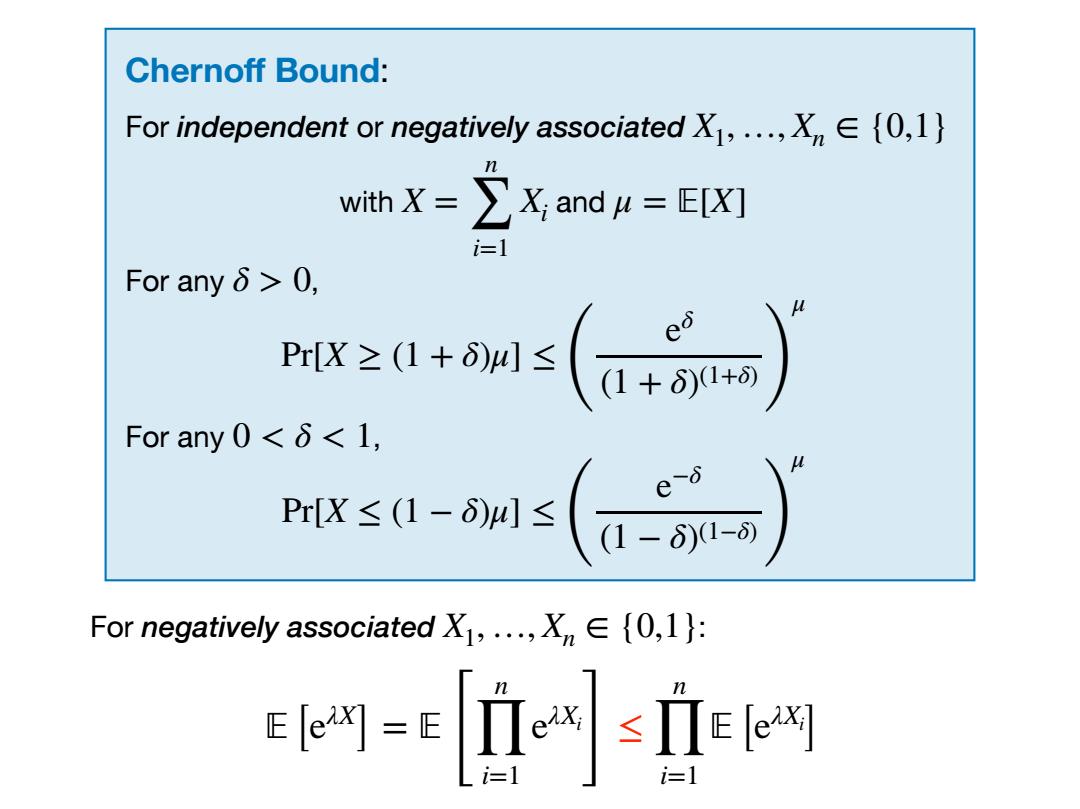
Chernoff Bound: For independent or negatively associated X1,...,XE(0,1} with=∑X;and=E[X] i=1 For anyδ>0, For any 0<<1, Pr[X≤(1-δ)川 ( For negatively associated X1,,Xn∈{0,l}: r-[i- i≥1
Chernoff Bound: For independent or negatively associated with and For any , For any , X1,…, Xn ∈ {0,1} X = n ∑ i=1 Xi μ = 피[X] δ > 0 Pr[X ≥ (1 + δ)μ] ≤ ( eδ (1 + δ)(1+δ) ) μ 0 < δ < 1 Pr[X ≤ (1 − δ)μ] ≤ ( e−δ (1 − δ)(1−δ) ) μ For negatively associated X : 1, …, Xn ∈ {0,1} 피 [eλX ] = 피 [ n ∏ i=1 eλXi ] ≤ n ∏ i=1 피 [eλXi ]
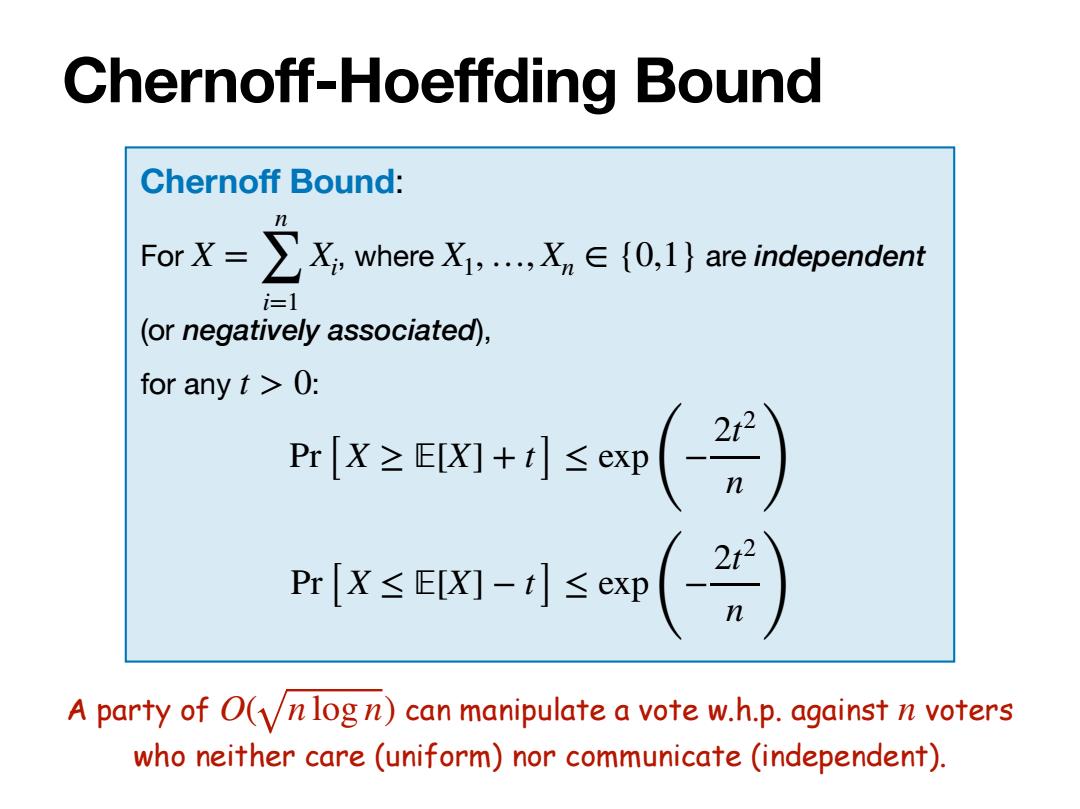
Chernoff-Hoeffding Bound Chernoff Bound: ForX=∑X,where Xi,,x,∈{0,I}areindependent i=1 (or negatively associated), for any t>0: Pr[X≥EX+]≤exp 的 Pr[X≤E[X灯-t≤exp A party of O(nlogn)can manipulate a vote w.h.p.against n voters who neither care(uniform)nor communicate (independent)
Chernoff-Hoeffding Bound Chernoff Bound: For , where are independent (or negatively associated), for any : X = n ∑ i=1 Xi X1, …, Xn ∈ {0,1} t > 0 Pr[ X ≥ 피[X] + t] ≤ exp (−2t 2 n ) Pr[ X ≤ 피[X] − t] ≤ exp (−2t 2 n ) A party of can manipulate a vote w.h.p. against voters who neither care (uniform) nor communicate (independent). O( n log n) n