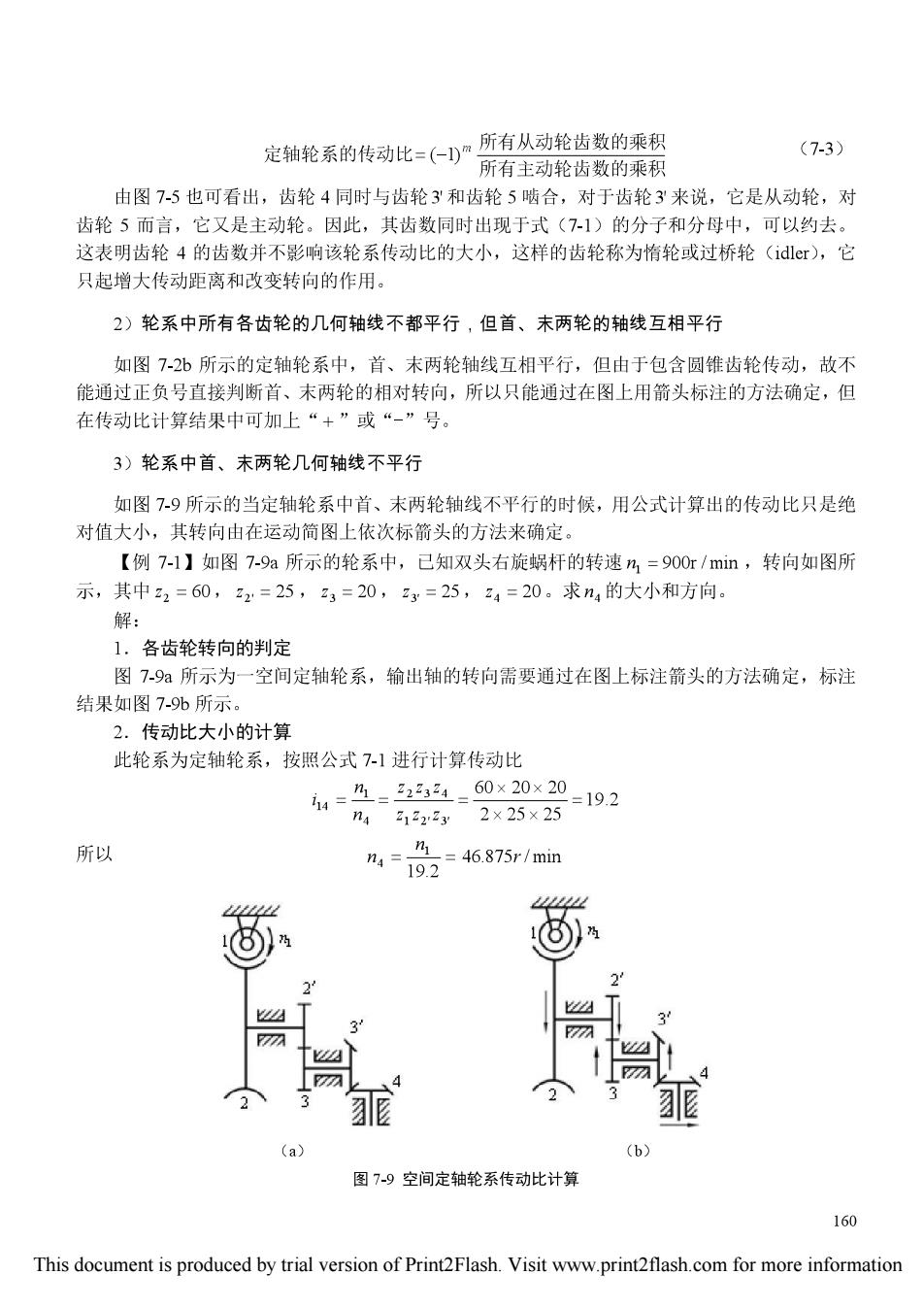
定轴轮系的传动比=(~1)”所有从动轮齿数的乘积 (7-3) 所有主动轮齿数的乘积 由图7-5也可看出,齿轮4同时与齿轮3'和齿轮5啮合,对于齿轮3'来说,它是从动轮,对 齿轮5而言,它又是主动轮。因此,其齿数同时出现于式(7-1)的分子和分母中,可以约去。 这表明齿轮4的齿数并不影响该轮系传动比的大小,这样的齿轮称为惰轮或过桥轮(idlr),它 只起增大传动距离和改变转向的作用。 2)轮系中所有各齿轮的几何轴线不都平行,但首、末两轮的轴线互相平行 如图7-2b所示的定轴轮系中,首、末两轮轴线互相平行,但由于包含圆锥齿轮传动,故不 能通过正负号直接判断首、末两轮的相对转向,所以只能通过在图上用箭头标注的方法确定,但 在传动比计算结果中可加上“+”或“-”号。 3)轮系中首、末两轮几何轴线不平行 如图79所示的当定轴轮系中首、末两轮轴线不平行的时候,用公式计算出的传动比只是绝 对值大小,其转向由在运动简图上依次标箭头的方法来确定。 【例7-1】如图7-9a所示的轮系中,已知双头右旋蜗杆的转速n=900r/min,转向如图所 示,其中22=60,z2=25,23=20,23=25,z4=20。求n4的大小和方向。 解: 1.各齿轮转向的判定 图7-9a所示为一空间定轴轮系,输出轴的转向需要通过在图上标注箭头的方法确定,标注 结果如图7-9b所示。 2.传动比大小的计算 此轮系为定轴轮系,按照公式7-1进行计算传动比 14=4=234=60×20x20 =19.2 n4212223y2×25×25 所以 1=46.875r/min 19.2 3 M 4 (a) (b 图7-9空间定轴轮系传动比计算 160 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

7.3周转轮系传动比 7.3.1周转轮系的组成 如图7-3所示,齿轮2既绕自身轴线O,回转,又随构件H绕O转动,它的运动像太阳系 中的行星运行一样,既有自转又有公转,故这种齿轮称为行星轮(planetary gear)。齿轮1和齿 轮3绕固定轴线转动,称为太阳轮(sun gear)。安装行星轮的可转动构件H称为行星架、转臂 或系杆(planet carrier)。一个系杆上的行星轮可以是一个也可以是多个。一个或多个相互啮合的 行星轮和安装这些行星轮的系杆,以及与这些行星轮相啮合的太阳轮就构成了一个周转轮系。周 转轮系的太阳轮与系杆的回转轴线必须共线,否则轮系不能运转。 由于太阳轮与系杆的回转轴均安装在机架上,便于运动和 动力的输入与输出,故周转轮系一般都以太阳轮和系杆作为运 动和动力输入或输出的构件,因此,它们称为周转轮系的基本 构件(basic link)。通常用K表示太阳轮,H表示系杆。 周转轮系可以按基本构件的不同进行分为2K-H型周转轮 系和3K型的周转轮系。如图7-3所示的周转轮系中由于有两个 太阳轮,则称为2KH型周转轮系;如图7-10所示的周转轮系 中由于有三个太阳轮,则称为3K型的周转轮系。在实际生产中, 应用最多的是2K-H型的周转轮系。 图7-103K型周转轮系 7.3.2周转轮系传动比的计算 由于周转轮系中不是所有的齿轮都做定轴转动,所以其传动比不能直接按照定轴轮系的传动 比来计算。要根据相对运动原理把它转化成定轴轮系再求其传动比。 如图7-11所示,若给整个周转轮系加上一个公共角速度“-①”,使之绕行星架的固定轴 线回转,这时各构件之间的相对运动仍将保持不变,而行星架的角速度变为-@⊙=0,这样 周转轮系就转化成了定轴轮系。这种采用反转法原理转化所成的定轴轮系称为原周转轮系的转化 轮系(inverted gear train)。转化轮系为定轴轮系,其传动比可以按照求定轴轮系传动比的方法来 求。于是可得该转化轮系中各个构件的角速度为 @f=a-au =02-0H o=03-0H @H-0 转化轮系的传动比 唱=-4里-3 am0,- 21 161 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information

其中“-”表示在转化轮系中轮@H与轮⊙的转向相反。上式包含了周转轮系中三个基本构件的 角速度与各齿轮数之间的关系。当已知@、⊙和@中任意两个角速度矢量的大小、方向和轮 系中各齿轮的齿数时,就可以确定出第三个角速度矢量的大小和方向,从而可以进一步求出任意 两个基本构件之间的传动比。 根据上述原理,可以得出周转轮系传动比的一般关系式。设周转轮系中的两个太阳轮分别为 m和n,行星架为H,则其转化轮系的传动比为 点-唱-- @n-Wd (7-4) =士转化轮系转化齿轮m至齿轮n间各从动轮齿数的乘积 转化轮系转化齿轮m至齿轮n间各主动轮齿数的乘积 af =a;-wg =一红 2 (a) (b) (c) 图7-11周转轮系的转化 特别注意: (1)公式中的“+”、“-”号与两太阳轮的真实转向无关,即“+”号,并不表示两太阳轮 的真实转向一定相同,“-”号也并不表示两太阳轮的真实转向一定相反,它仅表示在转化轮系中, 两个构件m、n的相对运动关系,可以称为是周转轮系的“结构特征”符号。 (2)品≠1m,品为转化轮系中轮m和轮n的转速之比,其大小和正负号由定轴轮系传 动比计算方法确定;而则是周转轮系中轮m和轮n的转速之比,其大小和正负号必须由计算结 果确定。 (3)公式中的①m、@,和必须为平行矢量时才能进行代数相加减,也就是说必须是轴 线相互平行或重合的齿轮、系杆的角速度。 (4)将①m、⊙和®的己知量代入公式进行计算时,必须代入正负号。所以在计算前往 往应先假定某一方向的转速为正,则其他转速与其相同者为正,反之为负。 若所研究的轮系为具有固定轮的行星轮系,设固定轮为n,则®。=0,则可得 162 This document is produced by trial version of Print2Flash.Visit www.print2flash.com for more information
This document is produced by trial version of Print2Flash. Visit www.print2flash.com for more information