
5.3理想气体压强和温度公式 5.3理想气体压强和温度公式 一理想气体的微观模型 (1)忽略分子体积。 (②)分子运动服从牛顿运动定律。 (3)除碰撞外,没有相互作用。 分子统计假设 1)速度各不相同,由于碰撞而变化。 2)平衡态时,数密度分布均匀。 3)平衡态时,速度沿各方向分布均匀。 前页后页目录 1
前页 后页 目录 1 5.3 理想气体压强和温度公式 一. 理想气体的微观模型 (1) 忽略分子体积。 (2) 分子运动服从牛顿运动定律。 (3) 除碰撞外,没有相互作用。 分子统计假设 1) 速度各不相同,由于碰撞而变化。 2) 平衡态时,数密度分布均匀。 3) 平衡态时,速度沿各方向分布均匀。 5.3 理想气体压强和温度公式

5,3理想气体压强和温度公式 N Vx Ux= i=l =0 i=1 -≠0 N 0x=0y=02=0 -= N ∑(++) 2 i=l N =++ 3 前页后页目录 2
前页 后页 目录 2 5.3 理想气体压强和温度公式 1 0 = = = N ix i x N v v = = = 0 v v v x y z 2 2 1 0 = = N ix i x N v v 2 2 2 v v v x y z = = 2 2 =1 = N i i N v v 2 2 2 2 v v v v = + + x y z 2 2 1 3 v v x = 2 2 2 =1 + + = ( ) N ix iy iz i N v v v
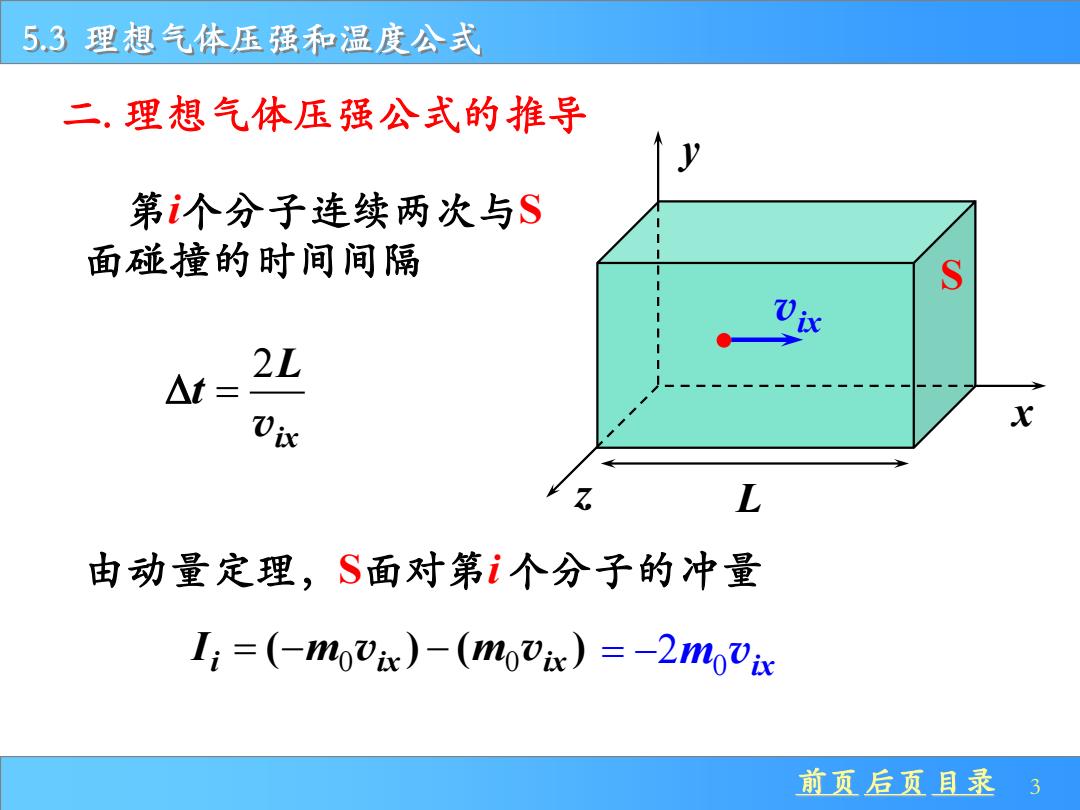
5.3理想气体压强和温度公式 二,理想气体压强公式的推导 第i个分子连续两次与S 面碰撞的时间间隔 S 0 At= 2L Vix 由动量定理,S面对第i个分子的冲量 Ii=(-movix)-(movix)=-2m0vix 前页后页目录3
前页 后页 目录 3 5.3 理想气体压强和温度公式 二. 理想气体压强公式的推导 x y z vix S L 第i个分子连续两次与S 面碰撞的时间间隔 2 = ix L t v 由动量定理,S面对第i个分子的冲量 = − − 0 0 ( ) ( ) i ix ix I m m v v 0 = −2m vix

5.3理想气体压强和温度公式 第i个分子对S面的冲量 I=-Ii=2m0vix 第i个分子对S面的平均冲力 29=m0元 △t 2L1Vix L S面所受平均力 L 前页后页目录4
前页 后页 目录 4 5.3 理想气体压强和温度公式 第i 个分子对S面的冲量 I I i i = − 第i 个分子对S面的平均冲力 = i i I F t 0 2 2 = / ix ix m L v v 2 0 = m ix L v S面所受平均力 =1 = N i i F F 2 0 =1 = N ix i m L v 0 = 2m vix

5,3理想气体压强和温度公式 S面上气体压强 mo i=l S台SLV N 21 =nmoV=。nmo)1 3 分子平均平动动能 11 %a2 21 6kt= N台2 movi= 2 理想气体的压强 2,1 2 p=3吃m,0) p=n6kt 前页后页目录 5
前页 后页 目录 5 5.3 理想气体压强和温度公式 S面上气体压强 = F p S 2 0 =1 = N ix i m SL v 2 1 0 N ix N m i V N = = v 2 = nm0vx 2 0 1 3 = nm v 分子平均平动动能 2 0 1 2 = m v 理想气体的压强 2 0 2 1 3 2 p n m = ( ) v 2 3 = kt p n 2 0 1 1 1 2 kt N i i m N = = v