
4.4狭义相对论动力学基础 4.4狭义相对论动力学基础 一.相对论力学的基本方程 1.动量p= 2.相对论力学的基本方程 F= p _d(m) F≠md dt dt 3.质量 mo m= m0一静止质量 质量是相对的, 理论 静止质量最小。 推导 前页后页目录
前页 后页 目录 1 4.4 狭义相对论动力学基础 1.动量 p m= v 3.质量 0 2 2 1 m m c v = − m0—静止质量 2.相对论力学的基本方程 d d p F t = 一. 相对论力学的基本方程 4.4 狭义相对论动力学基础 F ma 质量是相对的, 静止质量最小。 d( ) d m t v = 理论 推导

4.4狭义相对论动力学基础 mo d(mi) m= F- 711 dt dt 1- 火箭w=11.2km/s,m=1.0000000009m 电子)=0.98c,m=5mo 讨论: 1)当<<c时,m→。回到牛顿力学。 2)当v→C时,m→oo。极限速度c。 3)当v=c时,mo=0。光子 前页后页目录2
前页 后页 目录 2 4.4 狭义相对论动力学基础 0 2 2 1 m m c v = − d d( ) d d p m F t t v = = 讨论: 1)当v<< c 时,m → m0 。回到牛顿力学。 2)当v → c 时,m → 。极限速度c。 3)当v = c 时,m0 = 0。光子 火箭v =11.2km/s,m=1.000 000 000 9m0 电子v =0.98c,m=5m0

4.4狭义相对论动力学基础 二.质量和能量的关系 1.相对论动能 Ey me2-moc2 ds Fds dEk dt Fdt dp Ek=∫dEk=∫odp=op-∫pdo e mo”=dw 前页后页目录3
前页 后页 目录 3 4.4 狭义相对论动力学基础 1.相对论动能 2 2 E mc m c k = − 0 二. 质量和能量的关系 d d s t v = d d F s F t = d k d E p = E E k k = d = vdp = − v v p pd 2 0 2 2 1 / m c v v = − 2 0 2 0 2 2 1 / m c m c v c = − − 0 0 2 2 1 d / m c v v v v − −
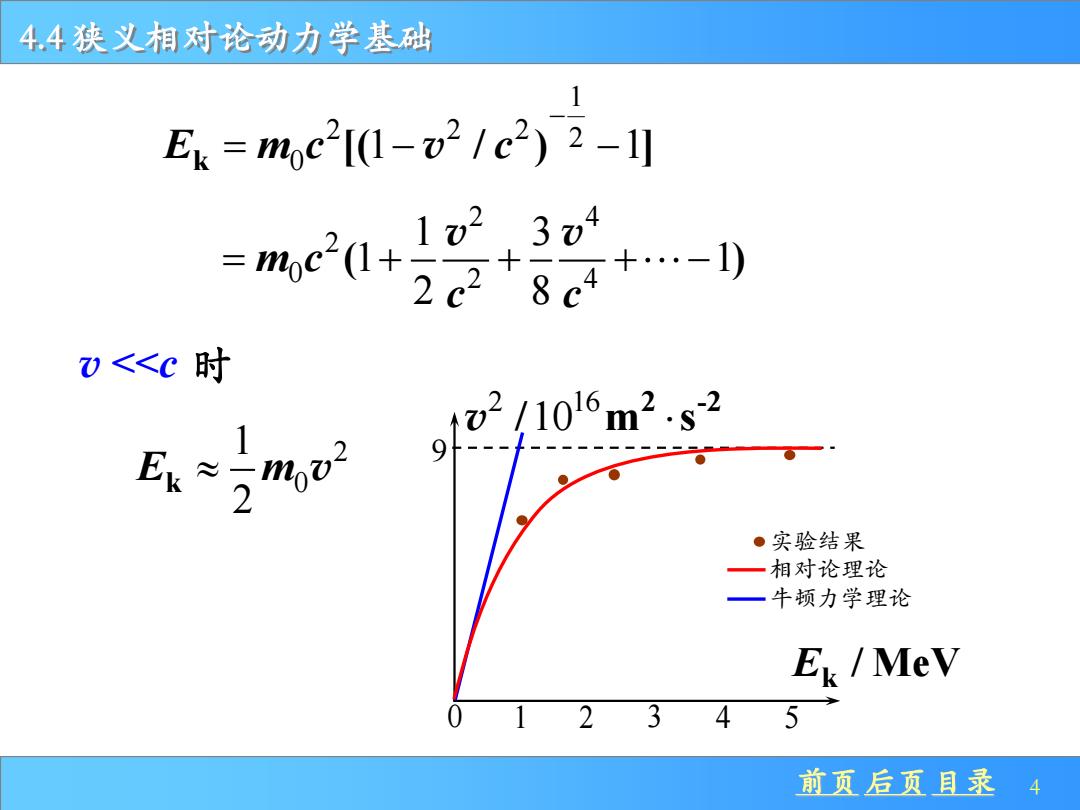
4.4狭义相对论动力学基础 Ek=mc2I1-21c2)2-l川 v<<c时 2/1016m2.s2 ●实验结果 一相对论理论 一牛顿力学理论 EL/MeV 12345 前页后页目录4
前页 后页 目录 4 4.4 狭义相对论动力学基础 v <<c 时 实验结果 相对论理论 牛顿力学理论 k E / MeV 2 16 10 2 -2 v / m s 9 0 1 2 3 4 5 2 4 2 0 2 4 1 3 1 1 2 8 m c ( ) c c v v = + + + − 1 2 2 2 2 0 1 1 k E m c c [( / ) ] v − = − − 2 0 1 2 E m k v

4.4狭义相对论动力学基础 Ek mc2-moc2 2.相对论能量E=mc2 质能关系 3.静能 Eo=moc2 能量守恒 ∑E,-∑m,c2=常量 质量守恒∑m:=常量 前页后页目录5
前页 后页 目录 5 4.4 狭义相对论动力学基础 2 2 E mc m c k = − 0 3.静能 2 E m c 0 0 = 2.相对论能量 2 E mc = 质能关系 能量守恒 2 i i i i E m c = =常量 质量守恒 i i m =常量