
4.3狭义相对论时空观 4.3狭义相对论时空观 假想实验 火车参考系 ■>4II 一.同时的相对性 两个异地事件在一惯性系中是同时的,在另 一惯性系中是不同时的。 前页后页目录1
前页 后页 目录 1 4.3 狭义相对论时空观 一. 同时的相对性 两个异地事件在一惯性系中是同时的,在另 一惯性系中是不同时的。 假 想 实 验 4.3 狭义相对论时空观

4.3狭义相对论时空观 洛伦兹变换→导出同时的相对性 设K系中两个事件的时空坐标分别为A(x1,0,0,)和 B(心2,0,0,2),在K'系中两个事件的时空坐标分别为 A(K'1,0,0,t1)和B(x'20,0,t2),由洛伦兹逆变换 巧+2 4=-w21c2 t,=-w21c (6-)+3(-) t2-t1= 同时是相对的 V1-v21c2 前页后页目录2
前页 后页 目录 2 4.3 狭义相对论时空观 洛伦兹变换→导出同时的相对性 设K系中两个事件的时空坐标分别为A(x1 ,0,0,t1 )和 B(x2 ,0,0,t2 ),在K系中两个事件的时空坐标分别为 A(x 1 ,0,0,t 1 )和B(x 2 ,0,0,t 2 ) ,由洛伦兹逆变换 1 1 2 1 2 2 1 / t x c t c + = − v v 2 2 2 2 2 2 1 / t x c t c + = − v v 2 1 2 1 2 2 1 2 2 1 ( ) ( ) / x x c t t t t c − − + − − = v v 同时是相对的
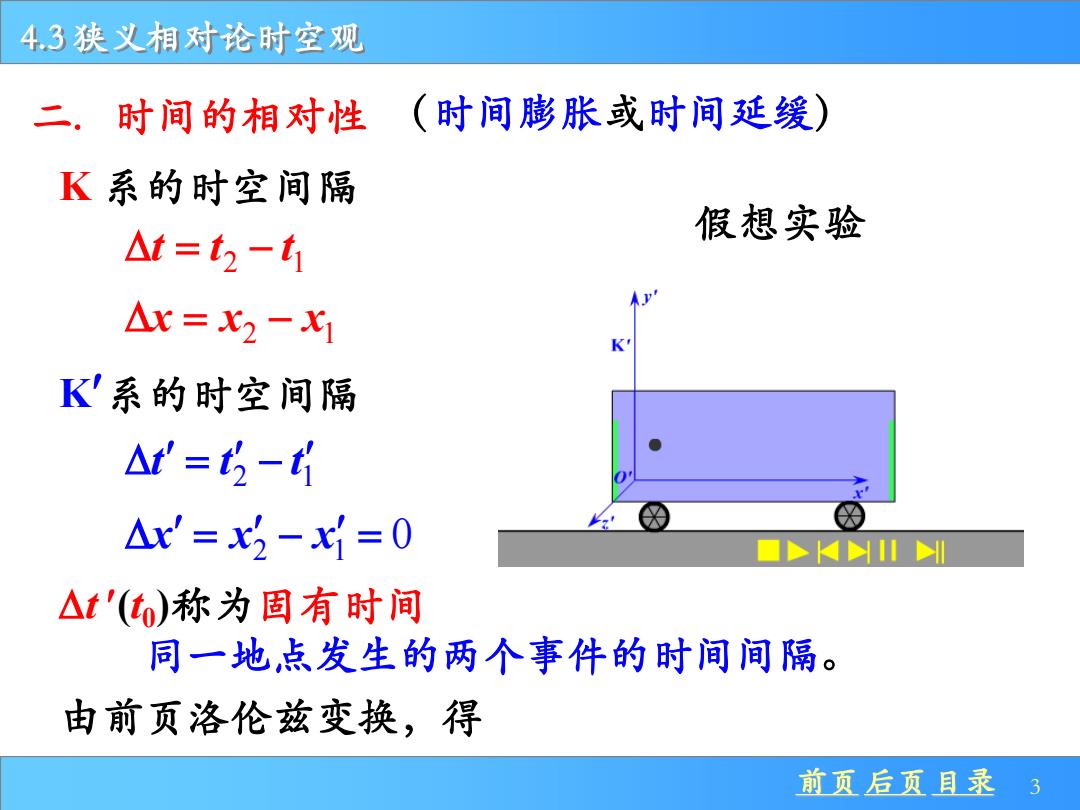
4.3狭义相对论时空观 二.时间的相对性 (时间膨胀或时间延缓) K系的时空间隔 假想实验 △t=t2-t1 △x=X2-X1 K'系的时空间隔 △t=t5- △x'=x2-x=0 △t'(t)称为固有时间 同一地,点发生的两个事件的时间间隔。 由前页洛伦兹变换,得 前页后页目录3
前页 后页 目录 3 4.3 狭义相对论时空观 二. 时间的相对性 K 系的时空间隔 2 1 = − t t t 2 1 = − x x x K系的时空间隔 2 1 = − t t t 2 1 = − = x x x 0 t (t0 )称为固有时间 同一地点发生的两个事件的时间间隔。 假想实验 由前页洛伦兹变换,得 (时间膨胀或时间延缓)

43狭义相对论时空观 △t △t 或t= to 假想实验二 狭义相对论中,时间(间隔)是相对的。 固有时间最短。 在运动参照系中时间变大,称为时间膨胀效 应,或动钟变慢。 时间膨胀效应”被粒子物理实验所证实。 时间膨胀效应”是相对论的时空效应,与 钟的具体结构和其他外界因素无关。 前页后页目录4
前页 后页 目录 4 4.3 狭义相对论时空观 2 2 1 t t c = − v 狭义相对论中,时间(间隔)是相对的。 固有时间最短。 在运动参照系中时间变大,称为时间膨胀效 应,或动钟变慢。 “时间膨胀效应”被粒子物理实验所证实。 “时间膨胀效应” 是相对论的时空效应,与 钟的具体结构和其他外界因素无关。0 2 2 1 t t c = − v 或 假 想 实 验 二

4.3狭义相对论时空观 动钟变慢是相对的 慢 慢 ←一0 前页后页目录5
前页 后页 目录 5 4.3 狭义相对论时空观 v 动钟变慢是相对的 慢 v 慢