
式中:入为固体在温度T时的热导率;ko,k为经验常数。一般,金属材料,k<0;非金属材料,k>0。即,金属,非金属。(2)液体和气体的热导率一般T,入,入。。(水和甘油除外)2.2通过单层壁的稳定热传导2.2.1单层平壁的稳定热传导温度仅沿x方向变化,导热为一维热传导。由傅立叶定律可写出:dxq=- 入dT/dx若材料的热导率为常量,积分上式可得:q=入(Ti-T2)/b
式中:λ为固体在温度T时的热导率;k0,k 为经验常数。一般,金属材料,k<0;非金 属材料,k>0。 即 T↑,λ金属↓,λ非金属↑。 (2)液体和气体的热导率 一般T↑,λL↓,λg↑。 (水和甘油除外) 2.2 通过单层壁的稳定热传导 2.2.1 单层平壁的稳定热传导 温度仅沿 x 方向变化,导热为一维热传导。 由傅立叶定律可写出: q=-λdT/dx 若材料的热导率为常量,积分上式可得: q=λ(T1-T2)/b

=--或bR元Q=asl-或b式中,R=b/入,导热热阻,m·℃/W工程计算中,热导率可取两壁面温度下入值的算术平均值,或取两壁面温度之算术平均值下的入值。温度分布:当入为常量时,由于q=入(Ti-T,)/b=入(Ti-T)/x故平壁内任一等温面的温度为T=Ti-(Ti-T2) x/b显然,入为常量时,单层平壁内的温度分布为直线。2.2.2单层圆筒壁的热传导
或 R T b TT q Δ = − = λ 21 或 b TT SQ − 21 = λ 式中,R=b/λ,导热热阻,m2 •℃/W 工程计算中,热导率可取两壁面温度下λ值 的算术平均值,或取两壁面温度之算术平均 值下的λ值。 温度分布: 当λ为常量时,由于 q=λ(T1-T2)/b=λ(T1-T)/x 故平壁内任一等温面的温度为 T=T1-(T1-T2)x/b 显然,λ为常量时,单层平壁内的温度分布 为直线。 2.2.2 单层圆筒壁的热传导
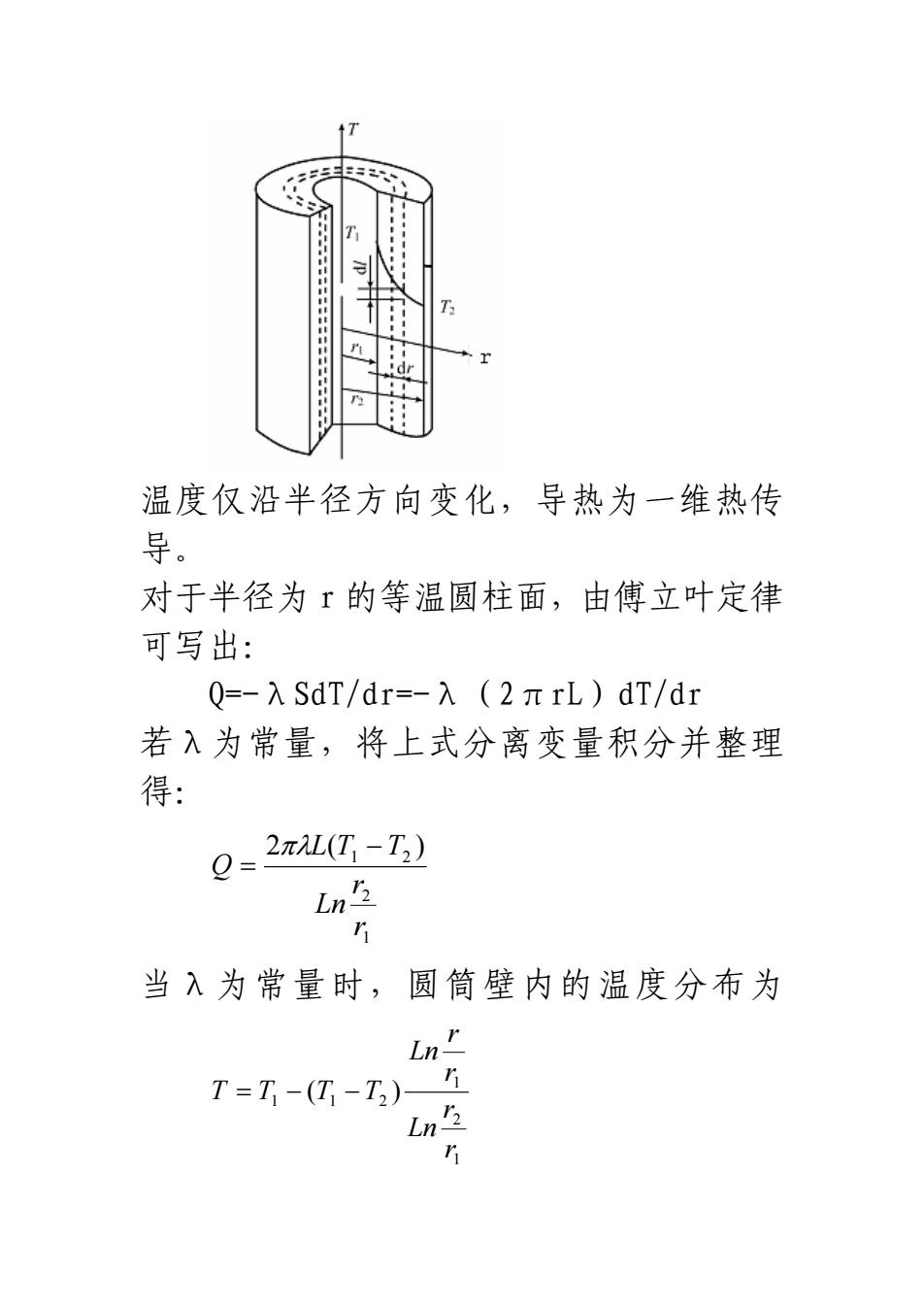
温度仅沿半径方向变化,导热为一维热传导。对于半径为r的等温圆柱面,由傅立叶定律可写出:Q=-入 SdT/dr=-入(2πrL)dT/dr若入为常量,将上式分离变量积分并整理得:2元(T, -T,)Q=1Ln2T当入为常量时,圆筒壁内的温度分布为Ln=AT = T -(T - T,)-Ln'2G
温度仅沿半径方向变化,导热为一维热传 导。 对于半径为 r 的等温圆柱面,由傅立叶定律 可写出: Q=-λSdT/dr=-λ(2πrL)dT/dr 若λ为常量,将上式分离变量积分并整理 得: 1 2 21 )(2 r r Ln TTL Q − = πλ 当λ为常量时,圆筒壁内的温度分布为 1 2 1 211 )( r r Ln r r Ln −−= TTTT
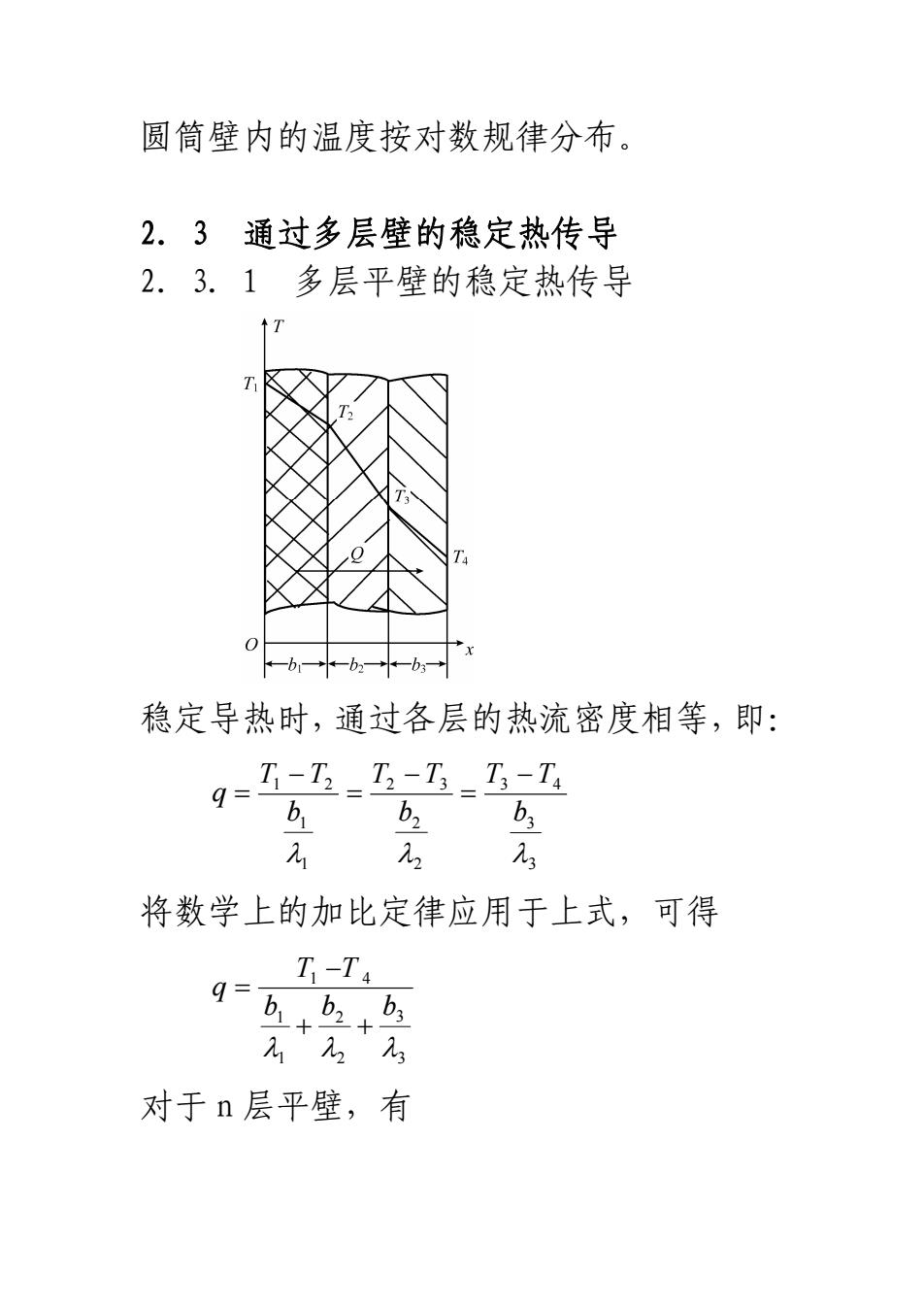
圆筒壁内的温度按对数规律分布。2.3通过多层壁的稳定热传导2.3.1多层平壁的稳定热传导稳定导热时,通过各层的热流密度相等,即:T-T_-T_T-Tq=bbb2将数学上的加比定律应用于上式,可得T, T 4q=bitb+be对于n层平壁,有
圆筒壁内的温度按对数规律分布。 2.3 通过多层壁的稳定热传导 2.3.1 多层平壁的稳定热传导 稳定导热时,通过各层的热流密度相等,即: 3 3 43 2 2 32 1 1 21 λλ λ b TT b TT b TT q − = − = − = 将数学上的加比定律应用于上式,可得 3 3 2 2 1 1 41 λλλ bb b TT q ++ − = 对于 n 层平壁,有
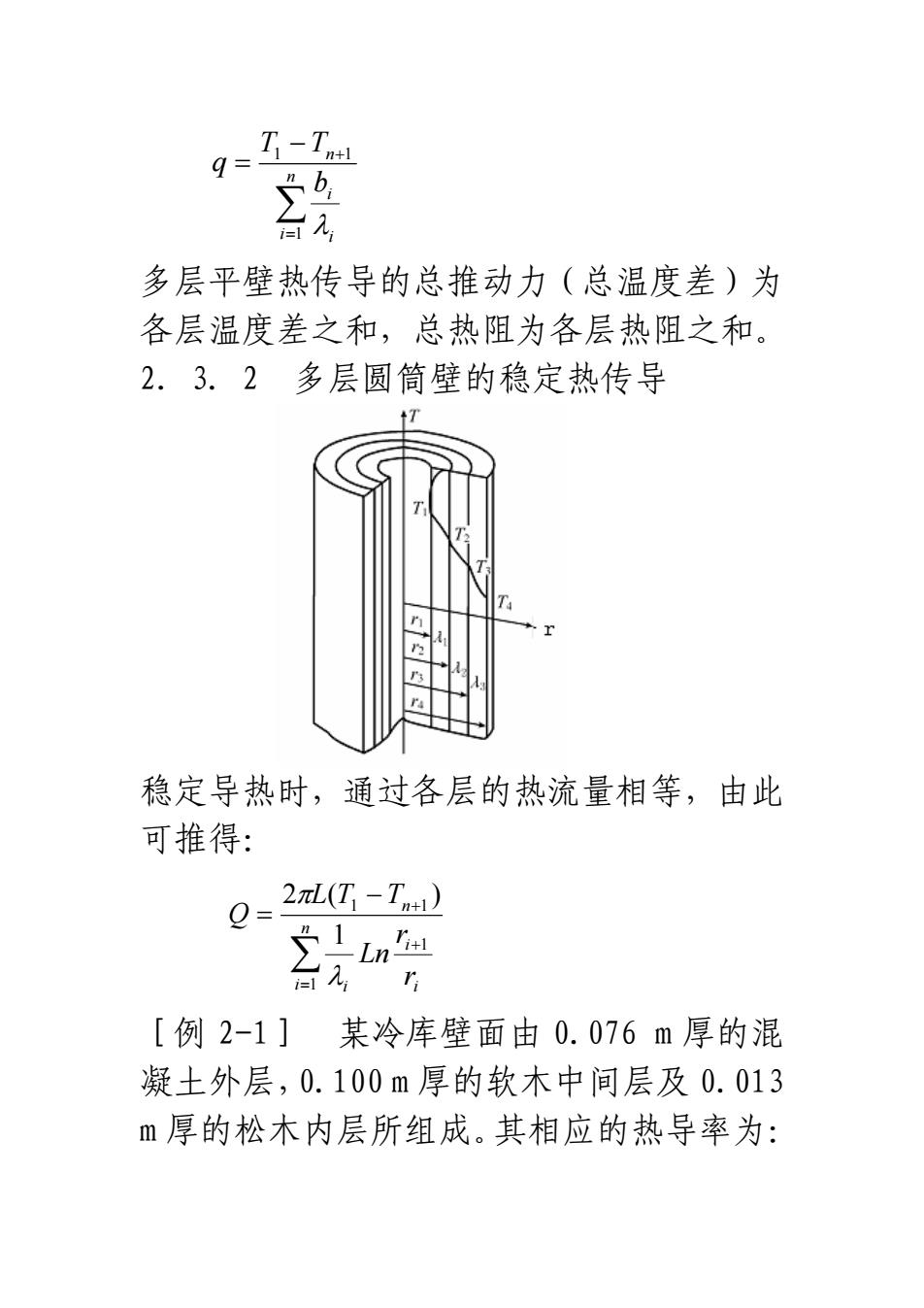
T - Th+17多层平壁热传导的总推动力(总温度差)为各层温度差之和,总热阻为各层热阻之和。2.3.2多层圆筒壁的稳定热传导稳定导热时,通过各层的热流量相等,由此可推得:α= 2ml(T -Tm)ZTLn台[例2-1]某冷库壁面由0.076m厚的混凝土外层,0.100m厚的软木中间层及0.013m厚的松木内层所组成。其相应的热导率为:
∑= − + = n i i i n b TT q 1 11 λ 多层平壁热传导的总推动力(总温度差)为 各层温度差之和,总热阻为各层热阻之和。 2.3.2 多层圆筒壁的稳定热传导 稳定导热时,通过各层的热流量相等,由此 可推得: ∑= + − + = n i i i i n r r Ln TTL Q 1 1 11 1 )(2 λ π [例 2-1] 某冷库壁面由 0.076 m 厚的混 凝土外层,0.100 m 厚的软木中间层及 0.013 m 厚的松木内层所组成。其相应的热导率为: