
例题 §5.3相律 (1)、冰水共存 C=1,Φ=2 (冰、水),f=1-2+2=1(T或p) (2)、NH,CI(s)部分分解为NH(g)和HCl(g) S=3,R=1,R'=1,D=2NH,CI固相、气相) f=3-1-1-2+2=1 (T、p,xNB或xa其中之一) (3)1000K下,NH3、H2、N2三气平衡 S=3,R=1(2NH33H2+N2),Φ=1 ∫=CD+1=2p、xB、xm或x2其中之二)
§ 5.3 相律 C=1, =2 (冰、水), f = 1-2+2=1 (T或p) (2)、NH4Cl(s)部分分解为NH3 (g)和HCl(g) S=3,R=1,R’=1, =2 (NH4Cl固相、气相) f = 3 – 1 – 1 – 2 + 2 = 1 (T、p、 x NH3或xHCl其中之一) (3) 1000K下,NH3、H2、N2三气平衡 S=3,R=1 (2NH3 =3H2+N2 ), =1 f = C- +1=2 (p、xNH3、x H2或x N2其中之二) (1)、冰水共存 例题

4.相律的几点说明 §5.3相律 一般情况下,只考虑温度T和压力p这两个 因素时,式中的n=2,于是相律为 f=C-Φ+2 若指定了温度或压力,则 f*=C-Φ+1 f*一条件自由度; 若温度和压力同时固定,则 **=C-
§ 5.3 相律 一般情况下,只考虑温度T和压力p这两个 因素时,式中的n=2,于是相律为 f =C- +2 若指定了温度或压力,则 f * =C- +1 f *—条件自由度; 若温度和压力同时固定,则 f ** = C- 4. 相律的几点说明

5.相律的意义 多组分多相系统是十分复杂的,但借 助相律可以确定研究的方向。相律表明了 相平衡系统中有几个独立变量,当独立变 量选定了之后,相律还表明其他的变量必 为这几个独立变量的函数(但是相律不能 告诉我们这些函数的具体形式)
5. 相律的意义 多组分多相系统是十分复杂的,但借 助相律可以确定研究的方向。相律表明了 相平衡系统中有几个独立变量,当独立变 量选定了之后,相律还表明其他的变量必 为这几个独立变量的函数(但是相律不能 告诉我们这些函数的具体形式)

§5.4单组分体系的相平衡 单组分体系的相数与自由度 C=1 f+F=C+2=3 当 F=1 单相 f=2 双变量体系 F=2 两相平衡衡 f=1 单变量体系 P=f (T)- 克-克方程☆ F=3 三相共存 f=0 无变量体系 Dmax=3,∫max=2,双变量体系的相图可用平面图表示
§ 5.4 单组分体系的相平衡 C =1 f C + = + = F 2 3 当 F =1 单相 f = 2 双变量体系 F = 2 两相平衡 f =1 单变量体系 F = 3 三相共存 f = 0 无变量体系 max=3, f max=2,双变量体系的相图可用平面图表示。 单组分体系的相数与自由度 p=f(T)— 克-克方程
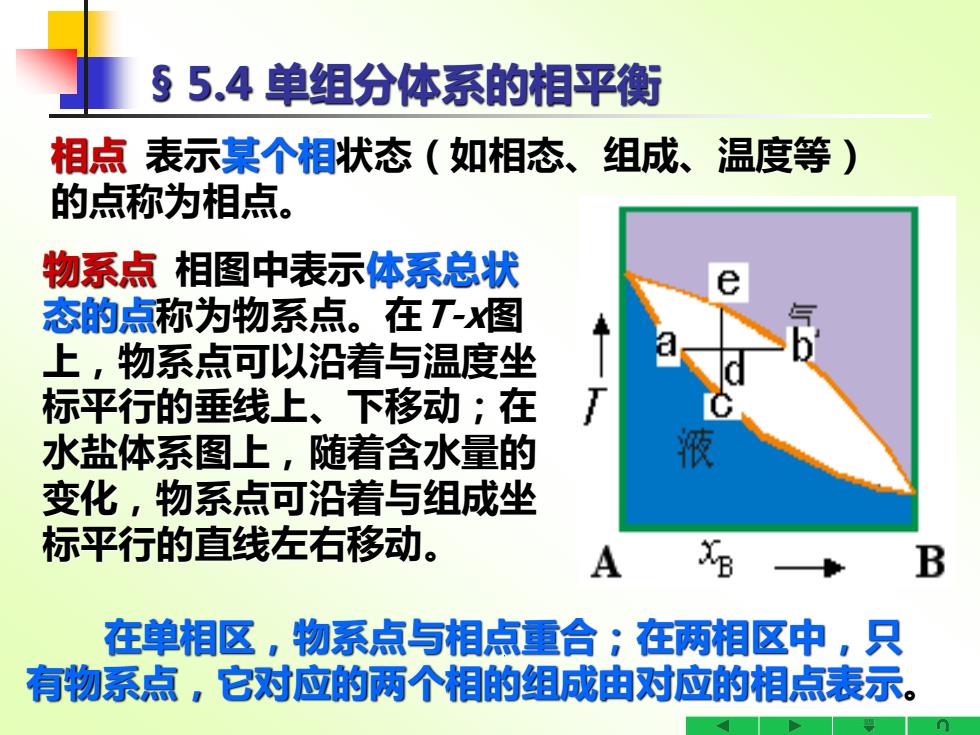
§5.4单组分体系的相平衡 相点表示某个相状态(如相态、组成、温度等) 的点称为相点。 物系点相图中表示体系总状 态的点称为物系点。在T-图 上,物系点可以沿着与温度坐 标平行的垂线上、下移动;在 水盐体系图上,随着含水量的 液 变化,物系点可沿着与组成坐 标平行的直线左右移动。 A B 在单相区,物系点与相点重合;在两相区中,只 有物系点,它对应的两个相的组成由对应的相点表示
§ 5.4 单组分体系的相平衡 相点 表示某个相状态(如相态、组成、温度等) 的点称为相点。 物系点 相图中表示体系总状 态的点称为物系点。在T-x图 上,物系点可以沿着与温度坐 标平行的垂线上、下移动;在 水盐体系图上,随着含水量的 变化,物系点可沿着与组成坐 标平行的直线左右移动。 在单相区,物系点与相点重合;在两相区中,只 有物系点,它对应的两个相的组成由对应的相点表示