Cutset retiming /966 (1) (1) 1 D D 0 (1) (2) 2D (1) (2) 3D 2 3 2 3 D (② (2) 4 4 r(1)=0,r(2)=1,r(3)=0,r(4)=1 -】 min{w(e)}≤k≤min{w(e)} G1→G2 G3→G1 k=1 2021年2月 11
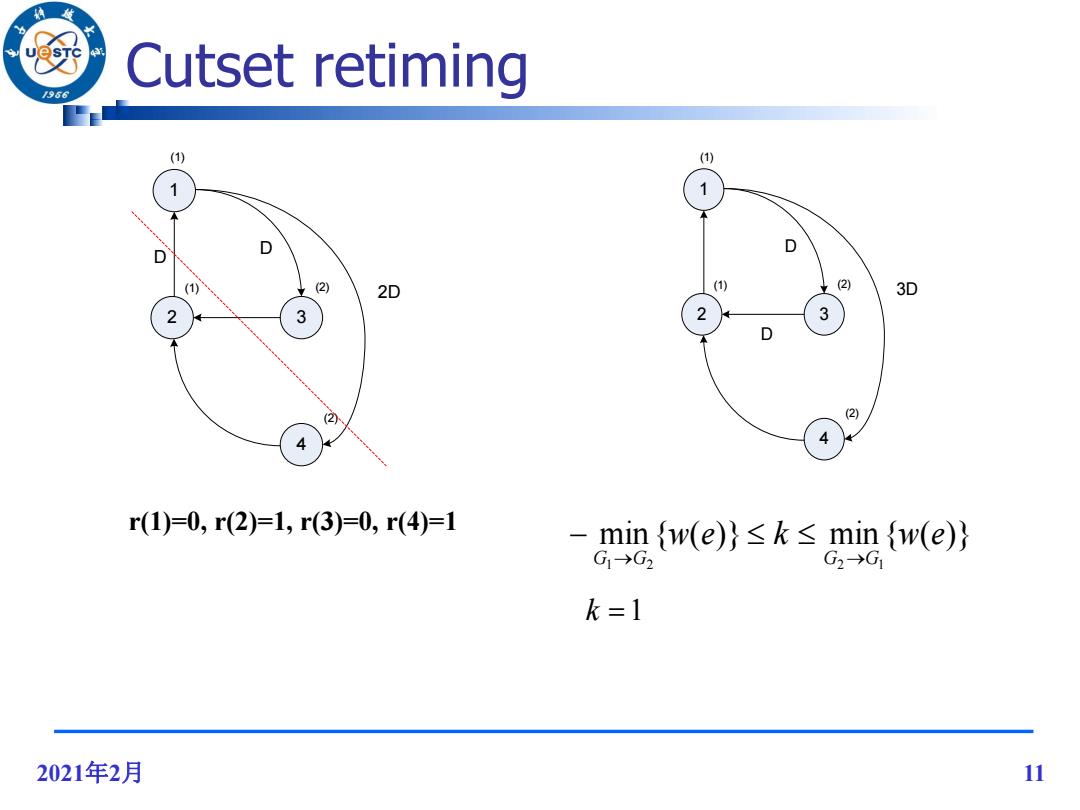
2021年2月 11 Cutset retiming 1 4 2 3 D D 3D (1) (1) (2) (2) k 1 1 4 2 3 D D 2D (1) (1) (2) (2) min { ( )} min { ( )} 1 2 2 1 w e k w e G G G G r(1)=0, r(2)=1, r(3)=0, r(4)=1
Cutset retiming /966 (1) () 1 D D (1) (2) 2D (1) (2) 2D 2 3 2 3 D 0 2四 四 Special case: min{w(e)}≤k≤min{w(e)} r(1)=0,r(2)=1,r(3)=0,r(4)=0 G1→G2 G2→G1 k=1 2021年2月 12
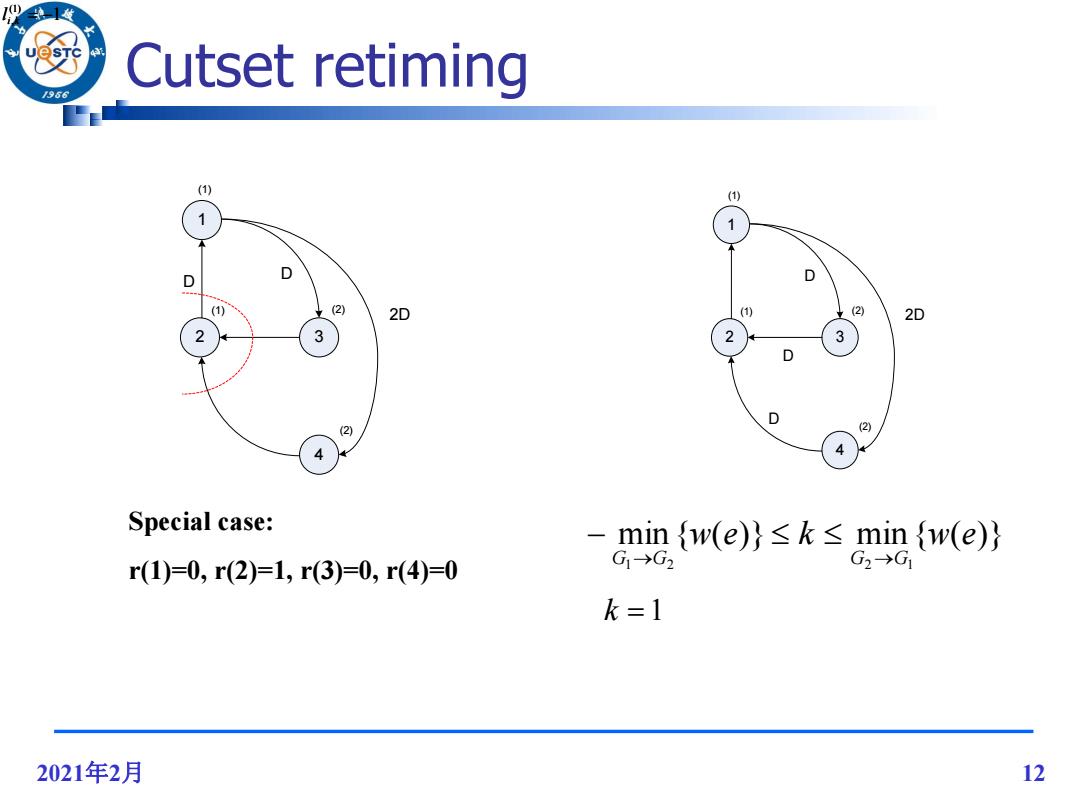
2021年2月 12 Cutset retiming 1 4 2 3 D D 2D (1) (1) (2) (2) 1 (1) l i,k 1 (1) l i,k 1 4 2 3 D D 2D (1) (1) (2) (2) D k 1 min { ( )} min { ( )} 1 2 2 1 w e k w e G G G G Special case: r(1)=0, r(2)=1, r(3)=0, r(4)=0

Pipelining /96 Pipelining is a special case of cutset retiming where there are no edges in the cutset from subgraph G2 to GL These cutset are referred to as feed forward cutsets. All of the edges in the cutset go from G to G2,and performing cutset retiming with k results in k additional delays on each in the cutset. x(n) x(n) D D b0 b b2 b0 b b2 y(n) D y(n) 2021年2月 13
2021年2月 13 Pipelining Pipelining is a special case of cutset retiming where there are no edges in the cutset from subgraph G2 to G1 . These cutset are referred to as feed forward cutsets. All of the edges in the cutset go from G1 to G2 , and performing cutset retiming with k results in k additional delays on each in the cutset. D D X X X + + x(n) y(n) b0 b1 b2 D D X X X + + x(n) y(n) b0 b1 b2 D D D