
一、课程的地位与作用 《专业的认识与实践》是信息与计算科学专业的重要课程之一,通过本课程的学习,使 学生了解信息与计算科学专业的内涵、专业发展现状、专业优势与特色,以及未来的就业发 展情况:为学生如何制定四年规划以及确定如何进行选课、就业考研以及设定未来发展的目 标起着很大的指导作用,且能锻炼学生自主学习和分析问题的能力。 二、课程对应的毕业要求 通过该课程的学习使学生充分认识到自己的专业,通过该课程学习,针对复杂工程问题, 能够理解和评价工程实际对自然环境、社会环境以及可持续发展的影响。培养具有自主学习 和终身学习的意识,有不断学习和适应发展的能力。 三、课程教学目标 通过本课程的学习,使学生了解信息与计算科学专业的内涵,了解我校信息与计算科学 专业的发展史、发展现状、就业与考研、社会定位:掌握培养方案中的课程设置模块,了解 四年的开课机会,每门课程的基本内容与在专业设置中的地位:为大学生制定四年规划和设 定未来发展目标起着很大的指导作用。通过实践学习锻炼学生自主学习的能力。 四、课程教学内容提要与基本要求 实践部分 序号 教学内容提要 基木要求 学时 了解信息与计算科学专业的内函:了解我校信息与 计算科学专业的发展现状、专业优势与特色、专业 1 专业基本情况介绍 发展潜力。介绍培养方案与课程设置。当前专业发 展热占第, 2 数学类专业课程介绍 计算机类课程介绍 了解每学期计算机类课程的设置与地位:了解每门 课程的基本内容与作用。 过与代往屈生的流。认口到信业的热 经验交流与大学四年规划 特色 对专业未来的发展充满信 大学四年规划 设想进行PPT答辩 五、说明 本课程与其他课程的关系 通过本课程的学习,学生掌握了课程模块的设置,为后期的专业课程选课打下坚实的基 础。 六、学生成绩考核与评定方式 本课程考核方式为答辩,成绩由平时成绩和答辩成绩两部分构成,其中平时成绩占30%, 答舞成绩占70%
11 一、课程的地位与作用 《专业的认识与实践》是信息与计算科学专业的重要课程之一,通过本课程的学习,使 学生了解信息与计算科学专业的内涵、专业发展现状、专业优势与特色,以及未来的就业发 展情况;为学生如何制定四年规划以及确定如何进行选课、就业考研以及设定未来发展的目 标起着很大的指导作用,且能锻炼学生自主学习和分析问题的能力。 二、课程对应的毕业要求 通过该课程的学习使学生充分认识到自己的专业,通过该课程学习,针对复杂工程问题, 能够理解和评价工程实际对自然环境、社会环境以及可持续发展的影响。培养具有自主学习 和终身学习的意识,有不断学习和适应发展的能力。 三、课程教学目标 通过本课程的学习,使学生了解信息与计算科学专业的内涵,了解我校信息与计算科学 专业的发展史、发展现状、就业与考研、社会定位;掌握培养方案中的课程设置模块,了解 四年的开课机会,每门课程的基本内容与在专业设置中的地位;为大学生制定四年规划和设 定未来发展目标起着很大的指导作用。通过实践学习锻炼学生自主学习的能力。 四、课程教学内容提要与基本要求 实践部分 序号 教学内容提要 基本要求 学时 1 专业基本情况介绍 了解信息与计算科学专业的内涵;了解我校信息与 计算科学专业的发展现状、专业优势与特色、专业 发展潜力。介绍培养方案与课程设置。当前专业发 展热点等。 4 2 数学类专业课程介绍 了解每学期数学类课程的设置与地位;了解每门课 程的基本内容与作用。 4 3 计算机类课程介绍 了解每学期计算机类课程的设置与地位;了解每门 课程的基本内容与作用。 4 4 经验交流与大学四年规划 通过与优秀往届生的交流,认识到信计专业的优势 与特色,对专业未来的发展充满信心。大学四年规划 设想,进行 PPT 答辩。 4 五、说明 本课程与其他课程的关系 通过本课程的学习,学生掌握了课程模块的设置,为后期的专业课程选课打下坚实的基 础。六、学生成绩考核与评定方式 本课程考核方式为答辩,成绩由平时成绩和答辩成绩两部分构成,其中平时成绩占 30%, 答辩成绩占 70%

七、建议教材与参考书 建议教材:无 参考材料:网上文章。 八、课程中英文简介 通过本课程的学习,使学生了解信息与计算科学专业的内通,了解我校信息与计算科学 专业的发展史、发展现状、就业与考研、社会定位:掌握培养方案中的课程设置模块,了解 四年的开课计划,每门课程的基本内容与在专业设置中的地位:为大学生制定四年规划和设 定未来发展目标起若很大的指导作用。通过实践学习锻炼学生自主学习的能力。 The purpose of this course is to make students understand the nature of information and computing science,the development history of information and computing science in the University,future employment and social orientation,to master the couse module and the cours plan of four years,the basic content and the position of each course in the professional;It plays a great role in guiding the four years plan and future development for college students.In addition the ability of students toea independently through the practice 《离散数学》 课程编号 0BL09106 学分 4.5 总学时 72 实验/上机学时实验:0学时,上机:0学时 课程名称 离散数学 英文名称 Discrete Mathematics 课程类别 必修 适用专业 信息与计算科学 执笔人 左军 审核人 王爱文 先修课程 数学分析,高等代数 一、 课程的地位与作用 离散数学是现代数学的一个重要分支,是计算机科学与信息科学基础理论的重要课程, 它以研究离散量的结构和它们之间的关系为主要目标,其理论和方法在数学、自然科学和工 程技术中有若广泛的应用,其基本理论和研究成果全面而系统地影响和推动者计算机科学与 信息科学的发展。通过本课程的学习,使学生掌握离散数学的基本理论,掌握处理离散结构 所必需的描述工具和方法,并进一步培养抽象思维和严密推理的能力,并为学习后续专业课 程打下重要基础。 二、课程对应的毕业要求 使学生系统掌握离散数学的基本理论和研究方法,深入理解计算机科学与信息科学领域
12 七、建议教材与参考书 建议教材: 无 参考材料:网上文章。 八、课程中英文简介 通过本课程的学习,使学生了解信息与计算科学专业的内涵,了解我校信息与计算科学 专业的发展史、发展现状、就业与考研、社会定位;掌握培养方案中的课程设置模块,了解 四年的开课计划,每门课程的基本内容与在专业设置中的地位;为大学生制定四年规划和设 定未来发展目标起着很大的指导作用。通过实践学习锻炼学生自主学习的能力。 The purpose of this course is to make students understand the nature of information and computing science, the development history of information and computing science in the University, future employment and social orientation , to master the course module and the course plan of four years, the basic content and the position of each course in the professional; It plays a great role in guiding the four years plan and future development for college students. In addition, it can exercise the ability of students to learn independently through the practice. 《离散数学》 课程编号 0BL09106 学 分 4.5 总 学 时 72 实验/上机学时 实验:0 学时,上机:0 学时 课程名称 离散数学 英文名称 Discrete Mathematics 课程类别 必修 适用专业 信息与计算科学 执 笔 人 左军 审 核 人 王爱文 先修课程 数学分析,高等代数 一、课程的地位与作用 离散数学是现代数学的一个重要分支,是计算机科学与信息科学基础理论的重要课程, 它以研究离散量的结构和它们之间的关系为主要目标,其理论和方法在数学、自然科学和工 程技术中有着广泛的应用,其基本理论和研究成果全面而系统地影响和推动着计算机科学与 信息科学的发展。通过本课程的学习,使学生掌握离散数学的基本理论,掌握处理离散结构 所必需的描述工具和方法,并进一步培养抽象思维和严密推理的能力,并为学习后续专业课 程打下重要基础。 二、课程对应的毕业要求 使学生系统掌握离散数学的基本理论和研究方法,深入理解计算机科学与信息科学领域
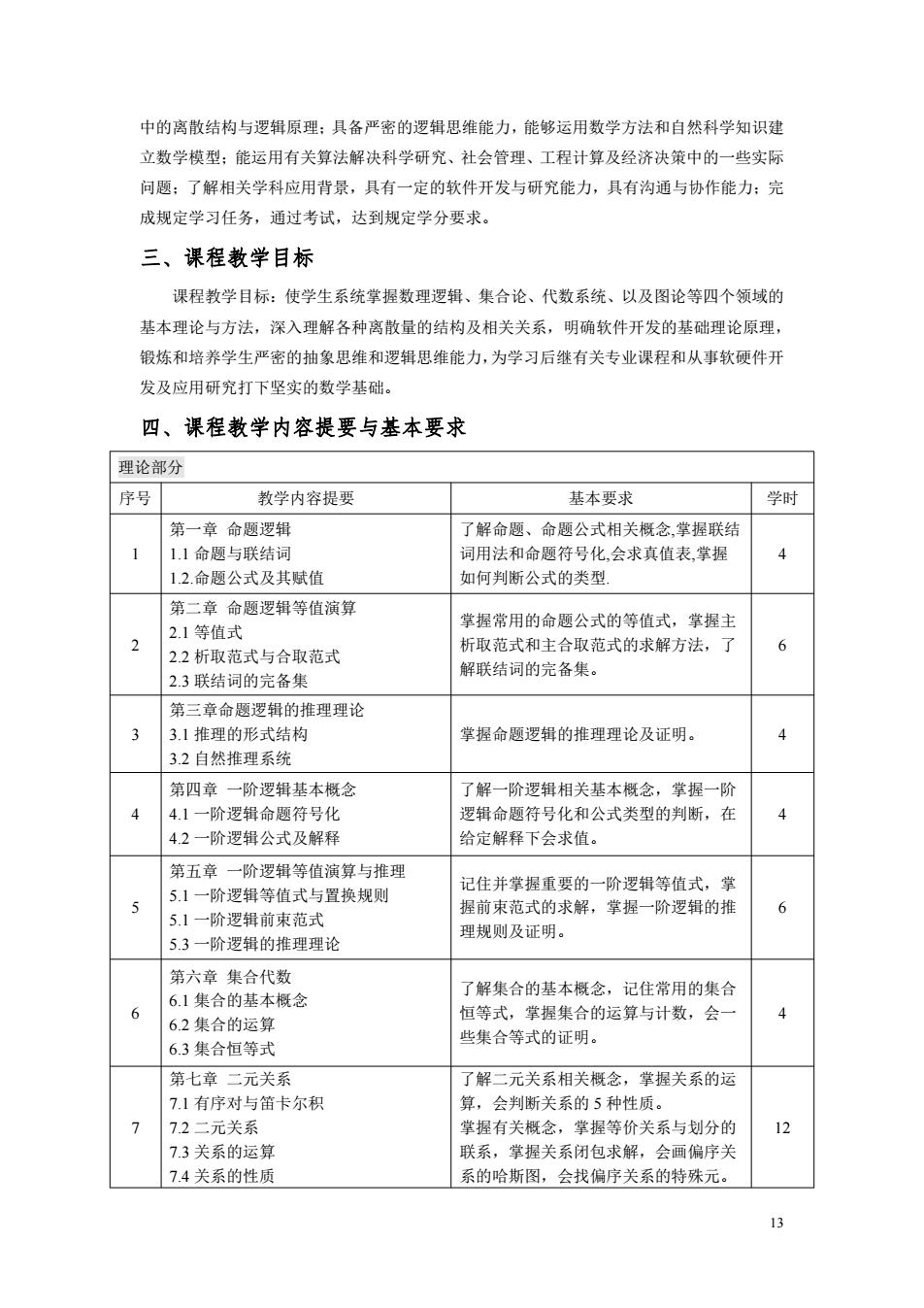
中的离散结构与逻辑原理:具备严密的逻辑思维能力,能够运用数学方法和自然科学知识建 立数学模型:能运用有关算法解决科学研究、社会管理、工程计算及经济决策中的一些实际 问题:了解相关学科应用背景,具有一定的软件开发与研究能力,具有沟通与协作能力:完 成规定学习任务,通过考试,达到规定学分要求。 三、课程教学目标 课程教学目标:使学生系统掌握数理逻辑、集合论、代数系统、以及图论等四个领域的 基本理论与方法,深入理解各种离散量的结构及相关关系,明确软件开发的基础理论原理, 锻炼和培养学生严密的抽象思维和逻辑思维能力,为学习后继有关专业课程和从事软硬件开 发及应用研究打下坚实的数学基础。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 第一章命题逻辑 解命题、命题公式相关概念,掌握联结 11命题与联结词 同用法和命题符号化,会求真值表掌握 4 12.命颗公式及其值 如何判断公式的类型. 第二章命题逻辑等值演算 掌握常用的命题公式的等值式,掌握主 2.1等值式 析取范式和主合取范式的求解方法,了 6 22析取范式与合取范式 解联结词的完备集。 23联结词的完备集 第三章命题逻辑的推理理论 3.1推理的形式结构 堂握命题罗辑的推理理论及证明。 4 32自然推理系统 第四意一阶罗辑基本概今 了解一阶罗辑相关基本概念,堂挥一阶 41一阶逻组命题符号化 逻辑命题符号化和公式类型的判断,在 4 4,2一阶逻辑公式及解释 给定解释下会求值 第五章一阶逻辑等值演算与推理 5. 阶逻辑等值式与置换规则 记住并掌握重要的 6 5.1一阶逻辑前束范式 理规则及证明。 5.3一阶逻辑的推理理论 第六章集合代数 了解集合的基本韬念,记住常用的集合 61集合的挂本概今 恒等式,掌握集合的运算与计数,会 4 62集合的运算 6.3集合恒等式 些集合等式的证明。 第七章二元关系 了解二元关系相关概念,掌握关系的运 7.1有序对与笛卡尔积 算,会判断关系的5种性质」 7 二元关系 掌握有关概念, 掌握等价关系与划分的 2 73关系的运算 联系, 掌捏关系闭包求解,会画偏序关 7.4关系的性质 系的哈斯图,会找偏序关系的特殊元
13 中的离散结构与逻辑原理;具备严密的逻辑思维能力,能够运用数学方法和自然科学知识建 立数学模型;能运用有关算法解决科学研究、社会管理、工程计算及经济决策中的一些实际 问题;了解相关学科应用背景,具有一定的软件开发与研究能力,具有沟通与协作能力;完 成规定学习任务,通过考试,达到规定学分要求。 三、课程教学目标 课程教学目标:使学生系统掌握数理逻辑、集合论、代数系统、以及图论等四个领域的 基本理论与方法,深入理解各种离散量的结构及相关关系,明确软件开发的基础理论原理, 锻炼和培养学生严密的抽象思维和逻辑思维能力,为学习后继有关专业课程和从事软硬件开 发及应用研究打下坚实的数学基础。 四、课程教学内容提要与基本要求 理论部分 序号 教学内容提要 基本要求 学时 1 第一章 命题逻辑 1.1 命题与联结词 1.2.命题公式及其赋值 了解命题、命题公式相关概念,掌握联结 词用法和命题符号化,会求真值表,掌握 如何判断公式的类型. 4 2 第二章 命题逻辑等值演算 2.1 等值式 2.2 析取范式与合取范式 2.3 联结词的完备集 掌握常用的命题公式的等值式,掌握主 析取范式和主合取范式的求解方法,了 解联结词的完备集。 6 3 第三章命题逻辑的推理理论 3.1 推理的形式结构 3.2 自然推理系统 掌握命题逻辑的推理理论及证明。 4 4 第四章 一阶逻辑基本概念 4.1 一阶逻辑命题符号化 4.2 一阶逻辑公式及解释 了解一阶逻辑相关基本概念,掌握一阶 逻辑命题符号化和公式类型的判断,在 给定解释下会求值。 4 5 第五章 一阶逻辑等值演算与推理 5.1 一阶逻辑等值式与置换规则 5.1 一阶逻辑前束范式 5.3 一阶逻辑的推理理论 记住并掌握重要的一阶逻辑等值式,掌 握前束范式的求解,掌握一阶逻辑的推 理规则及证明。 6 6 第六章 集合代数 6.1 集合的基本概念 6.2 集合的运算 6.3 集合恒等式 了解集合的基本概念,记住常用的集合 恒等式,掌握集合的运算与计数,会一 些集合等式的证明。 4 7 第七章 二元关系 7.1 有序对与笛卡尔积 7.2 二元关系 7.3 关系的运算 7.4 关系的性质 了解二元关系相关概念,掌握关系的运 算,会判断关系的 5 种性质。 掌握有关概念,掌握等价关系与划分的 联系,掌握关系闭包求解,会画偏序关 系的哈斯图,会找偏序关系的特殊元。 12
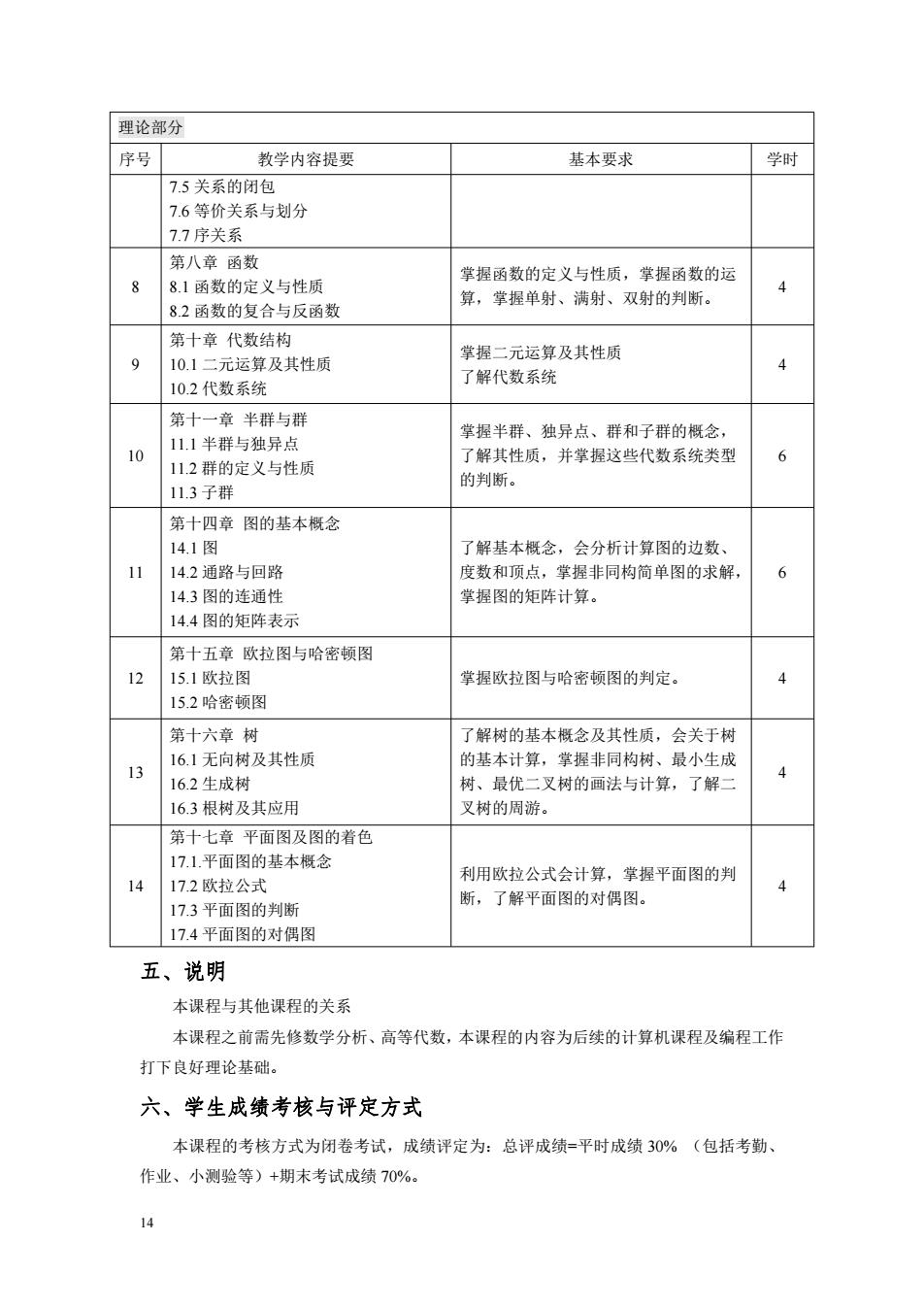
理论部分 序号 教学内容提要 基本要求 学时 7.5关系的闭包 76等价关系与划分 7.7序关系 第八章函数 8.1函数的定义与性质 掌握函数的定义与性质,掌握函数的运 82函数的复合与反函数 算,掌握单射、满射、双射的判断。 第十章代数结构 掌握二元运算及其性质 9 10.1 二元运算及其性质 了解代数系统 10.2代数系统 第十一章半群与群 掌握半群、独异点、群和子群的概念, 111半群与独异点 了解其性质,并掌握这些代数系统类型 6 112群的定义与性质 的判断。 11.3子群 第十四章图的基本概念 1A1四 了解基本概念,会分析计算图的边数、 11 142通路与回路 度数和顶点。 握非同构简单图的求解 6 14.3图的连通性 掌握图的矩阵计算。 14.4图的矩阵表示 第十五章欧拉图与哈密顿图 151欢拉图 掌握欧拉图与哈密顿图的判定。 4 152哈密顿图 第十六意树 了解树的基本概念及其性质,会关于树 16.1无向树及其性质 13 的基本计算,掌握非同构树、最小生成 16.2 最优 叉树的画法与计算 了解 16.3根树及其应用 叉树的周游。 第十七章平面图及图的着色 17.1.平面图的基本概念 利用欧拉公式会计算,掌握平面图的判 172欧拉公式 4 17.3平面图的判断 断,了解平面图的对偶图。 17.4平面图的对偶图 五、说明 本课程与其他课程的关系 本课程之前需先修数学分析、高等代数,本课程的内容为后续的计算机课程及编程工作 打下良好理论基础。 六、学生成绩考核与评定方式 本课程的考核方式为闭卷考试,成锁评定为:总评成绩=平时成绩30%(包括考勤、 作业、小测验等)+期末考试成绩70%。 14
14 理论部分 序号 教学内容提要 基本要求 学时 7.5 关系的闭包 7.6 等价关系与划分 7.7 序关系 8 第八章 函数 8.1 函数的定义与性质 8.2 函数的复合与反函数 掌握函数的定义与性质,掌握函数的运 算,掌握单射、满射、双射的判断。 4 9 第十章 代数结构 10.1 二元运算及其性质 10.2 代数系统 掌握二元运算及其性质 了解代数系统 4 10 第十一章 半群与群 11.1 半群与独异点 11.2 群的定义与性质 11.3 子群 掌握半群、独异点、群和子群的概念, 了解其性质,并掌握这些代数系统类型 的判断。 6 11 第十四章 图的基本概念 14.1 图 14.2 通路与回路 14.3 图的连通性 14.4 图的矩阵表示 了解基本概念,会分析计算图的边数、 度数和顶点,掌握非同构简单图的求解, 掌握图的矩阵计算。 6 12 第十五章 欧拉图与哈密顿图 15.1 欧拉图 15.2 哈密顿图 掌握欧拉图与哈密顿图的判定。 4 13 第十六章 树 16.1 无向树及其性质 16.2 生成树 16.3 根树及其应用 了解树的基本概念及其性质,会关于树 的基本计算,掌握非同构树、最小生成 树、最优二叉树的画法与计算,了解二 叉树的周游。 4 14 第十七章 平面图及图的着色 17.1.平面图的基本概念 17.2 欧拉公式 17.3 平面图的判断 17.4 平面图的对偶图 利用欧拉公式会计算,掌握平面图的判 断,了解平面图的对偶图。 4 五、说明 本课程与其他课程的关系 本课程之前需先修数学分析、高等代数,本课程的内容为后续的计算机课程及编程工作 打下良好理论基础。 六、学生成绩考核与评定方式 本课程的考核方式为闭卷考试,成绩评定为:总评成绩=平时成绩 30% (包括考勤、 作业、小测验等)+期末考试成绩 70%

七、建议教材与参考书 建议教材:耿素云屈婉玲编著,离散数学,高等教育出版社,2004.1第2版, 参考书:1.耿素云屈婉玲张立昂编著,离散数学,清华大学出版社20043第3版 2.左孝凌等编著,离散数学,上海科学技术文献出版社,1982.9第1版 八、课程中英文简介 离散数学是现代数学的一个重要分支,是计算机科学与信息科学理论的重要基础课程, 其理论和方法在数学、自然科学和工程技术中有着广泛的应用。通过本课程的学习使学生不 仅获得基本理论知识,而且培养抽象思维和逻辑推理能力。使学生能够运用数学方法和白然 科学知识建立数学模型,能运用有关算法解决科学研究、社会管理、工程计算及经济决策中 的一些实际问题。本课程的基本内容包括数理逻辑、集合论、代数系统、以及图论等四个领 域的基本理论与方法。本课程也为学生学习后继有关专业课程和从事软硬件开发及应用研究 打下坚实的数学基础 Discrete mathematics is an important branch of modem mathematics,It is important basic course of computer science and information science theory.Its theory and methods have a broad application in mathematics,natural science and engineering technology.Learning this course makes students not only get the basic theoretical knowledge,but also Train the ability of abstract thinking and logical reasoning Students can use mathematical methods and natural science knowledge to build mathematical model,can use the algorithm to solve the scientific research, social management engineering calculation.and some practical problems in economic decision-making The basic content of the course includes basic theory and method of the following four areas of mathematical logic,set theory,algebra and graph theory.Through the course,This course is for students to leam the subsequent relevant professional courses and engaged in the development and application of software and hardware to lay a solid mathematica foundation 《常微分方程》 课程编号 0BL09107 学分 3 总学时 48 实验/上机学时实验:0学时,上机:0学时 课程名称 常微分方程 英文名称 Ordinary Differential Equations 课程类别 必修 适用专业 信息与计算科学、应用统计学 执笔人 王爱文 审核人 黄静静 先修课程 数学分析、高等代数
15 七、建议教材与参考书 建议教材:耿素云 屈婉玲编著,离散数学, 高等教育出版社 ,2004.1 第 2 版. 参考书: 1. 耿素云 屈婉玲 张立昂编著,离散数学,清华大学出版社,2004.3 第 3 版. 2. 左孝凌 等编著,离散数学,,上海科学技术文献出版社,1982.9 第 1 版. 八、课程中英文简介 离散数学是现代数学的一个重要分支,是计算机科学与信息科学理论的重要基础课程, 其理论和方法在数学、自然科学和工程技术中有着广泛的应用。通过本课程的学习使学生不 仅获得基本理论知识,而且培养抽象思维和逻辑推理能力。使学生能够运用数学方法和自然 科学知识建立数学模型,能运用有关算法解决科学研究、社会管理、工程计算及经济决策中 的一些实际问题。本课程的基本内容包括数理逻辑、集合论、代数系统、以及图论等四个领 域的基本理论与方法。本课程也为学生学习后继有关专业课程和从事软硬件开发及应用研究 打下坚实的数学基础 Discrete mathematics is an important branch of modern mathematics, It is important basic course of computer science and information science theory. Its theory and methods have a broad application in mathematics, natural science and engineering technology. Learning this course makes students not only get the basic theoretical knowledge, but also Train the ability of abstract thinking and logical reasoning. Students can use mathematical methods and natural science knowledge to build mathematical model, can use the algorithm to solve the scientific research, social management, engineering calculation, and some practical problems in economic decision-making. The basic content of the course includes basic theory and method of the following four areas of mathematical logic, set theory, algebra and graph theory. Through the course, This course is for students to learn the subsequent relevant professional courses and engaged in the development and application of software and hardware to lay a solid mathematical foundation. 《常微分方程》 课程编号 0BL09107 学 分 3 总 学 时 48 实验/上机学时 实验:0 学时,上机:0 学时 课程名称 常微分方程 英文名称 Ordinary Differential Equations 课程类别 必修 适用专业 信息与计算科学、应用统计学 执 笔 人 王爱文 审 核 人 黄静静 先修课程 数学分析、高等代数